Главная | Обратная связь | Поможем написать вашу работу!

1.1 Второе начало термодинамики

1. 1 Второе начало термодинамики

Одной из важнейших задач химической термодинамики является выяснение принципиальной возможности (или невозможности) самопроизвольного протекания химической реакции в рассматриваемом направлении. В тех случаях, когда становится ясно, что данное химическое взаимодействие происходить может, необходимо определить степень превращения исходных веществ и выход продуктов реакции, то есть полноту протекания реакции

Направление протекания самопроизвольного процесса можно определить на основе второго закона или начала термодинамики, сформулированного, например, в виде постулата Клаузиуса:

Теплота сама собой не может переходить от холодного тела к горячему, т. е. невозможен такой процесс, единственным результатом которого был бы переход теплоты от тела с более низкой температурой к телу с более высокой температурой.

Предложено множество формулировок второго начала термодинамики. Формулировка Томсона - Планка:

Невозможен вечный двигатель второго рода, т. е. невозможна такая периодически действующая машина, которая бы позволяла получать работу только за счет охлаждения источника тепла.

Математическая формулировка второго начала термодинамики возникла при анализе работы тепловых машин в трудах Н. Карно и Р. Клаузиуса.

Клаузиусом была введена функция состояния S, названная энтропией, изменение которой равно теплоте обратимого процесса, отнесенной к температуре

(1. 21)

Так как теплота необратимого процесса меньше теплоты обратимого процесса

(1. 21а)

Для любого процесса

(1. 22)

Полученное выражение представляет собой математическое выражение второго начала термодинамики.

Изменение энтропии при нагревании

В изобарных условиях (p = const) теплота процесса равна изменению энтальпии, тогда

(1. 23)

Изменение энтропии при нагревании от температуры T₁ до температуры T₂:

(1. 24)

Если использовать средние теплоемкости в интервале температур от T₁ до T₂, то изменение энтропии при нагревании, может быть рассчитано как

(1. 25)

Так как T₂> T₁, то Δ S > 0, т. е. при нагревании энтропия возрастает. Это соответствует физическому смыслу энтропии, так как при повышении температуры скорость хаотичного движения молекул возрастает.

1. 4 Расчет изменения энтропии и энергии Гиббса в химических процессах

Поскольку энтропия является функцией состояния, то изменение энтропии в ходе химической реакции можно рассчитать как разность сумм энтропий продуктов реакции (конечных веществ) и реагентов (исходных веществ):

(1. 26)

Пользуясь значениями стандартных энтропий веществ, изменение энтропии при протекании химической реакции в стандартных условиях можно рассчитать по формуле:

(1. 27)

Изменение энтропии при химическом превращении при любой температуре T и стандартном давлении можно рассчитать исходя из зависимости энтропии каждого вещества, участвующего в реакции, от температуры. С использованием средних теплоемкостей изменение энтропии системы при протекании в ней химической реакции рассчитывается по уравнению:

(1. 28)

Пример: Рассчитаем изменение энтропии для реакции синтеза метанола при стандартных условиях.

Решение: Для расчетов воспользуемся справочными значениями стандартных энтропий, участвующих в реакции веществ (см. табл. 44 на стр. 72 справочника [2]).

Стандартная энтропия	СО_{(Г. )}	+ 2 Н_{2 (г. )}	= СН₃ОН_{(г. )}
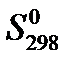, Дж/(моль∙ К)	197, 55	130, 52	239, 76

Изменение энтропии при протекании химической реакции в стандартных условиях равно:

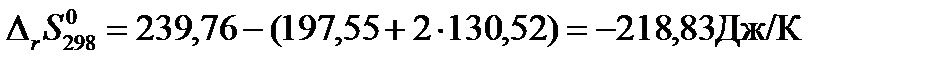
Пример: Рассчитаем изменение энтропии для реакции синтеза метанола при температуре 1000 К.

Решение: Для расчетов воспользуемся рассчитанным в примере 2 значением изменения средней теплоемкости системы за счет протекания в ней химической реакции в интервале температур от 298 до 1000К 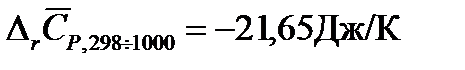. Тогда Изменение энтропии для данной реакции при 1000К будет равно:

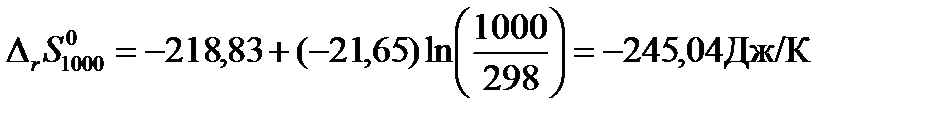
В соответствии с первым и вторым началами термодинамики для обратимого процесса можем записать

(1. 28)

или

(1. 29)

где – максимальная полезная работа обратимого процесса, которая включает все виды работ, кроме работы расширения газа.

Это выражение называется объединённым уравнением первого и второго начал термодинамики, из него следует, что

или по свойствам дифференциалов:

Обозначив разность (H – TS) как G и получим

(1. 30)

Таким образом, максимальная полезная работа в изобарно-изотермических условиях равна изменению термодинамической функции, которая получила название энергия Гиббса (изобарно-изотермический потенциал) и условно обозначается буквой G.

Для изохорно-изотермических условий (V = const, p = const) dV = 0, поэтому

(1. 31)

Таким образом, максимальная полезная работа в изохорно-изотермических условиях равна изменению термодинамической функции, которая получила название энергия Гельмгольца (изохорно-изотермический потенциал) и условно обозначается буквой A.

Большинство процессов в химико-технологических системах протекают в изобарно-изотермических условиях, для которых максимально полезная работа в ходе обратимого процесса равна убыли энергии Гиббса:

(1. 30а)

Энергия Гиббса является функцией состояния. Изменение энергии Гиббса представляет собой ту часть полной энергии системы, которую в принципе можно превратить в максимальную полезную работу и является суммарной движущей силой процесса в изобарно-изотермических условиях.

В необратимых процессах работа всегда меньше, чем в обратимых. Тогда для необратимого и самопроизвольного процесса справедливо неравенство

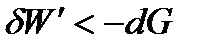(1. 32)

или для конечного процесса

(1. 32а)

Изменение энергии Гиббса в конечном процессе можно рассчитать как

(1. 33)

откуда

(1. 34)

Это выражение также является математическим выражением второго начала термодинамики. Из него следует, что теплота процесса (Δ H) может быть лишь частично превращена в работу, которую характеризует свободная энергия Гиббса (Δ G). Функция TΔ S – тепло, которое не может быть превращено в работу, TΔ S называется связанной энергией.

Изменение стандартной энергии Гиббса при протекании реакции при любой температуре, в соответствии со вторым началом термодинамики, рассчитывается по уравнению:

(1. 35)

Пример: Рассчитаем изменение стандартной энергии Гиббса для реакции синтеза метанола при температуре 1000К.

Р ешение: Для расчетов воспользуемся рассчитанными в предыдущих примерах при температуре 1000К значениями теплового эффекта реакции синтеза метанола и изменения энтропии системы за счет протекания в ней химической реакции . Тогда изменение стандартной свободной энергии Гиббса для данной реакции при 1000К будет равно:

⇐ Предыдущая 1 2 3 456 7 8 9 10 Следующая ⇒

Воспользуйтесь поиском по сайту: