 |
Практические константы равновесия
|
|
|
|
Практические константы равновесия
Химическое равновесие могут характеризовать практические константы равновесия. Практические константы равновесия могут быть рассчитаны, если при равновесии определить количества или концентрации веществ, участвующих в реакции тем или иным методом химического или физико-химического анализа. Они могут быть выражены
– через числа молей веществ ni, j в равновесии:
 ; ;
| (1. 12) |
– через молярные концентрации веществ сi, j в равновесии:
 ; ;
| (1. 13) |
– через мольные доли веществ xi, j в равновесии:
 ; ;
| (1. 14) |
– через парциальные давления веществ pi, j в равновесии:

| (1. 15) |
Практические константы равновесия являются размерными величинами.
Удобно использовать и безразмерные константы равновесия, например, константу, выраженную через приведенные давления  :
:
 , ,
| (1. 16) |
где  , а p0 – стандартное давление.
, а p0 – стандартное давление.
Между практическими константами равновесия существует определенная математическая связь. Например, легко показать, что константа 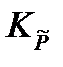 связана с практической константой равновесия, выраженной через моли Kn, следующим соотношением
связана с практической константой равновесия, выраженной через моли Kn, следующим соотношением
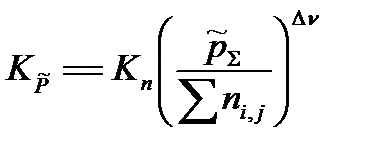
| (1. 17) |
1. 7 Расчет степени превращения исходных веществ, выхода продукта и равновесного состава химической реакции
Для расчета равновесного состава была введена универсальная величина – химическая переменная или глубина превращения ξ (кси), равная отношению изменения количества вещества данного реагента или продукта реакции к его стехиометрическому коэффициенту в уравнении химической реакции:
 , ,
| (1. 18) |
|
|
|
где знак “+” используется для продуктов реакции, а знак “ – “ для исходных веществ.
Равновесное количество вещества для каждого участника реакции выразим через глубину превращения:

| (1. 19) |
Подставив полученное выражение в уравнение, связывающее термодинамическую Ka =  и практическую Kn константы равновесия, получим
и практическую Kn константы равновесия, получим

| (1. 20) |
Решив это уравнение относительно химической переменной ξ, можно рассчитать: равновесные количества вещества каждого участника реакции, равновесные концентрации реагентов, степень превращения исходных веществ и выход продуктов реакции.
Пример: Определим равновесную глубину превращения ξ в реакции 2CO + S2 = 2COS при температуре 500 К и давлении 101, 013 кПа., при условии, что исходные вещества взяты в стехиометрических количествах. Константа равновесия  = 3, 56·1011.
= 3, 56·1011.
Решение: Выразим равновесный состав через химическую переменную ξ и найдем область допустимых значений (ОДЗ) ξ из условия, число молей вещества всегда положительная величина:
| 2CO | + S2 = | 2COS | |
исх. состав
n0, i  , моль , моль
| |||
равн. состав
n 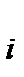 , моль , моль
|
2–2 
|
1– 
|
2 
|
| ОДЗ ξ: | ||
2–2  > 0 > 0
|
| |
1–  > 0 > 0
| => 0 <  < 1 < 1
| |
2  > 0 > 0
|
Выразим практическую константу Kn через глубину превращения ξ:

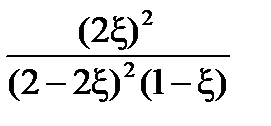
Выразим сумму молей газообразных веществ в равновесии через глубину превращения ξ:
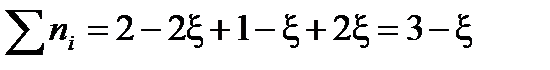
Найдем разность стехиометрических коэффициентов в уравнении реакции:

Подставим Kn,  и
и  в уравнение, связывающее термодинамическую константу
в уравнение, связывающее термодинамическую константу  с практической константой Kn
с практической константой Kn
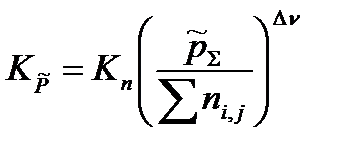
 =
=
=  =
= 
Полученное кубическое уравнение
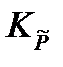 =
= 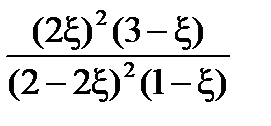
решаем точно, отбирая корни в соответствии с областью допустимых значений ξ, или приближенно (методом подбора или графически), что для практических расчетов вполне допустимо. Используя метод приближенных вычислений, получим при  = 3, 56·1011
= 3, 56·1011  = 0, 9998.
= 0, 9998.
|
|
|
Пример: Определим равновесную глубину превращения ξ в реакции 2CO + S2 = 2COS при температуре 500 К и давлении 101, 013 кПа., при условии, что исходный состав содержал 0, 2 моля СО и 2 моля газообразной серы. Константа равновесия  = 3, 56·1011.
= 3, 56·1011.
Решение: Выразим равновесный состав через химическую переменную ξ и найдем область допустимых значений (ОДЗ) ξ:
| 2CO | + S2 = | 2COS | |
исх. состав
n  , моль , моль
| 0, 2 | ||
равн. состав
n 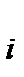 , моль , моль
|
0, 2–2 
|
2– 
|
2 
|
| ОДЗ ξ: | ||
0, 2–2  > 0 > 0
|
| |
2–  > 0 > 0
| => 0 <  < 0, 1 < 0, 1
| |
2  > 0 > 0
|
Выразим практическую константу Kn через глубину превращения ξ:

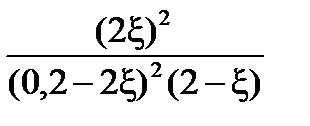
Выразим сумму молей газообразных веществ в равновесии через глубину превращения ξ:
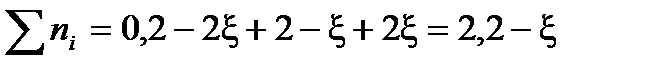
Найдем разность стехиометрических коэффициентов в уравнении реакции:

Подставим Kn,  и
и  в уравнение, связывающее термодинамическую константу
в уравнение, связывающее термодинамическую константу  с практической константой Kn
с практической константой Kn
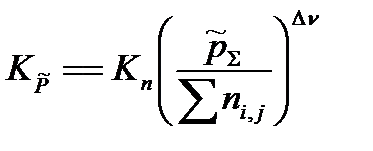
 =
=
= 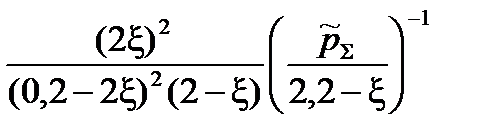 =
= 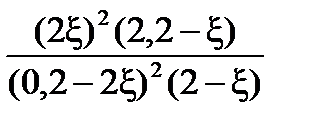
Полученное кубическое уравнение
 =
= 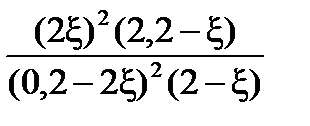
решаем приближенно и получаем при  = 3, 56·1011
= 3, 56·1011  = 0, 0999997.
= 0, 0999997.
Пример: Определим степень превращения исходных веществ в реакции
2CO + S2 = 2COS
при условиях предыдущих примеров.
Решение:
Степень превращения β i – это отношение количества прореагировавшего вещества к его начальному количеству:
β i =  = = 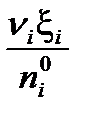
| ((1. 21) |
При условии примера, в котором исходные вещества взяты в стехиометрических количествах, с  = 0, 9998:
= 0, 9998:
β  = 99, 98 %
= 99, 98 %
β 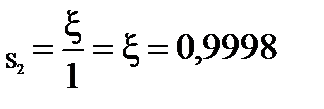 =99, 98 %
=99, 98 %
При условии примера, в котором исходный состав содержал 0, 2 моля СО и 2 моля газообразной серы, с  = 0, 0999997
= 0, 0999997
β  000 = 50, 00 %
000 = 50, 00 %
β 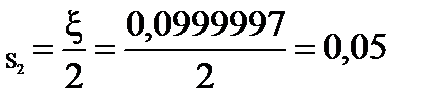 00 = 5, 00 %
00 = 5, 00 %
Пример: Определим состав равновесной смеси в % (мол. ) для реакции
2CO + S2 = 2COS
при условиях предыдущих примеров.
Решение:
Мольная доля вещества в смеси равна:

| ((1. 22) |
или в % (мол):
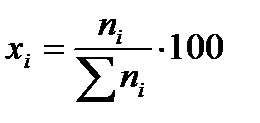
При условии примера, в котором исходные вещества взяты в стехиометрических количествах, с  = 0, 9998
= 0, 9998
 (мол. )
(мол. )
 (мол. )
(мол. )
 (мол. )
(мол. )
При условии примера, в котором исходный состав содержал 0, 2 моля СО и 2 моля газообразной серы, с  = 0, 0999997
= 0, 0999997
|
|
|
 (мол. )
(мол. )
 (мол. )
(мол. )
 (мол. )
(мол. )
|
|
|


