Управление точностью обработки по выходным данным.

Второй путь управления заключается в том, что поправка динамической настройки D_д, необходимая для компенсации отклонения размера динамической настройки А_д, вносится за счет изменения последнего. Величина размера динамической настройки А_д зависит от силы резания и жесткости системы. Следовательно, при заданной жесткости управлять величиной А_д можно, изменяя силу резания Р. Для изменения силы резания можно использовать любой из факторов, от изменения которого зависит величина и направление этой силы. Из анализа формулы:

или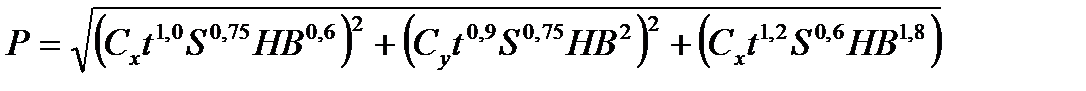

 

следует, что для управления силы резания можно воспользоваться изменением величины:

4) продольной подачи;

5) твердости материалов заготовки;

6) коэффициентов С_z; С_y; С_x; характеризующих условие обработки, т.е. геометрию инструмента, скорость резания и т.д.. Следовательно управлять силой резания можно также путем изменения скорости резания u и геометрии режущего инструмента. Изменять твердость материала в процессе обработки деталей с необходимой твердостью в требуемых пределах пока не представляется возможным.

Проще всего уменьшать поле рассеяния твердостью, припусков сортируя заготовки, но это очень трудоемко.

Поэтому, при заданной геометрии режущего инструмента и выбранной скорости резания (исходя из стойкости режущего инструмента) достаточно эффективно силой резания можно управлять изменением продольной подачи. Основным преимуществом использования подачи, в качестве параметра управления силой резания является возможность создание очень тонкого и чувствительного механизма управления упругими перемещениями системы СПИД, не имеющего никаких скачков. В соответствии с этим размер статической настройки А_с остается неизменным в течении всего времени обработки деталей между двумя поднастройками, необходимыми для компенсации размерного износа режущего инструмента и осуществляемыми с помощью механизма активного контроля.

Управление подачей может осуществляться рабочим в ручную или с помощью системы автоматического управления (САУ). Подача может изменяться дискретно или еще лучше непрерывно и автоматически.

При ручном изменении подачи рабочий наблюдает за отклонением стрелки прибора и вносит новые изменения в величину подачи, пока стрелка не возвращается в исходное положение. При автоматическом управлении подачи эти функции выполняет САУ. При обработке детали с большой величиной припуска и твердости рабочий или САУ соответственно уменьшают величину подачи, при обработке следующей детали с меньшей величиной припуска на обработку увеличивают подачу и т.д.

Регулирование подачи в процессе обработки заготовок дает возможность не только уменьшать, но и повышать точность геометрической формы заготовок. В процессе обработки заготовок на токарных и шлифовальных станках жесткость технологической системы не остается постоянной в связи с различной податливостью самой обрабатываемой заготовки по длине ее. Для получения правильной геометрической формы обрабатываемой заготовки необходимо компенсировать не только колебание силы резания вызванное не постоянством НВ, Z_min, но и упругие отжатия технологической системы. Т.е. необходимо создать дополнительное устройство, которое обеспечивало бы точность геометрической формы заготовки по ее длине. На станках с ЧПУ подобные изменения продольной подачи по длине обработки заготовки должны быть внесены в управляющую программу.

Результаты обработки партии чугунных деталей (по данным Каф. ТМ Станкина под руководством профессора Б.С. Балакшина) дали следующие показатели: величина поля рассеяния w_т = 0,061 мм при обычной обработке сократилось до w^¢_т =0,027 мм при использовании САУ. Поле рассеяния погрешности формы детали в продольном сечении с w_т =0,042/300 сократилось до w^¢_т=0,012/300 с использованием САУ.

Т.е. управление упругими перемещениями продольной подачи позволяет:

5) Существенно повысить точность обработки заготовок и других показателей качества за счет уменьшения поля рассеяния, порождаемого совокупным действием факторов;

6) Увеличить штучную производительность подавляющего большинства технологических систем (рост производительности обработки за счет применения наивысших режимов резания, допускаемых данной технологической системой при заданной точности);

7) Использовать чрезвычайно тонкий и чувствительный механизм регулирования технологической системы, работающей без скачков, с сохранением постоянного размера А_с;

8) Обеспечить обработку заготовок с равномерной нагрузкой технологической системы, что способствует более экономичному использованию оборудования и режущего инструмента.

Недостаток: изменение подачи увеличивает шероховатость обрабатываемой поверхности. С увеличением подачи шероховатость увеличивается, т.е. шероховатость, вследствие колебания S, становится неоднородной. Во многих случаях этот недостаток не является существенным, т.к. после обычных операций проводят более тонкую доводочную обработку.

Системы САУ нашли применение в ряде конструкций станков (с ЧПУ, управляемых микроЭВМ и микропроцессорами). Наиболее целесообразно – одноинструментная обработка. Недостаток – дороговизна.

Факторы, влияющие на качество поверхности (R_z от V, R_z от S, глубина резания, форма режущей кромки, механические свойства химический состав и структура материала заготовки, СОЖ, жесткость, вибрации, остаточные напряжения). Шероховатость поверхностей заготовок возникает от воздействия ряда факторов в процессе их получения. Заготовки из проката имеют следы шероховатостей прокатных валков. Высота неровностей горячекатаного проката не превышает 150 мкм, а холоднотянутого 50 мкм. Заготовки, полученные свободной ковкой, в зависимости от размера имеют неровности поверхности 1,5¸4 мкм. У горяче-штампованных заготовок на поверхности остаются следы окалины и воспроизводятся поверхностные погрешности штампов. В зависимости от размера заготовок и состояния штампов высота неровностей 150-500мм. Шероховатость отливок зависит от шероховатости стенок литейных форм, величины зерен формовочной смеси, плотности ее набивки и др. факторов. При литье в песчаные формы ручной формовки мелких заготовок неровности достигают 500 мкм, при литье крупных заготовок 1500 мкм. При машинной формовке – 300 мкм; при кокильном и центробежном литье – 200 мкм; при литье под давлением 10 мкм; при литье по выплавляемым моделям и в корковые формы 10¸40 мкм.

Поверхностный слой заготовок, полученных ковкой, горячей штамповкой и прокаткой, горячей штамповкой и прокаткой, состоит из обезуглероженной зоны и переходит в зону, в которой наблюдается частичное обезуглероживание. Глубина обезуглероженного слоя у заготовок, полученных свободной ковкой, 500-1000 мкм; у проката до 150 мкм и у калиброванного проката до 50 мкм. Отливки из серого чугуна имеют перлитную корку (перлитная зона) на глубину 300 мкм и за ней зону со значительным содержанием феррита, переходящего постепенно в основную зону.

Поверхностный слой стальных отливок имеет зону обезуглероживания до 200 мкм и далее переходную зону с частичным обезуглероживанием.

При обработке заготовок резанием шероховатость измеренная в направлении движения подачи (поперечная шероховатость), обычно больше шероховатости, измеренной в направлении главного движения режущего инструмента (продольная шероховатость). На шероховатость влияет ряд факторов.

Режимы резания оказывают заметное влияние на шероховатость обрабатываемой поверхности. Наибольшее влияние оказывает скорость резания, с увеличением которой до значения 20-25 м/мин высота микронеровностей достигает наибольшего значения. При дальнейшем увеличении, при прочих неизменных условиях, шероховатость постепенно уменьшается. Зона увеличенной шероховатости связана с образованием нароста на режущей кромке инструмента. С увеличением скорости наростообразование прекращается и шероховатость уменьшается, что очень хорошо заметно при обработке стали.

Влияние подачи на шероховатость поверхности при разных методах обработки сказывается по разному. При точении стандартными проходными резцами с углом в плане 45° и малым радиусом закругления вершины (2 мм) влияние подачи весьма заметно. При точении резцами с широкой режущей кромкой влияние подачи практически отсутствует, что позволяет повысить производительность обработки отделочных операций. Умеренное влияние подачи на шероховатость поверхности отверстий, торцовом и цилиндрическом фрезеровании и других методах обработки.

Глубина резания не оказывает заметного влияния на шероховатость, если жесткость технологической системы достаточно велика. В некоторых случаях (снятие литейной корки или удаление наклепанного слоя) увеличение глубины резания уменьшает шероховатость поверхности, т.к. инструмент работает по основному металлу.

Форма режущей кромки инструмента также влияет на шероховатость поверхности. При шлифовании шероховатость снижается с увеличением окружной скорости шлифовального круга, уменьшением скорости вращения заготовки, размеров зерна круга и глубины шлифования. Шлифование с выхаживанием повышает чистоту обработки.

На шероховатость поверхности влияют механические свойства, химический состав и структура материала заготовок. При обработке заготовок из мягкой низкоуглеродистой стали получается более шероховатая поверхность, чем при обработке заготовок из твердой стали с большим содержанием углерода. Заготовки из стали с повышенным содержанием серы (автоматные стали) и из стали с присадкой свинца имеют более чистую поверхность среза, чем заготовки из обычных сталей. Заготовки из сталей с мелкозернистой структурой обрабатываются лучше заготовок с крупнозернистой структурой.

На полученную при обработке шероховатость поверхности оказывает существенное влияние жесткость технологической системы. Непостоянство жесткости в разных сечениях заготовки, обусловленное условиями ее закрепления вызывает неоднородность шероховатости обработанной поверхности. Вибрации элементов технологической системы периодически изменяют положение режущей кромки инструмента относительно обрабатываемой поверхности, создавая на ней выступы и впадины. На процесс вибрации влияют жесткость системы, зазоры в ее звеньях, неуравновешенность вращающихся частей, дефекты приводов и др. При относительно невысокой частоте и большой амплитуды колебаний на обрабатываемой поверхности образуется волнистость. Зная влияние технологических факторов на шероховатость поверхности, можно создавать условия обработки, обеспечивающие достижение заданной шероховатости поверхности. При чистовой и черновой обработке стали, деформация распространяется на глубину от 50 до 100-300 мкм, а при обдирке до 500¸1000.

Снять остаточные напряжения после предварительного шлифования можно отжигом детали, а после ее окончательной обработки – виброконтактным полированием. При обработке этим методом на поверхности образуются сжимающие напряжения. Вообще, управление остаточными напряжениями – важный резерв повышения эксплуатационных свойств деталей машин. Увеличение S увеличивает остаточные напряжения растяжения и вызывает рост пластической деформации поверхностного слоя.

Износ и затупление инструмента приводит к повышению трения по его задней поверхности об обрабатываемую поверхность, это способствует формированию остаточных напряжений растяжения при относительно большой глубине их распространения.

При обработке в электролите (электрохимическая обработка) поверхностный слой насыщается водородом, что может привести к хрупкой поломке деталей. Для устранения этого недостатка, а также для уменьшения остаточных напряжений, образующихся в поверхностном слое при изготовлении ответственных деталей (турбинные лопатки), нередко применяется дополнительное механическое полирование. Водород можно удалить отпуском детали при температуре 120-140°С.

Случайные погрешности обработки. Кривые распределения и оценка точности обработки (полигон распределения, законы Гаусса, равной вероятности, Симпсона, Релея). Точечные диаграммы и их применение для исследования точности обработки. Случайные погрешности – это погрешность, которая для разных заготовок рассматриваемой партии имеет различные значения, причем ее появление не подчиняется никакой видимой закономерности. В результате возникновения случайных погрешностей происходит рассеяние размеров заготовок, обработанных при одних и тех же условиях. Рассеяние размеров вызвано совокупностью многих случайных причин: колебание твердости обрабатываемого материала и величины снимаемого припуска; изменения положение заготовки в приспособлениях, связанное с погрешностью ее базирования и закрепления или обусловленные неточностью приспособления; неточность установки положения суппортов по упорам и лимбам; т.д. Для выявления и анализа закономерностей распределения размеров деталей при их рассеянии применяются методы математической статистики.

КРИВЫЕ РАСПРЕДЕЛЕНИЯ И ОЦЕНКА ТОЧНОСТИ ОБРАБОКи. Математическая статистика была точной научной базой, на которой начали проводить первые исследования точности технологических процессов. Первым шагом в этом направлении было изучение и анализ кривых распределения. Построение кривых распределения производится следующим образом. Всю совокупность измерений (точность измерения должно быть не ниже 0.1 допуска (разброса значений) исследуемой величины) интересующей нас величины (например, какого-либо размера в партии заготовок, обработанных при определенных условиях) разбивают на ряд групп: в каждую группу входят величины, результаты измерения которых находятся в пределах установленного интервала. Интервалы, число которых обычно берут в пределах 7-11, откладывают по оси абсцисс, а количество размеров, присоединяющиеся на каждый интервал, по оси ординат.

После соединение нанесенных на график точек получают ломаную линию, называемую полигоном распределения. В место абсолютного количества m деталей в каждом интервале по оси ординат откладывают отношение этого количества к общему количеству n, деталей в партии; данное отношение называется относительной частотой или частостью.

На рисунке показан полигон распределения диаметральных размеров колец, подвергнутых предварительному обтачиванию; из него видно, что на средние интервалы размеров приходится большее количество колец. При увеличении количества деталей в партии, сужение интервалов и увеличения их числа ломанная линия приближается к плавной кривой. В качестве самой приближенной меры точности исследуемого процесса обработки может служить поле рассеяния размеров. Величину поля рассеяния можно брать по полигону распределения или по таблице измерения исследуемых значений. Чем уже поле рассеяния, тем точнее исследуемый технологический метод.

Числовые характеристики случайных величин. При решении практических вопросов определения случайных погрешностей, зачастую достаточно указать только числовые характеристики (параметры) распределения случайных величин. Они в сжатой форме выражают наиболее существенные особенности распределения, значительно облегчаются решение многих вероятностных задач.

Характеристики положения: математическое ожидание, мода, медиана. Эти характеристики указывают некоторое среднее ориентировочное значение около которого группируются все возможные значения случайные величины.

Моменты. Дисперсия и среднеквадратное отклонение. Центрированная случайная величина – отклонение случайной величины х от ее математического ожидания.

Математическое ожидание центрированной случайной величины равно нулю. Действительно

Очевидно, центрирование случайной величины равносильно переносу начала координат в среднюю точку, абсцисса которой равна математическому ожиданию.

Моменты центрированной случайной величины носят название центральных моментов.

Рассмотрим второй центральной момент.

Относительно произвольно выбранной абсциссы со значением а. Преобразуем это выражение.

при а = m_x – полученная величина достигает минимума. Таким образом второй центральный момент из всех вторых моментов является минимальным.

В виду особой важности ему присвоили специальное название – дисперсия (с английского - разброс) и обозначают следующим образом.

 

Для непосредственного вычисления дисперсии применяют формулы:

Дисперсия характеризует рассеяния случайной величины относительно математического ожидания. Она имеет размерность квадрата случайной величины. Для того, чтобы пользоваться дисперсией имеющей ту же размерность из нее извлекают квадратный корень

Которое называют среднеквадратичным отклонением. Для упрочнения записи среднеквадратичное отклонение и дисперсию обозначают через σ_х, Д_х.

Третий центральный момент. Служит для характеристики асимметрии распределения. Действительно в сумме

при суммарном относительно m_x законе распределения и нечетном S, каждому положительному значению слагаемого соответствует равное ему по абсолютной величине отрицательное слагаемое, поэтому вся сумма равна нулю, что то же самое справедливо и для интеграла

как интеграл в симметричных пределах от нечетной функции. При малейшем отклонении от симметрии, как сумма, так и интеграл будут иметь значения отличные от нуля.

Естественно, в качестве характеристики асимметрии принять один из нечетных моментов. Простейшие из них имеют размерность куба. Чтобы получить безразмерный коэффициент асимметрии значение μ₃ делят на куб среднеквадратичного отклонения.

f(x)

 

m₁ m₂ x

1 – положительная асимметрия S_k>0; 2 – отрицательная асимметрия S_k<0.

Четвертый центральный момент – определяет крутость или островершинность. Эти свойства описываются коэффициентом называемым эксцессом.

f(x)

Ех>0

Ех=0

Ех<0

 

 

m_x х

число 3 вычитается потому, Что для нормального распределения величина

 

Многочисленные исследования показали, что в технологии машиностроения распределение размеров чаще всего происходит по нормальному закону или закону Гаусса. Она является результатом действия большого числа различных факторов с одинаковой по интенсивности своего влияния, этому закону подчиняются многие непрерывные случайные величины: размеры деталей, обработанных на настроенных станках; вес заготовок и деталей машин; твердость и другие характеристики механических свойств материала; высота микронеровностей на обработанных поверхностях; погрешности измерений и другие величины.

Кривая Гаусса выражается следующим уравнением:

;

где s - среднее квадратическое отклонение аргумента;

е – основание натуральных логарифмов;

a – значение абсциссы, при которой ордината y кривой достигает max.

Величина, а является центром распределения (группирование) аргумента и в тоже время его средней арифметической.

Закон Гаусса двухпараметрический (параметр s и а).

Ординаты вершины кривой x=а

Точки перегиба кривой лежат на расстояниях s от ее оси симметрии. Их ординаты

-

Величина среднего квадратичного отклонения s, являющаяся мерой точности характеризует форму кривой распределения. При малых значениях s точность исследуемого метода повышается и кривая получается сильно вытянутой вверх с малым полем рассеяния. При больших значениях s кривая получается очень пологой и поле рассеяния растет.

Определение s по результатам измерений производится по следующей формуле

,

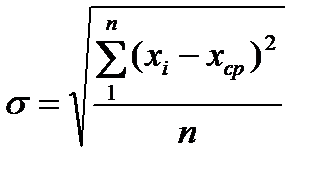где n-количество произведенных измерений (рекомендуется брать равным 50)

x_i- значение текущего измерения;

x_ср- среднее арифметическое из произведенных измерений;

,

Геометрически кривая нормального распределения простирается в обе стороны вдоль оси абсцисс беспредельно, асимптотически приближаясь к этой оси, как это видно из рис.

 

Для теоретических расчетов предельные отклонения (при использовании нормального закона рассеяния), выражаемое в долях среднеквадратического отклонения s(x), ограничивают обычно величинами x=±3s.

При этих значениях x; 99,73% отклонений случайной величины попадают в область внутри установленных пределов и 0,27% выходят из них.

Таким образом, вычислив по данным наблюдений значение s, можно охарактеризовать точность исследуемого метода произведением 6s. В этом случае мы имеем практически 100-процентную годность обрабатываемых деталей, т.к. вероятное количество брака менее 0,3%.

Кроме закона Гаусса встречаются другие законы распределения размеров обрабатываемых деталей в партии.

Если на выполняемый размер оказывает влияние систематическая равномерно возрастающая погрешность (погрешность, вызываемая размерным износом режущего инструмента) протекающая по закону прямой, то распределение происходит по закону равной вероятности.

Если на выполняемый размер влияет закономерно изменяющаяся погрешность, возрастающая сперва замедленно, а затем ускоренно, то распределение размеров проходит по закону треугольника (Симпсона). Это распределение может иметь место при совместном действии размерного износа режущего инструмента с сильно выраженной фазой начального износа и увеличения силы резания в конце стойкости инструмента в результате его прогрессирующего затупления.

Рассмотрим кривые распределения погрешностей взаимного положения и погрешностей формы поверхностей обработанных деталей. Эти погрешности являются положительными величинами, они изменяются от нуля до определенного значения. Кривая распределения эксцентриситетов R ступенчатых цилиндрических деталей имеет несимметричную форму.

Закон эксцентриситета (закон Релея) Характер изменения кривой говорит о том, что деталей с нулевым эксцентриситетом нет; большая часть деталей имеет средний по величине эксцентриситет; деталей с большим эксцентриситетом имеется мало.

Закону эксцентриситета (закону Релея) следует также распределение значений непараллельности и неперпендикулярности двух плоскостей; неперпендикулярность оси детали к ее торцовой поверхности; разностенность полых деталей (при нефиксированной плоскости измерения). Этот закон однопараметрический. Среднеарифметическое значение X_cp эксцентриситетов R связано со среднеквадратичным отклонением постоянным соотношением

Х_ср=1,92s.

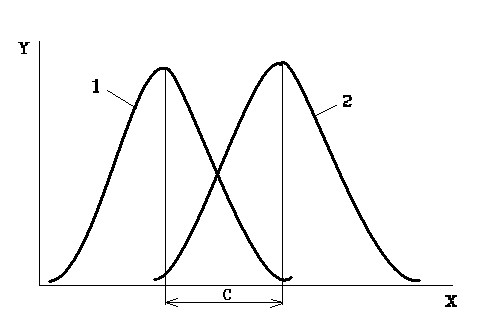
Систематическая постоянная погрешность не оказывает влияния на форму кривой распределения. Влияние этой погрешности сказывается лишь в том, что кривая распределения сдвигается вправо на величину с этой погрешности.

Если на ряду со случайными имеются и систематические закономерно изменяющиеся погрешности, то кривая распределения искажается. Так в качестве примера показана кривая, представляющая собой композицию кривой Гаусса и кривой равномерной вероятности. Эта кривая может получиться в том случае, когда на точность обработки оказывает сильное влияние размерный износ инструмента.

Кривая распределения для двух одинаковых партий деталей, обработка которых производится при двух различных настройках станка, получается двухвершинной. Для нескольких настроек может получиться многовершинная кривая.

При большом количестве настроек многовершинность сглаживается и кривая приобретает форму кривой нормального распределения, но с более широкой базой. Увеличение ширины базы происходит на величину погрешности настройки D_н.

Статический метод исследования на базе кривых распределения дает возможность объективно оценить точность различных способов механической обработки. Данный метод универсален. Его можно применить для исследования точности выполнения заготовок, сборочных операций, операций технического контроля, а также для целого ряда таких специфических операций, как балансировка, холодная правка и пр.. Он особенно удобен (а часто и незаменим) в тех случаях, когда механизм явления не изучен. Целесообразно применять его также для практической проверки результатов и выводов, полученных на основе расчетно-аналетического метода. К существенным недостаткам этого метода относится, то, что он не вскрывает сущность физических явлений и фактов, влияющих на точность обработки, а также то, что на его базе не выявляются конкретные возможности повышения точности. Метод фиксирует результаты законченного этапа, т.е. «обращен в прошлое». Полученные ранее значения s не могут быть использованы, если в условиях выполнения данной операции произошли изменения (режим резания, способ установки заготовки и т.п.). В этом случае необходимо определить новое значение s.

Точечные диаграммы и их применения для исследования точности. Другой метод исследования точности основан на построении точечных диаграмм. По горизонтальной оси откладывают номера обрабатываемых деталей или номера групп деталей в той последовательности, как они сходят со станка. По вертикальной оси в виде точек откладывают результаты измерений деталей или среднеарифметическое значение размеров деталей входящих в каждую группу

Сущность метода точечных диаграмм заключается в том, что в процессе изготовления данной продукции периодически берут пробы в количестве от двух до десяти деталей. Результаты измерений этих деталей, проводимых универсальными инструментами немедленно обрабатывают и наносят на специальную (контрольную) диаграмму.

На этой диаграмме предусмотрены параллельные прямые a и a, определяющие границы поля допуска, и прямые б и б, определяющие поле рассеяния средних групповых значений и называющиеся контрольными прямыми. Место контрольных прямых находят на основе теоретических положений статического контроля, рассматриваемых в специальных курсах и литературах.

Анализ диаграммы представленный на рисунке Вначале процесс обработки протекает нормально и ломаная линия не выходит за пределы контрольных прямых. При контроле группы A установлен выход ломаной линии за пределы контрольных границ. Это служит сигналом для поднастройки станка регулированием, или сменой инструмента, или проверки положения упоров.Применением статического контроля предупреждается брак, т.к. контролируется не вся совокупность уже изготовленных деталей (как при обычных способах контроля), а правильность выполнения самого технологического процесса при обнаружении отклонения своевременно применяют меры для их устранения. При статическом контроле значительно сокращается количество контролеров, т.к. выборочной проверке подвергаются только 5-10% продукции.

Управление точностью обработки по выходным данным. Управление по выходным данным. Компенсация погрешности об­работки таким методом (получил название метода активного контроля) осуществляется, как правило, периодически в момент, когда погрешность размера приближается к границе поля допуска. Преимущества заключа­ются в простоте определения поправки, которую необходимо внести для компенсации погрешности обработки, а недостаток - запаздывание в по­лучении информации, так как измеряют погрешность обработки после того как вся деталь или ее часть обработана. Активный контроль нашел сравнительно широкое распространение. Его функции сводятся, главным образом, к компенсации погрешности, обусловленной совокупным действием систематических факторов как постоянных по величине, так и изменяющихся во времени. К таким фак­торам в первую очередь относятся геометрические погрешности и изна­шивание.

В станкостроении наиболее распространен активный контроль н шлифовальных станках. При обработке на этих станках изнашивание шлифовального круга доминирует среди других погрешностей и отлича ется большой скоростью изменения. На рис. 1.10.17 приведена система активного контроля. В процессе обработки партии деталей каждая деталь после схода со станка подверга ется измерению скобой (рис. 1.10.17, а). Измеренная величина в виде электрического сигнала поступает на сравнивающее устройство, где она сопоставляется с заданным значением. Если между этими величинами имеется разница, то на этой основе формируется величина управляющего сигнала, поступающего на исполнительный механизм (подналадчик). вносящий поправку в относительное положение рабочих поверхностей, н данном случае - в относительное положение режущих кромок инстру­мента и технологических баз заготовки.

Еще одно преимущество методов управления этой группы заключа ется в измерении точности в статическом состоянии, когда деталь изме­ряется вне станка. Однако, как уже отмечалось, это преимущество влечем за собой и недостаток в виде увеличения запаздывания во внесении по правки, а это отражается отрицательно на повышении точности этим путем. При использовании систем активного контроля приходится решать такие задачи, как уменьшение величины запаздывания в управлении точ ностью и выделение систематической составляющей из суммарной по грешности.

А - контроль детали после обработки; б - контроль детали на станке

С целью сокращения запаздывания стали создавать системы актив­ного контроля, где измеритель /, контролирующий обработанную деталь, располагается следом за режущим инструментом (рис. 1.10.17, б). При гаком измерении существенно уменьшается величина запаздывания, но при этом появляются дополнительные трудности с измерением детали. Измерение осуществляется на станке в условиях съема стружки, подачи ('С)Ж, вибраций станка и т. п. Чтобы определить момент внесения поправки, применяют 100 %-ный или выборочный контроль и строят точечные диаграммы

Сложность управления по данным точечной диаграммы заключается н том, что действие случайных факторов затрудняет определение по­грешности, обусловленной систематическими факторами, и не позволяет точно прогнозировать погрешность следующей детали. Чтобы выявить влияние на погрешность обработки совокупного действия систематиче­ских факторов, строят точечную диаграмму групповых средних размеров.

Определение размера исходной заготовки и операционных размеров при расчете припусков.

Исходная заготовка отличается от детали тем, что на всех обрабатываемых поверхностях предусмотрены припуски – слои материала, подлежащие удалению с поверхности заготовки в процессе обработки для получения заданной точности и шероховатости. Материал, оставленный в выемках, пазах и отверстиях отливок и поковок образует напуск, также удаляемый при обработке. Напуском является также слой

материала проката, превышающий размеры заготовки с учётом припуска на обработку.

Припуски разделяют на общие – удаляемые в течение всего процесса обработки и межоперационные(промежуточные), удаляемые при выполнении отдельных операций. Межоперационный припуск определяется разностью размеров заготовки, полученных на смежных предшествующем и выполняемом переходах.

Общий припуск равен сумме межоперационных припусков по всем технологическим операциям.

Припуски могут быть симметричными (для тел вращения) и асимметричными – (призматические детали).

Различают номинальный, минимальный и максимальный припуск.

Минимальный припуск, т.е. наименьший слой металла, снимаемый при обработке, есть разность между

наименьшим размером заготовки и наименьшим размером после выполнения данного перехода. Максимальный

припуск равен номинальному припуску минус допуск на выполнение данного перехода.

Номинальный припуск – разность между номинальными размерами поверхности после предшествовавшего

и после данного перехода.

Максимальный припуск есть разность между наименьшим размером поверхности после выполнения пред-

шествовавшего перехода и наименьшим её размером после выполнения данного перехода.

Существуют нормативные данные, суммируя которые можно получить величину минимального припуска.

Имеются так же ГОСТ на значения общих припусков на обработку отливок и поковок. При оценке величины

общего припуска учитываются факторы:

1) размер и конструктивные формы;

2) материал и способ получения заготовки;

3) величина дефектного слоя;

4) погрешность установки;

5) степень деформации.

Важно, чтобы припуски на обработку были возможно меньшими в целях экономии металла, времени и т.д.

Для этого, чтобы ограничить значения промежуточных припусков, назначают технологические допуски на отдельные переходы.

Обычно технологические промежуточные допуски на охватываемую поверхность (шейка вала) назначают

в минус, а на охватывающую (отверстия) – в плюс. В любом случае промежуточный допуск направлен в тело

металла.

Минимальный припуск – минимальная необходимая толщина слоя материала для выполнения данной опе-

рации. Он является исходной величиной при расчёте припусков.

Припуски на обработку определяются двумя методами:

1) опытно-статистический – при котором значения общих и промежуточных припусков определяют по

справочным таблицам, составленным на основе обобщения производственного опыта. Недостаток метода – нет

учёта конкретных условий построения ТП. Полученные припуски, как правило, завышены, так как ориентиру-

ются на полное отсутствие брака;

2) расчётно-аналитический метод (профессор В.М. Кован), согласно которому промежуточный припуск

должен быть таким, чтобы при его снятии устранялись погрешности обработки и дефекты поверхностного

слоя, полученные на предшествующем переходе, а так же погрешности установки на данном переходе.

Основа метода – определение Z min.

Величину минимального промежуточного припуска определяют следующ

⇐ Предыдущая123456789

Поделиться:

Воспользуйтесь поиском по сайту: