 |
Усреднение. Моменты случайной величины
|
|
|
|
Например, простейший «первый» момент – «математическое ожидание»
Среднее значение сигнала при осреднении по ансамблю в момент t1 определяется по формуле
. (6-53)
При осреднении данной k- й реализации во времени среднее значение
. (6.54)
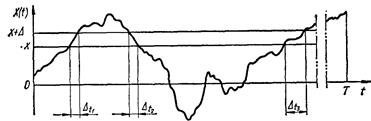
Рис. 6.16. К определению плотности распределения случайного сигнала
Среднее значение сигнала характеризует его постоянную составляющую. Среднее значение стационарного сигнала равно постоянной величине, а стационарного и эргодического сигнала, найденное путем временного осреднения одной реализации — среднему значению по ансамблю реализаций.
Среднее значение квадрата сигнала характеризует суммарную интенсивность данной реализации:
(6.55)
Среднее квадратическое значение сигнала равно корню квадратному из среднего значения квадрата:
Центральные моменты
Например, второй центральный момент –«дисперсия»
С. к. о. сигнала (для стационарных и эргодических процессов?)
.
Стационарный и эргодический случайный сигнал удобно характеризовать двумя составляющими: постоянной и переменной. Первая равна среднему значению сигнала 
, а вторая оценивается дисперсией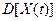 
, характеризующей рассеяние сигнала по отношению к среднему значению, и равна среднему значению квадрата отклонения сигнала от его среднего значения:
. (6.56)
Преобразуя уравнение (6.56), получим
.
Следовательно, дисперсия стационарного и эргодического сигнала равна разности между средним значением квадрата и квадратом среднего значения и характеризуется постоянным числом.
С. к. о. сигнала
.
Функция распределения, или интегральный закон распределения, Р(X<x1) равна вероятности того, что сигнал X(t) не превосходит заданного значения:
|
|
|
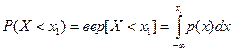. (6.58)
Вероятность того, что 
, очевидно, равна нулю, а вероятность того, что 
, равна 1. Следовательно, функция распределения Р(X) изменяется от 0 до 1.
Рис. Функция распределения
Вероятность нахождения сигнала в интервале между значениями x1 и х2
Плотность распределения случайного сигнала, или дифференциальный закон распределения р(х) характеризует вероятность того, что мгновенные значения сигнала в произвольный момент времени будут находиться в заданном интервале значений. Рассматривая реализацию случайного сигнала X(t) (рис. 6.16), вероятность нахождения сигнала в интервале значений х и х + ∆ можно определить, вычисляя отношение
где 
—суммарное время нахождения сигнала X(t) в интервале между значениями х и х + ∆ в течение времени Т, Т — продолжительность реализации X(t);
Одномерная плотность распределения сигнала
.
ПРВ есть производная от функции распределения.
=>
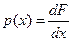, т.е. p(x) есть вероятость попадания случайной величины в полуинтервал (х, x+dx].
Свойства:
p(x)>0
Одномерная плотность распределения р(х) не содержит координаты времени и не отражает статистической зависимости значений сигнала при изменении времени. Плотность распределения сигнала — действительная неотрицательная функция и для стационарного эргодического сигнала может быть определена по одной реализации. Через плотность распределения удобно выражается среднее значение случайного сигнала
и среднее значение его квадрата
Функция распределения, или интегральный закон распределения, для стационарного и эргодического сигнала также может быть определена по одной его достаточно протяженной во времени реализации.
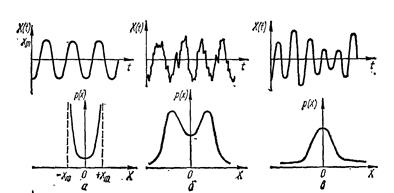
Рис. 6.17. Примеры сигналов и графики плотностей распределения:
а — гармонического, б — суммы гармонического и случайного, в — узкополосного случайного шума, г — широкополосного случайного шума.
|
|
|
Плотность распределения и функция распределения являются весьма важными характеристиками случайного сигнала и измеряются статистическими анализаторами. По известной плотности распределения можно определить другие важные параметры случайного сигнала — функцию распределения, вероятность нахождения сигнала в заданном интервале и др. Кроме этого, характер плотности распределения дает возможность установить структуру сигнала, например наличие в нем гармонической составляющей. Покажем это на примере сравнения реализаций и плотностей распределения четырех сигналов: гармонического (рис. 6.17, и), суммы гармонического и случайного (рис. 6.17, б), узкополосного (рис. 6.17, в) и широкополосного (рис. 6.17, г) случайных шумов. Гармонический сигнал в данном случае рассматривается как случайный, поскольку предполагается, что фаза его является случайной величиной. Плотность распределения гармонического сигнала (рис. 6.17, а, б) со случайной фазой представляется чашеобразной симметричной кривой, а случайных сигналов (рис. 6.17, в) и (рис. 6.17, г) чаще всего подчиняется закону Гаусса (п. 4.2) и имеет куполообразную симметричную форму. Сумма гармонического и случайного сигналов имеет характерные особенности плотностей распределения их обоих — как гармонического, так и случайного сигналов — это иногда дает возможность по виду плотности распределения определить состав данного исследуемого сигнала.
Функциональный анализ
При решении задач обработки сигналов возникают следующие вопросы:
-как оценить сходство сигналов,
-как оценить состав сложного сигнала,
Векторное представление сигналов бесконечномерном пространстве
Математический раздел «Функциональный анализ» использует модель сигнала как вектора в специальном бесконечномерном пространстве. Приведенные далее системы аксиом не являются исчерпывающе полными, но достаточными для понимания следующих разделов. В некоторых случаях вывод показан на основе качественных представлений.
|
|
|
