Вычислим АКФ прямоугольного импульса

- при 0<τ< Т

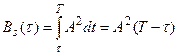
- при -T<τ<0

- при |τ| > Т

Объединяя результаты, можно записать

 

Рис. График корреляционной функции прямоугольного импульса

 

С учетом четности, графическое представление АКФ обычно производится только для положительных значений t. Знак +t в выражении (8.1.1) означает, что при увеличении значений t от нуля копия сигнала s(t+t) сдвигается влево по оси t. На практике сигналы обычно задаются на интервале положительных значений аргументов от 0 до Т, что дает возможность продления интервала нулевыми значениями, если это необходимо для математических операций. В этих границах вычислений более удобным для построения вычислительных алгоритмов является сдвиг копии сигнала вправо по оси аргументов, т.е. применение в выражении (8.1.1) функции копии s(t-t):

B_s(t) = s(t) s(t-t) dt.

АКФ неограниченных во времени сигналов. Для сигналов, заданных на определенном интервале [a, b], вычисление АКФ производится с нормировкой на длину интервала [a, b]:

B_s(t) = s(t) s(t+t) dt. (8.1.1'')

В пределе, для сигналов с бесконечной энергией, АКФ может быть получена как среднее значение скалярного произведения сигнала и его копии при устремлении интервала длительности сигнала Т к бесконечности:

B_s(t) = .

АКФ по данному выражению имеет физическую размерность мощности, и равна средней взаимной мощности сигнала и его копии в функциональной зависимости от сдвига копии.

АКФ периодических сигналов. Энергия периодических сигналов бесконечна, поэтому АКФ периодических сигналов вычисляется по одному периоду Т, с усреднением скалярного произведения сигнала и его сдвинутой копии в пределах этого периода:

B_s(t) = (1/Т) s(t) s(t-t) dt. (8.1.2')

Свойства КФ периодических сигналов

1. При t=0 значение нормированной на период АКФ в этом случае равно не энергии, а средней мощности сигналов в пределах периода:

2. Свойство четности сохраняется:

.

3. Значение КФ при τ = 0 по-прежнему является максимально возможным:

4. АКФ периодического сигнала является периодической функцией с тем же периодом, что и сам сигнал:

.

5. Если сигнал не содержит дельта-функций, его КФ будет непрерывной функцией.

6. Отметим, что полученный результат не зависит от начальной фазы гармонического сигнала, что характерно для любых периодических сигналов и является одним из свойств КФ.

7. Размерность КФ периодического сигнала — квадрат размерности сигнала (В², если сигнал — напряжение).

Вычислим АКФ прямоугольного радиоимпульса

Так, для сигнала s(t) = A cos(w₀t+j₀) при T=2p/w₀ имеем:

B_s(t) = A cos(w₀t+j₀) A cos(w₀(t-t)+j₀) = (A²/2) cos(w₀t).

АКФ случайных функций

АКФ дискретных сигналов. При интервале дискретизации данных Dt = const вычисление АКФ выполняется по интервалам Dt = Dt и обычно записывается, как дискретная функция номеров n сдвига отсчетов nDt:

B_s(n) = Dt s_k×s_k-n. (8.1.3)

Дискретные сигналы обычно задаются в виде числовых массивов определенной длины с нумерацией отсчетов к = 0,1,…N, а вычисление дискретной АКФ выполняется в одностороннем варианте с учетом длины массивов по формуле:

B_s(n) = 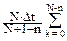s_k×s_k-n. (8.1.3')

Множитель N/(N+1-n) в данной функции является поправочным коэффициентом на постепенное уменьшение числа перемножаемых и суммируемых значений (от N до N-n) по мере увеличения сдвига n. Без этой поправки для нецентрированных сигналов в значениях АКФ появляется тренд суммирования средних значений.

Практически, дискретная АКФ имеет такие же свойства, как и непрерывная АКФ. Она также является четной, а ее значение при n = 0 равно энергии дискретного сигнала.

Кодовые сигналы являются разновидностью дискретных сигналов. На определенном интервале кодового слова М×t они могут иметь только два амплитудных значения: 0 и 1 или 1 и –1. При выделении кодов на существенном уровне шумов форма АКФ кодового слова имеет особое значение. С этой позиции наилучшими считаются такие коды, значения боковых лепестков АКФ которых минимальны по всей длине интервала кодового слова при максимальном значении центрального пика. К числу таких кодов относится код Баркера, приведенный в таблице 8.1. Как видно из таблицы, амплитуда центрального пика кода численно равна значению М, при этом амплитуда боковых осцилляций при n ¹ 0 не превышает 1.

Таблица 8.1.

M	Сигнал Баркера	АКФ сигнала
	1, -1	2, -1
	1, 1, -1	3, 0, -1
	1, 1, 1, -1	4, 1, 0, -1
	1, 1, -1, 1	4, -1, 0, 1
	1, 1, 1, -1, 1	5, 0, 1, 0, 1
	1, 1, 1, -1, -1, 1, -1	7, 0, -1, 0, -1, 0, -1
	1,1,1,-1,-1,-1,1,-1,-1,1,-1	11,0,-1,0,-1,0,-1,0,-1,0,-1
	1,1,1,1,1,-1,-1,1,1-1,1,-1,1	13,0,1,0,1,0,1,0,1,0,1,0,1

Функции автоковариации (ФАК). В практике обработки и статистического анализа дискретных данных и функций вместо корреляционных функций обычно используются ковариационные функции, хотя эти два термина очень часто используются как синонимы. Строго корректно, под функциями автоковариации (ФАК) следует понимать вторые центральные моменты распределения числовых величин в цифровых массивах:

C_s(n) = (s_k- )×(s_k-n- ), (8.1.4)

где - среднее значение функций. Максимум ФАК, как и АКФ, соответствует n = 0 и равен дисперсии сигнала s_k. Из сравнения (8.1.4) с выражением (8.1.3) отсюда следует, что дисперсия сигналов (квадрат стандартного отклонения от среднего значения) равна средней энергии сигнала по интервалу его задания. Соответственно, связь ФАК с энергетическим спектром (плотностью распределения мощности сигнала) через преобразование Фурье сохраняется аналогичной АКФ.

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: