 |
Скалярное произведение сигналов
|
|
|
|
Угол между векторами(норма и метрика уже определена) можно определить через понятие скалярного произведения элементов линейного пространства. Если в обычном трехмерном пространстве известны два вектора 
и 
, то квадрат модуля их суммы равен
,
где
- скалярное произведение сигналов, зависящее от угла между ними.
Рисунок
Действуя по аналогии, вычислим энергию суммы двух сигналов u и v:
. (a)
В отличии от самих сигналов их энергии не аддитивны – энергия суммарного сигнала содержит в себе так называемую взаимную энергию
. (b)
Сравнивая между собой формулы (a) и (b), примем, что скалярное произведение вещественных сигналов u и v равно
,
а также косинус между ними:
.
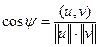В соответствии с формулой угол должен лежать в интервале от 0° до 180°.
Скалярное произведение обладает следующими свойствами:
1) 
;
2) 
;
3) 
, где λ – вещественное число;
4) 
.
Справедливо фундаментальное неравенство Коши-Буняковского
.
Линейное пространство с таким скалярным произведением, называется вещественным гильбертовым пространством.
Если сигналы принимают комплексные значения, то можно определить комплексное гильбертово пространство, введя в нем скалярное произведение по формуле
,
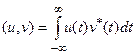такое что 
.
Корреляционный анализ
Корреляция (correlation), и ее частный случай для центрированных сигналов – ковариация, является методом анализа сигналов, его смысл состоит в количественном измерении степени сходства различных сигналов.
Автокорреляционная функция (autocorrelation) показывает степень сходства между сигналом и его сдвинутой копией ( скользящей по аргументу ) — чем больше значение корреляционной функции, тем это сходство сильнее. Автокорреляция позволяет оценить среднестатистическую зависимость текущих отсчетов сигнала от своих предыдущих и последующих значений (так называемый радиус корреляции значений сигнала), а также выявить в сигнале наличие периодически повторяющихся элементов.
|
|
|
Взаимная корреляция сигналов характеризует определенную корреляцию явлений и физических процессов, отображаемых данными сигналами, и может служить мерой “устойчивости” данной взаимосвязи при раздельной обработке сигналов в различных устройствах.
Приведем один из вариантов использования метода. Допустим, что имеется сигнал s(t), в котором может быть (а может и не быть) некоторая последовательность x(t) конечной длины Т, временное положение которой нас интересует. Для поиска этой последовательности в скользящем по сигналу s(t) временном окне длиной Т вычисляются скалярные произведения сигналов s(t) и x(t). Тем самым мы "прикладываем" искомый сигнал x(t) к сигналу s(t), скользя по его аргументу, и по величине скалярного произведения оцениваем степень сходства сигналов в точках сравнения. В функциональном пространстве сигналов эта степень сходства может выражаться в нормированных единицах коэффициента корреляции, т.е. в косинусе угла между векторами сигналов, и, соответственно, будет принимать значения от 1 (полное совпадение сигналов) до -1 (полная противоположность).
Особое значение методы корреляции имеют при анализе случайных процессов для выявления неслучайных составляющих и неслучайных параметров этих процессов.
Заметим, что в терминах "корреляция" и "ковариация" в настоящее время существует изрядная путаница. В иностранной литературе термин "ковариация" применяется к центрированным функциям, а "корреляция" – к произвольным. В отечественной литературе, и особенно в литературе по сигналам и их обработке, довольно часто применяется прямо противоположная терминология.
|
|
|
Принципиального значения это не имеет, но при знакомстве с литературными источниками стоит обращать внимание на принятое назначение данных терминов. При разработке настоящих лекций было принято решение использовать общепринятую международную терминологию, как согласованную по понятиям с основными положениями теории вероятностей и математической статистики.
|
|
|
