 |
Линейное пространство сигналов
|
|
|
|
Пусть М={s1(t), s2(t),…}- множество сигналов. Множество сигналов М образует вещественное линейное пространство, если справедливы следующие аксиомы:
1) Любой сигнал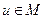 
при любых t принимает лишь вещественные значения.
2) Для любых 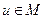и 
существует их сумма 
, причем w также содержится в М. Операция суммирования коммутативна: 
и ассоциативна: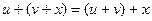 
.
3) Для любого сигнала 
и любого вещественного числа α определен сигнал 
.
4) Множество М содержит особый нулевой элемент 
, такой, что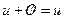 
для всех .
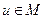Если математические модели сигналов принимают комплексные значения, то, допуская в аксиоме 3 умножение на комплексное число, приходим к понятию комплексного линейного пространства.
Элементы линейных пространств часто называют векторами, подчеркивая аналогию свойств этих объектов и обычных трехмерных векторов.
Понятие координатного базиса
Как и в обычном трехмерном пространстве, в линейном пространстве сигналов можно выделить специальной подмножество играющее роль координатных осей.
Говорят, что совокупность векторов 
, принадлежащих М является линейно независимой, если равенство
возможно лишь в случае одновременного обращения в нуль всех числовых коэффициентов 
.
Система линейно независимых векторов образует координатный базис в линейном пространстве. Какой либо элемент координатного базиса не может быть выражен в виде линейной комбинации оставшихся элементов. Если дано разложение некоторого сигнала s(t) в виде
то числа 
являются проекциями сигнала s(t) относительно выбранного базиса или коэффициентами разложения по базису.
Какой либо элемент координатного базиса не может быть выражен в виде линейной комбинации оставшихся элементов.
|
|
|
Нормированное линейное пространство. Энергия сигнала
Определение понятия длина вектора позволяет вычислять насколько один сигнал больше другого. Длину вектора называют нормой.
Линейное пространство сигналов L является нормированным, если каждому вектору 
однозначно сопоставлено число 
- норма этого вектора, причем выполняется следующие аксиомы нормированного пространства:
1) Норма неотрицательна, 
. Норма 
тогда и только тогда, если 
2) Для любого числа α справедливо равенство 
.
3) Если s(t) и p(t) – два вектора из L, то выполняется неравенство треугольника: 
.
Принято определять норму вещественных непрерывных сигналов следующим образом
Если сигнал дискретен то
Для комплексных сигналов норма
где * - символ комплексно-сопряженной величины.
Квадрат нормы фактически является энергией сигнала, именно такая энергия выделяется на резисторе с сопротивлением 1Ом, если к нему приложено напряжение s(t).
Энергетическая норма оказывается нечувствительной к изменениям формы сигнала, даже значительным, но происходящим на коротких отрезках времени.
Рисунок
Метрическое пространство
Линейное пространство становится метрическим пространством, если каждой паре элементов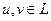 
сопоставлено неотрицательное число 
, называемое метрикой или расстоянием между этими элементами.
Обычно метрику определяют как норму разности двух сигналов:
.
Норму можно понимать как расстояние между данным элементом пространства и нулевым элементом: 
.
Метрика, независимо от способа ее определения, должна подчиняться аксиомам метрического пространства:
1) 
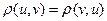- рефлексивность метрики.
2) 
3) Каков бы ни был элемент 
, всегда 
.
Зная метрику, можно судить, насколько один сигнал подобен по форме другому.
|
|
|
