 |
Операционный метод. Преобразования Лапласа
|
|
|
|
Решение дифференциальных уравнений операторным методом. Преобразование Лапласа является исключительно гибким и мощным методом, позволяющим путем стандартных процедур находить решения линейных дифференциальных уравнений с постоянными коэффициентами. Именно это свойство обусловило его широкое использование в научных исследованиях и инженерных расчетах.
Пусть дифференциальное уравнение
(8-71)
устанавливает закон соответствия между сигналами на входе и выходе некоторой линейной стационарной системы.
Наложим некоторые ограничения. Сделаем допущение, что входной сигнал 
при t<0. Кроме того, исходя из специфики работы радиотехнических устройств, начальные условия выберем нулевыми: 
. Наконец, примем, что область допустимых входных сигналов не содержит в себе функций, столь быстро нарастающих во времени, что для них не существует преобразования Лапласа.
Метод операционного исчисления основан на том, что над оператором дифференцирования 
и некоторой функцией (изображением) X(s) от этого оператора, призводяться такие действия, что дифференцированию функции x(t) соответствует умножению оператора s на функцию X(s):
а интегрированию- деление функции X(s) на оператор s:
.
Обозначим закон соответствия между оригиналами и изображениями следующим образом:
,
Вычислив преобразования Лапласа от обеих частей дифференциального уравнения () уравнения, получим
(8.72)
Важнейшей характеристикой, на которой основан операторный метод, является отношение изображений выходного и входного сигналов:
называемое передаточной функцией или операторным коэффициентом передачи рассматриваемой системы.
В соответствии с формулой (8.72)
|
|
|
(8.74)
Если эта функция известна, то поиск выходной реакции системы на заданное входное воздействие разбивается на три этапа:
l. 
,
2. 
,
|3. 
.
Термин «операторный метод» исторически восходит к известным работам Хевисайда, который еще в конце прошлого века предложил символический способ решения дифференциальных уравнений, описывающих переходные процессы в линейных электрических цепях. Метод Хевисайда основан на символической замене оператора дифференцирования d/dt комплексным числом s.
Свойства передаточной функции. Сравнивая формулы (8.74) и (8.41), можно убедиться, что функция К(s) есть результат аналитического продолжения частотного коэффициента передачи К(jω) с мнимой оси jω на всю плоскость комплексных частот 
.
Функция К(s) аналитична на всей плоскости s, за исключением конечного числа точек p1, p2…pn, являющихся корнями знаменателя в формуле (8.74). Данные точки, т.е. корни уравнения
называют полюсами передаточной функции К(р).
Точки z1, z2,...,zm, представляющие собой корни уравнения
,
называют нулями данной передаточной функции.
Вынося общий множитель К0, возникающий при делении в (8.74) числителя на знаменатель, получаем так называемое нуль-полюсное представление передаточной функции:
(8.75)
Вещественность коэффициентов дифференциального уравнения (8.72) обусловливает следующее свойство нулей и полюсов: все эти числа либо вещественны, либо образуют комплексно-сопряженные пары.
Часто используют наглядный прием отображения передаточной функции с помощью карты нулей и полюсов, на которой некоторыми условными значками нанесены указанные точки. Саму функцию К(р), принимающую комплексные значения, нельзя непосредственно представить графически. Поэтому поступают так: над плоскостью с декартовой системой координат изображают трехмерную поверхность функции |К(s)| (рис. 8.4).
Поверхность имеет характерный вид «горного ландшафта»; бесконечно высокие вершины соответствуют полюсам, а впадины — нулям передаточной функции. Выполнив сечение этой поверхности с помощью плоскости, содержащей как вертикальную ось, так и ось jω, получим профиль АЧХ системы.
|
|
|
Рис. 8.4. Характер поверхности |К(s)| для передаточной функции, имеющей два комплексно-сопряженных полюса 
и один нуль z = 0
Полюсы передаточной функции линейной системы являются корнями характеристического уравнения (8.36). Поэтому для устойчивости системы необходимо и достаточно, чтобы эти полюсы располагались строго в левой полуплоскости комплексной переменной s. Нули передаточной функции в общем случае могут располагаться как в левой, так и в правой полуплоскостях.
Формула обращения. Заключительным этапом решения задачи о прохождении сигнала через линейную стационарную систему с помощью операторного метода является поиск оригинала, которому отвечает изображение ивъа(р) = = K(p)Um(p).
Рассмотрим частный случай, когда функция t/Bb[X(p) представляет собой отношение двух многочленов по степеням комплексной частоты:
Umui(p) = M(p)/N{p),
причем будем считать, что степень числителя m не превосходит степени знаменателя п и, кроме того, корни знаменателя ph i = 1, 2,..'.,и — простые.
Способ нахождения оригинала, отвечающего такому изображению, основывается на представлении функции и*ы*(р) в виде суммы элементарных дробей:
Коэффициенты С,- являются вычетами функции 1/вых(р) в точках полюсов, поэтому [14]
Как известно, изображению 1/(р — pi) соответствует оригинал exp(p;t). Таким образом, приходим к известной Ф'нгл формуле обращения:
(8.76)
Примеры нахождения выходных сигналов операторным методом. При практическом использовании операторного метода большую часть формальных вычислений можно исключить, обращаясь к широко распространенным таблицам преобразований Лапласа.
Пример. Найти переходную характеристику RC-цепи.
Здесь o(t)«->l/p, К(р) = 1Д1 +рт), поэтому 1/ВЬ1Х(р) = ]/[р(1+рт)]. Разлагая эту функцию на элементарные дроби, имеем
Оригиналы, соответствующие обоим слагаемым в правой части последней формулы, хорошо известны (см. [5, 6, 36]). Искомый
Передаточная функция 
равна отношению преобразования Лапласа 
реакции усилителя 
к изображению 
воздействия 
, вызвавшего эту реакцию, при нулевых начальных условиях. Пусть
|
|
|
; 
- изображения Лапласа для входного и выходного сигнала при нулевых начальных условиях. Передаточная функция усилителя
является функцией комплексного аргумента 
. Вид многочленов 
и 
и коэффициенты их зависят только от схемы цепи (усилителя) и параметров ее элементов.
Формально передаточная функция может быть получена из дифференциального уравнения
или
где 
, после замены оператора дифференцирования p на оператор Лапласа s и деления полученного уравнения на 
.
В связи с тем что изображение δ-функции
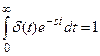
изображение при нулевых начальных условиях уравнения
будет
,
где
.
Применив формулу обращения, получим
;
здесь c – абсцисса абсолютной сходимости интеграла.
Таким образом, оригиналом передаточной функции является импульсная характеристика усилителя.
Когда требуется определить частотные характеристики, то переходят от преобразования Лапласа к преобразованию Фурье, положив 
,
где амплитудно-частотная характеристика
.
Пусть, например, передаточная функция имеет вид
.
следовательно, найдем АЧХ
.
Анализ последнего выражения показывает, что даже при всех положительных коэффициентах 
АЧХ 
может обратиться в бесконечность, если оба выражения, стоящие в круглых скобках знаменателя, обратятся в нуль. Это означает несходимость интеграла
,
обусловленную не затухающей с течением времени реакцией устройства на δ-функцию.
В таких случаях говорят, что работа устройства неустойчива и в нем возникли колебания выходного напряжения (тока). Так как колебания существуют без внешнего воздействия, то их называют автоколебаниями.
Если мнимые корни находятся в правой полуплоскости , то неустойчивость сохраняется, а при нахождении в левой полуплоскости – происходит затухание колебаний. Необходимые и достаточные условия отрицательности всех вещественных частей корней уравнения n-й степени с постоянными вещественными коэффициентами были даны Гурвицем (критерий устойчивости Гурвица, а также Михайлова и др.).
|
|
|
|
|
|
