 |
Частотный коэффициент передачи
|
|
|
|
При математическом исследовании систем особый интерес представляют такие входные сигналы, которые, будучи преобразованы системой, остаются неизменными по форме. Если имеется равенство
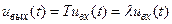, (8.19)
то uBX(t) является собственной функцией системного оператора Т, а число λ, в общем случае комплексное,— его собственным значением.
Комплексный сигнал 
при любом значении частоты ω есть собственная функция линейного стационарного оператора. Для этого воспользуемся интегралом Дюамеля вида (9) и вычислим
(20)
Отсюда видно, что собственным значением системного оператора является комплексное число
(21)
называемое частотным коэффициентом передачи системы.
Формула (21) устанавливает принципиально важный факт — частотный коэффициент передачи и импульсная характеристика линейной стационарной системы связаны между собой преобразованием Фурье.
Поэтому всегда, зная функцию K(jw), можно определить импульсную характеристику
(22)
Мы подошли к важнейшему положению теории линейных стационарных систем — любую такую систему можно рассматривать либо во временной области с помощью ее импульсной или переходной характеристик, либо в частотной области, задавая частотный коэффициент передачи. Оба подхода равноценны и выбор одного из них диктуется удобствами получения исходных данных о системе и простотой вычислений.
Частотный коэффициент передачи. Если на вход линейной динамической системы поступает сигнал, имеющий комплексную математическую модель вида
,
то сигнал на выходе
.
Подставляя эти выражения в (*), после сокращения на общий множитель находим частотный коэффициент передачи системы:
Итак, частотный коэффициент передачи любой динамической системы, описываемой обыкновенными дифференциальными уравнениями с постоянными коэффициентами, представляет собой дробно-рациональную функцию переменной jω; коэффициенты этой функции совпадают с коэффициентами дифференциального уравнения.
|
|
|
В инженерных расчетах частотный коэффициент передачи линейных систем часто находят методами теории цепей на основании принципиальных схем, не прибегая к составлению дифференциальных уравнений. Рассмотрим некоторые примеры.
Амплитудно-частотная и фазочастотная характеристики. Функция 
имеет простую интерпретацию: если на вход системы поступает гармонический сигнал с известной частотой ω и комплексной амплитудой 
, то комплексная амплитуда выходного сигнала
(24)
Часто пользуются представлением частотного коэффициента передачи в показательной форме:
(25)
Обе входящие сюда вещественные функции носят специальные названия: 
— амплитудно-частотная характеристика (АЧХ), 
— фазочастотная характеристика (ФЧХ) системы.
Рассмотрим двумерную ЛИС-системы с частотный коэффициент передачи системы (частотная характеристика или частотный отклик системы) 
и входным сигналом, представляющим собой комплексную синусоиду вида
где w1 и w2 — вещественные числа, называемые горизонтальной и вертикальной пространственными частотами соответственно. Выходной сигнал представляет собой комплексную синусоиду с теми же частотами, что и у входного сигнала, но с измененными амплитудой и фазой за счет комплексного множителя .
Можно показать, что частотный отклик периодичен с периодом 2π по обеим (горизонтальной и вертикальной) частотным переменным
В предыдущем разделе было показано, что для получения отклика двумерной ЛИС-системы на входной сигнал необходимо выполнить операцию свертки входного сигнала с импульсным откликом системы. Если представить входной сигнал в виде суперпозиции сдвинутых импульсов, то и выходной сигнал можно представить как суперпозицию сдвинутых импульсных откликов. Представление ЛИС-систем в частотной области также использует принцип суперпозиции, однако в этом случае элементарные последовательности являются комплексными синусоидами.
|
|
|
Ограничения, накладываемые на частотный коэффициент передачи. Далеко не каждая функция может являться частотным коэффициентом передачи физически реализуемой системы. Простейшее ограничение связано с тем, что импульсная характеристика h (t) такой системы обязана быть вещественной. В силу свойств преобразования Фурье (см. гл. 2) это означает, что
(26)
В соответствии с формулой (26) модуль частотного коэффициента передачи (АЧХ) есть четная, а фазовый угол (ФЧХ) — нечетная функция частоты.
Гораздо сложнее ответить на вопрос о том, каким должен быть частотный коэффициент передачи для того, чтобы выполнялись условия физической реализуемости (8.12) и (8.14). Приведем без доказательства окончательный результат, известный под названием критерия Пэли — Винера: частотный коэффициент передачи физически реализуемой системы должен быть таким, чтобы существовал интеграл
.
|
|
|
