 |
Сосредоточенные и распределенные физические системы.
|
|
|
|
Одним из критериев классификации физических радиотехнических систем является сопоставление физических размеров системы и рабочей длины волны.
Если характерный размер системы (например, наибольшая длина соединительных проводников цепи) оказывается гораздо меньше длины волны, то получается сосредоточенная система. Такая система может быть описана обычным дифференциальным уравнением. Анализ и расчет сосредоточенных радиотехнических систем проводят с помощью известных законов Кирхгофа.
В сосредоточенной электрической цепи всегда можно выделить физические области с преимущественной локализацией энергии электрического поля (конденсаторы) и магнитного поля (индуктивные элементы). Свойства сосредоточенных цепей слабо зависят от конфигурации соединительных проводников, поэтому для описания таких цепей принято использовать их абстрактные модели, называемые принципиальными схемами.
Например: RC- интегратор или LC колебательный контур.
На частотах в несколько Гигагерц (длина волны порядка 10 см), в так называемом сверхвысокочастотном (СВЧ) диапазоне, физические размеры большинства устройств оказываются сравнимыми с длиной волны передаваемых колебаний, так что становится необходимым учет конечного времени распространения сигнала. Обычные электрические цепи в столь высокочастотном диапазоне уже не могут использоваться и на смену им приходят системы с распределенными параметрами (распределенные или волновые системы). Такие системы могут быть описаны дифференциальным уравнением в частных производных.
Так, вместо соединительных проводников применяются отрезки металлических труб — волноводы, вместо колебательных LC-контуров — их распределенные аналоги, называемые объемными резонаторами. Теория, методы анализа и проектирования распределенных систем достаточно сложны и составляют содержание отдельных радиотехнических дисциплин.
|
|
|
Например: RC- интегратор или LC колебательный контур.
Линейные и нелинейные системы. Важнейший принцип классификации систем основан на том, что различные системы по-разному ведут себя при подаче на вход суммы нескольких сигналов. Если оператор системы таков, что справедливы равенства
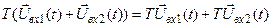, - свойство аддитивности
, - свойство однородности
где α — произвольное число, то данная система называется линейной. Условия выражают фундаментальный принцип суперпозиции.
Суперпозиция (принцип наложения или принцип независимости действия) – отклик линейной системы на взвешенную сумму входных сигналов равен взвешенной сумме откликов на отдельные входные сигналы, т.е. входной сложный сигнал раскладывается на составляющие и отдельно определяется выходной сигнал для каждой составляющей и суммируются. (В линейной системе действие суммы причин равно сумме действий, вызываемых каждой отдельно взятой причиной).
Систему называют линейной в том и только том случае, когда она удовлетворяет двум условиям: 1) если ее входной сигнал является суммой двух последовательностей, то выходной сигнал является суммой двух соответствующих выходных последовательностей; 2) пропорциональное изменение входного сигнала приводит к пропорциональному изменению выходного сигнала. Таким образом, если преобразование L[•] описывает действие линейной системы и 
; 
, то 
для всех входных сигналов х1 и х2 и любых комплексных констант а и b.
- линейная система, 
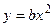-нелинейная система.
Линейная система (инерциальная и неинерциальная) описывается линейным дифференциальным уравнением, т.е. коэффициенты которого не зависят от сигнала.
|
|
|
Например, рассмотрим одиночный колебательный контур, находящийся в свободном режиме. Такой цепи соответствует однородное дифференциальное уравнение второго порядка.
Нелинейная система описывается дифференциальным уравнением, хотя бы один коэффициент которого зависит от сигнала, условия (4) не выполняются.
Например: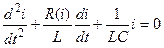 
.
Стационарные и нестационарные системы. Принято говорить, что система стационарна (инвариантна к сдвигу), если ее выходная реакция не зависит от того, в какой момент времени поступает входной сигнал или точнее сдвиг входной последовательности приводит к соответствующему сдвигу выходной последовательности.
Если Т — оператор стационарной системы, то из равенства
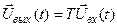(2)
следует, что
(3)
при любом значении t0.
Например, для двумерной стационарной системы выполняются следующие выражения
для всех последовательностей х и для всех целочисленных сдвигов (m1, m2).
Стационарные системы называют также системами с постоянными во времени параметрами. Если же свойства системы не инвариантны относительно выбора начала отсчета времени, то такую систему называют нестационарной (системой с переменными во времени параметрами или параметрической системой).
Линейно-параметрическая система описывается линейным дифференциальным уравнением с переменными коэффициентами (параметрическим дифференциальным уравнением). Хотя бы один коэффициент, которого является функцией времени или координаты, но не входного сигнала. Выполняется принцип суперпозиции.
Например: 
.
В этом уравнении коэффициент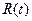 
является функцией времени (аргумента t).
Нелинейно-параметрическая система описывается дифференциальным уравнением, коэффициенты которого являются функцией входного сигнала и зависят от времени. Не выполняется принцип суперпозиции.
Например: 
.
Строго говоря, все физические системы, с которыми имеет дело радиотехника, в той или иной степени нелинейны и нестационарны. Однако существует много систем, которые весьма точно описываются линейными моделями. Так, практически всегда можно пренебречь нелинейностью обычных резисторов, конденсаторов и некоторых индуктивных элементов.
Нелинейные радиотехнические устройства содержат в себе обычно такие элементы, как полупроводниковые диоды и транзисторы, имеющие вольт-амперные характеристики сложного вида, а также квантователи в составе АЦП.
|
|
|
Теория нелинейных систем оказывается, как правило, довольно сложной. Далеко не все результаты могут быть получены здесь аналитическим путем. Однако именно с помощью нелинейных элементов осуществляются важнейшие преобразования радиотехнических сигналов.
Важным признаком классификации систем является возможность возникновения в результате преобразования сигнала колебаний новых частот, т.е. преобразование спектра сигнала. Т.к. гармонические функции являются собственными функциями операторов интегрирования и дифференцирования, то в линейных стационарных системах появления составляющих сигнала с новыми частотами не происходит. В нелинейных и параметрических системах происходит преобразование спектра с появлением новых частот.
Линейные стационарные системы (ЛС-системы) или линейные системы, инвариантные к сдвигу (ЛИС-системы).
Закончив краткий обзор принципов классификации систем, сконцентрируем внимание на простейшем их виде — линейных стационарных системах с сосредоточенными параметрами
Линейность и инвариантность к сдвигу являются независимыми свойствами системы; ни одно из этих свойств не подразумевает обязательного наличия другого. Например, пространственное маскирование
L [x (n1, п2)] = с(п1, п2) х(п1, п2)
приводящее к умножению входной последовательности на с(п1, п2), линейно, но не инвариантно к сдвигу.
С другой стороны, система
Т [х(n1, n2)] = [х(n1, n2)]2
инвариантна к сдвигу, но не линейна.
Эти системы отличаются простотой, как при разработке, так и при анализе, но в то же время они обладают достаточными возможностями для решения многих практических задач - это наиболее часто изучаемый класс систем для обработки дискретных сигналов любой размерности. Поведение этих систем во многих случаях можно изучать безотносительно к конкретным характеристикам входного сигнала. Разработана достаточно полная теория анализа на основе принципа суперпозиции(нахождение выходной реакции по входному воздействию и системному оператору или нахождение неизвестного входного воздействия по известной выходной реакции и системному оператору) и множество методик конструктивного синтеза систем (определить структуру и внутренние параметры системы по требуемому системному оператору).
|
|
|
Далее будут рассматриваться только линейные стационарные системы, если не оговорено иного.
|
|
|
