 |
Устойчивость динамических систем
|
|
|
|
По определению, линейная динамическая система называется устойчивой, если все ее собственные колебания затухают во времени. Необходимым и достаточным условием устойчивости системы является отрицательность вещественных частей всех корней характеристического уравнения (8.36).
Эти корни не должны быть также и чисто мнимыми. Хотя при этом собственные колебания есть гармонические функции вида
небольшие случайные изменения параметров системы могут привести к переходу ее в неустойчивый режим, когда
представляют собой экспоненциально нарастающие по амплитуде колебания.
Если порядок динамической системы достаточно высок, то прямая проверка устойчивости, основанная на поиске корней характеристического уравнения, может оказаться весьма затруднительной. Поэтому были разработаны специальные критерии устойчивости, позволяющие определять наличие корней с положительными вещественными частями непосредственно по виду коэффициентов, минуя само решение характеристического уравнения (см. гл. 14).
Возникновение нарастающих собственных колебаний в электрических цепях возможно лишь тогда, когда в составе цепи, помимо пассивных элементов L, С, R, содержатся активные элементы, передающие в цепь часть энергии от внешних источников. Распространенной моделью такого активного элемента служит резистор с отрицательным сопротивлением.
Методы анализа прохождения радиотехнических сигналов через линейные стационарные системы во временной и спектральной области
Анализ во временной области
Импульсная характеристика
Пусть некоторая линейная стационарная система описывается оператором Т. Для простоты будем полагать, что входной и выходной сигналы одномерны. По определению, импульсной характеристикой системы называется функция h(t), являющаяся откликом системы на входной сигнал δ(t). Это означает, что функция h(t) удовлетворяет уравнению
|
|
|
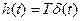. (5)
Поскольку система стационарна, аналогичное уравнение будет и в случае, если входное воздействие смещено во времени на производную величину t0:
(6)
Следует ясно представить себе, что импульсная характеристика, так же как и порождающая ее дельта-функция, есть результат разумной идеализации. С физической точки зрения импульсная характеристика приближенно отображает реакцию системы на входной импульсный сигнал произвольной формы с единичной площадью при условии, что длительность этого сигнала пренебрежимо мала по сравнению с характерным временным масштабом системы, например периодом ее собственных колебаний.
Интеграл наложения. Зная импульсную характеристику линейной стационарной системы, можно формально решить любую задачу о прохождении детерминированного сигнала через такую систему. Входной сигнал всегда допускает представление вида
.
Отвечающая ему выходная реакция
(7)
Теперь примем во внимание, что интеграл есть предельное значение суммы, поэтому линейный оператор Т на основании принципа суперпозиции может быть внесен под знак интеграла. Далее, оператор Т «действует» лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования τ. Поэтому из выражения (7) следует, что
,
или окончательно
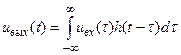(8)
Эта формула, имеющая фундаментальное значение в теории линейных систем, называется интегралом Дюамеля. Соотношение (8) свидетельствует о том, что выходной сигнал линейной стационарной системы представляет собой свертку двух функций — входного сигнала и импульсной характеристики системы. Очевидно, формула (8.8) может быть записана также в виде
|
|
|
(9)
Итак, если импульсная характеристика h(t) известна, то дальнейшие этапы решения сводятся к полностью формализованным операциям.
Легко видеть, что для физически реализуемой системы верхний предел в формуле интеграла Дюамеля может быть заменен на текущее значение времени:
(13)
Формула (13) имеет ясный физический смысл: линейная стационарная система, выполняя обработку поступающего на вход сигнала, проводит операцию взвешенного суммирования всех его мгновенных значений, существовавших «в прошлом» при — ∞ < τ < t. Роль весовой функции выполняет при этом импульсная характеристика системы. Принципиально важно, что физически реализуемая система, ни при каких обстоятельствах не способна оперировать «будущими» значениями входного сигнала.
Такие системы полезны при обработке сигналов, для которых в качестве независимой переменной выступает время, поскольку указанное ограничение физически обосновано и к тому же позволяет создавать системы, работающие в реальном масштабе времени.
Если сигнал представлен дискретными отсчетами, то (9) можно записать в следующем виде
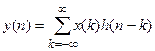
если произвести замену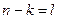 
, то выражение дискретной свертки можно записать в следующем виде
Например, для двумерная дискретная свертка
Импульсный отклик на произвольно расположенный входной импульс равен сдвинутому импульсному отклику на входной импульс, расположенный в начале координат.
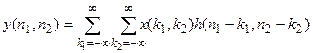
Это соотношение известно под названием двумерной дискретной свертки.
ЛИС-система преобразует каждый импульс в сдвинутую копию импульсного отклика h(n1, n2). Суперпозиция этих взвешенных и сдвинутых импульсных откликов образует выходную последовательность, причем весовыми коэффициентами являются значения отсчетов входной последовательности х(n1, n2).
Выполнив замену переменных 
равенство () можно записать в другой форме:
(Зная импульсную характеристику линейной стационарной системы, можно формально решить любую задачу о прохождении детерминированного сигнала через такую систему. Входной сигнал всегда допускает представление вида
.
Отвечающая ему выходная реакция
(7)
Теперь примем во внимание, что интеграл есть предельное значение суммы, поэтому линейный оператор Т на основании принципа суперпозиции может быть внесен под знак интеграла. Далее, оператор Т «действует» лишь на величины, зависящие от текущего времени t, но не от переменной интегрирования τ. Поэтому из выражения (7) следует, что
|
|
|
,
или окончательно
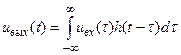(8)
Эта формула, имеющая фундаментальное значение в теории линейных систем, называется интегралом Дюамеля. Соотношение (8) свидетельствует о том, что выходной сигнал линейной стационарной системы представляет собой свертку двух функций — входного сигнала и импульсной характеристики системы.) – лишнее удалить.
Условие физической реализуемости (принцип казуальности). Каков бы ни был конкретный вид импульсной характеристики физически осуществимой системы(казуальной), всегда должен выполняться важнейший принцип: выходной сигнал, отвечающий импульсному входному воздействию, не может возникнуть до момента появления импульса на входе.
Отсюда вытекает очень простое ограничение на вид допустимых импульсных характеристик:
при t<0. (12)
Для большинства двумерных систем независимые переменные не связаны с временем, и казуальность не является естественным ограничением для таких систем. Однако при рассмотрении реализации систем мы вынуждены обратиться к обобщению понятия физически реализуемой системы.
Импульсный отклик h (n) физически реализуемой одномерной ЛИС-системы равен нулю при n<0. Соответственно обобщением понятия физической реализуемости может быть требование, чтобы импульсный отклик был равен нулю вне некоторой опорной области.
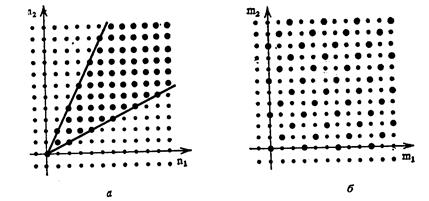
Рис. 3. а — последовательность с опорной областью в виде сектора; б — последовательность с опорной областью в виде квадранта, полученная из последовательности а путем линейного преобразования переменных при значениях(ЛГ,,,ЛГ21) = (2,1) и (ЛГ«,Na) = = (1,2); маленькие кружки обозначают отсчеты с нулевыми значениями.
Условие устойчивости физической системы. Физически реализуемая система должна быть, кроме того, устойчивой, представляют интерес лишь устойчивые системы.Естественно, например, потребовать, чтобы при ограниченной входной последовательности выходная последовательность была также ограничена. Чтобы отличить этот тип устойчивости от других, будем называть такие системы системами с ограниченными входом и выходом (ОВВ-системами). Необходимым и достаточным условием принадлежности ЛС-системы к классу ОВВ-систем является абсолютная суммируемость ее импульсного отклика
|
|
|
. (14)
Многомерная устойчивость значительно сложнее одномерной и для понимания, и с точки зрения испытаний системы на устойчивость.
Свойства свертки
Будем использовать одиночная звездочка (*) для обозначения одномерную свертки, двойная звездочка (* *) будет обозначать двумерную свертку.
Одним из достоинств линейных инвариантных к сдвигу систем является простота анализа соединенных друг с другом систем.
Частично это связано со свойствами оператора свертки. Мы уже видели, что свертка обладает свойством коммутативности:
у = х**h = h**х.
Свертка обладает также свойствомассоциативности. Если результат свертки х и h свернуть с g, результат будет тем же, что и при свертке х с результатом свертки h и g:
(х ** h) ** g = х ** (h ** g).
В силу свойства ассоциативности при описании многократной свертки скобки можно опускать.
Наконец, свертка обладает свойством дистрибутивности по отношению к операции сложения
х**(h + g) = (x**h) + (x**g).
Ассоциативные и дистрибутивные свойства оператора свертки достаточно наглядны. Две системы считаются соединенными последовательно, или каскадно, если выходной сигнал первой системы служит входным сигналом для второй, как это показано на рис. 1.
Если две системы линейны и инвариантны к сдвигу, то, как можно показать, их каскадное соединение также линейно и инвариантно к сдвигу. Если w обозначает выходной сигнал первой системы каскада, то
w = х * * h,
у = w ** g = (х ** h) ** g.
С учетом свойства ассоциативности выражение (1.49) можно переписать следующим образом:
у = х**(h ** g).
Рис.1. -Каскадное соединение двух систем.
Если обе системы линейны и инвариантны к сдвигу, порядок систем в каскаде не имеет значения, и с точки зрения преобразования входного сигнала в выходной обе схемы эквивалентны.
Отсюда эквивалентный импульсный отклик каскадной системы hэкв имеет вид
hэкв = h ** g.
Продвинувшись еще на шаг и использовав правило коммутативности, получим, что эквивалентный импульсный отклик не изменяется, если системы в каскаде поменять местами. Таким образом, две каскадные ЛИС-системы, которые отличаются только порядком входящих в них подсистем, а в остальном идентичны, являются эквивалентными; они формируют одинаковые выходные сигналы при возбуждении одним и тем же входным сигналом.
|
|
|
На рис. 2 показаны две системы, соединенные параллельно. У них общий вход, и общий выходной сигнал формируется путем суммирования выходных сигналов систем. Можно непосредственно доказать, что если обе эти системы линейны и инвариантны к сдвигу, то вся система в целом также линейна и инвариантна к сдвигу. Для нахождения эквивалентного импульсного отклика заметим, что
у = (х** р) + (х**g).
Применив правило дистрибутивности,получим
y = х**(h + g),
откуда следует, что
hЭKB = h + g.
Это правило очевидным образом обобщается на параллельное соединение более двух ЛИС-систем.
Рис. 2. - Параллельное соединение двух систем
Иногда оказывается полезным разложить импульсный отклик на несколько компонент, в частности если импульсный отклик имеет хотя и ограниченную, но причудливой формы опорную область, которую можно представить комбинацией меньших по размеру областей более правильной формы. В этом случае входную последовательность можно свернуть с импульсными откликами — компонентами и получить искомую выходную последовательность (суммируя результаты). В результате путем параллельного соединения более простых систем образуется интересующая нас система.
Переходная характеристика
Пусть на входе линейной стационарной системы действует сигнал, изображаемый функцией Хевисайда σ(t).
Выходную реакцию
(15)
принято называть переходной характеристикой системы. Поскольку система стационарна, переходная характеристика инвариантна относительно временного сдвига:
.
Высказанные ранее соображения о физической реализуемости системы полностью переносятся на случай, когда система возбуждается не дельта-функцией, а единичным скачком. Поэтому переходная характеристика физически реализуемой системы отлична от нуля лишь при t >=0, в то время как g(t)=0 при t < 0.
Между импульсной и переходной характеристиками имеется тесная связь. Действительно, так как
, то на основании (5)
Оператор дифференцирования d/dt и линейный стационарный оператор Т могут меняться местами, поэтому
(16)
Интеграл Дюамеля
Спектральный анализ
|
|
|
