 |
Фазовый сдвиг и групповое время задержки
|
|
|
|
Спектральный метод
Говоря о спектральном методе анализа прохождения, радиотехнических сигналов через линейные стационарные системы, обычно имеют в виду целый комплекс математических приемов, в основе которых лежит использование свойств частотного коэффициента передачи системы. Ниже на конкретных примерах показано применение спектрального подхода как к задаче нахождения реакции системы, так и к проблеме числовой оценки выходного сигнала.
Основная формула. Пусть на входе некоторой линейной стационарной системы действует детерминированный сигнал 
, заданный обратным преобразованием Фурье:
.
Будем полагать, что известен частотный коэффициент передачи К(jω) системы. Как было доказано, комплексный сигнал вида exp(jωt), являясь собственной функцией системного оператора, создает на выходе элементарную реакцию К(jω)exp(jωt). Суммируя эти реакции, находим представление выходного сигнала:
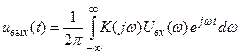(8.48)
Получена основная формула спектрального метода, свидетельствующая о том, что частотный коэффициент передачи системы служит множителем пропорциональности между спектральными плотностями сигналов на входе и выходе:
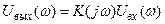(8.49)
Итак, анализ систем в частотной области отличается замечательной чертой — эффект преобразования сигнала в системе отображается просто алгебраической операцией умножения.
Следует иметь в виду, что спектральный и временной подходы полностью эквивалентны друг другу. Действительно, интеграл Дюамеля (8.8) есть свертка функции и импульсной характеристики h(t) во временной области:
.
Значит, спектральная плотность выходного сигнала есть произведение спектральных плотностей функций и h(t). Отсюда непосредственно следует формула (8.49).
|
|
|
Практическая ценность спектрального метода нахождения выходной реакции в каждом конкретном случае зависит от того, удается ли провести интегрирование в формуле (8.48).
Пример. Частотный коэффициент передачи напряжения RC-цепи, схема которой приведена в примере 8.7.
Здесь
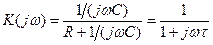
где τ = RС-постоянная времени.
Уравнение АЧХ принимает вид
ФЧХ определяется следующим образом:
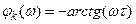
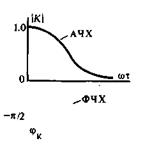
Вид АЧХ указывает на то, что такая цепь может использоваться в качестве фильтра нижних частот (ФНЧ).
Пример 8.12. Частотный коэффициент передачи напряжения Г-образного четырехполюсника, собранного из элементов L, С, R:
и уравнение ФЧХ
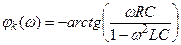
Если сопротивление потерь R достаточно мало, так что добротность системы 
, то данная цепь может с успехом выполнять роль полосового фильтра.
Дискретные системы
Реализация дискретных систем
Рекурсивная структура
Алгоритм работы дискретного частотно селективного фильтра с бесконечной импульсной характеристикой (БИХ) описывается линейным разностным уравнением, которое эквивалентно дифференциальному уравнению для линейных динамических систем.
Дискретный фильтр суммирует (с весовыми коэффициентами) некоторое количество входных отсчетов (включая последний) и некоторое количество предыдущих выходных отсчетов:
,
где aj и bi – вещественные коэффициенты.
Такой фильтр называется рекурсивным.
Получающаяся при этом структура показана на рис. 6.
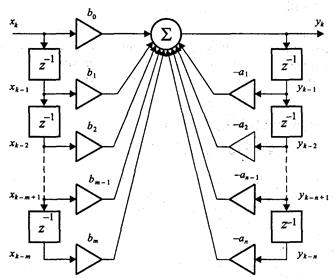
Рис.6. Рекурсивный фильтр — прямая реализация
Так как при вычислениях используются предыдущие отсчеты выходного сигнала, в схеме присутствуют обратные связи.
ЗАМЕЧАНИЕ--------------------------------------------------------------------------------------------------
Количество предыдущих входных и выходных отсчетов, используемых для вычислений, может не совпадать. В таком случае порядком фильтра считается максимальное из чисел m и n.
|
|
|
Импульсная характеристика рекурсивного фильтра рассчитывается значительно сложнее, чем для нерекурсивного. Рассмотрим формирование лишь нескольких первых ее отсчетов. При поступлении на вход единичного импульса он умножается на b0 и проходит на выход. Таким образом,
.
Далее входной единичный импульс попадает во входную линию задержки, а выходной отсчет, равный b0, — в выходную линию задержки. В результате второй отсчет импульсной характеристики будет формироваться как
.
Продолжив рассмотрение перемещения входного единичного импульса вдоль входной линии задержки и заполнения выходными отсчетами выходной линии задержки, можно получить
Видно, что по мере того, как выходная линия задержки заполняется отсчетами импульсной характеристики, сложность аналитических формул быстро возрастает.
Наличие в схеме обратных связей позволяет получить бесконечную импульсную характеристику, поэтому рекурсивные фильтры называют также фильтрами с бесконечной импульсной характеристикой (БИХ-фильтрами; английский термин — infinite impulse response, IIR). По этой же причине рекурсивные фильтры могут быть неустойчивыми.
Иногда используют только рекурсивную часть фильтра.
Применяют и другие структуры вычисления по указанным выражениям, позже они будут рассмотрены.
Для расчета коэффициентов существует большое количество различных методик.
Нерекурсивная структура
При ограниченной импульсной характеристике системы(цепи) для вычисления выходной реакции по интегралу Дюамеля используется его прямая реализация
.
Структурная схема, реализующая этот алгоритм, приведена на рис. 4.
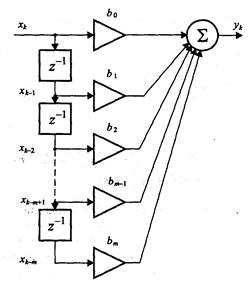
Рис. 4. Нерекурсивный фильтр
Некоторое количество предыдущих отсчетов входного сигнала хранится в ячейках памяти, которые образуют дискретную линию задержки. Эти отсчеты умножаются на коэффициенты biи суммируются, формируя выходной отсчет y(k).
Количество используемых предыдущих отсчетов т называется порядком фильтра.
ЗАМЕЧАНИЕ ---------------------------------------------------------------------------------------
Согласно свойствам z-преобразования, задержка дискретной последовательности на один такт соответствует умножению ее z-преобразования на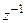 
.Поэтому элементы памяти, осуществляющие такую задержку, обозначены на структурной схеме как «».
|
|
|
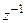Так как при вычислениях не используются предыдущие отсчеты выходного сигнала, в схеме отсутствуют обратные связи. Поэтому такие фильтры называются нерекурсивными (nonrecursive). Применяется также термин «трансверсальный фильтр» (от английского transversal — поперечный).
Импульсная характеристика нерекурсивного фильтра определяется очень просто. Подставим в уравнение (4.15) единичный импульс x0(k) в качестве входного сигнала:
.
Но отсчет x0(k-i) равен нулю для всех k, кроме k = i, когда этот отсчет равен единице. Поэтому мы получаем очень простой результат:
h(k)=bk
то есть коэффициенты bi являются отсчетами импульсной характеристики фильтра. Это можно наглядно пояснить с помощью рис. 5.
Рис 5
При подаче на вход единичного импульса он будет перемещаться по линии задержки, умножаться на коэффициенты b0, b1, b2,... и проходить на выход устройства (ведь все остальные входные сигналы сумматора при этом равны нулю). Очевидно, что в реальном устройстве линия задержки содержит конечное число элементов, поэтому импульсная характеристика нерекурсивного фильтра также является конечной по длительности. Это обусловило еще одно название таких фильтров — фильтры с конечной импульсной характеристикой (КИХ-фильтры; английский термин — finite impulse response, FIR).
Частотная характеристика фильтра легко определяется через дискретное преобразование Фурье
Коэффициент передачи - модуль ЧХ.
ЗАМЕЧАНИЕ -------------------------------------------------------------------------------------------------------
Нерекурсивные цифровые фильтры не являются динамическими системами и устойчивы при любом выборе коэффициентов. Вследствие отсутствия обратных связей любой нерекурсивный фильтр является устойчивым — ведь каковы бы ни были начальные условия (то есть отсчеты, хранящиеся в линии задержки), при отсутствии сигнала на входе (x(k) = 0) выходной сигнал (свободные колебания) будет отличен от нуля в течение не более чем т тактов, необходимых для очистки линии задержки.
|
|
|
Простота анализа и реализации, а также наглядная связь коэффициентов фильтра с отсчетами его импульсной характеристики и абсолютная устойчивость привели к тому, что нерекурсивные фильтры широко применяются на практике. Однако для получения хороших частотных характеристик (например, полосовых фильтров с высокой прямоугольностью АЧХ) необходимы нерекурсивные фильтры высокого порядка — до нескольких сотен и даже тысяч.
|
|
|
