 |
Ход частотной характеристики дискретного фильтра в промежутках между известными равноотстоящими точками
|
|
|
|
Пусть весовые коэффициенты (отсчеты импульсной характеристики) КИХ-фильтра равны g(n), где n=0…N-1, и отсчеты эти располагаются по времени симметрично относительно t=0; при этом моменты отсчетов описываются формулой (316)
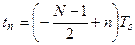
Частотная характеристика фильтра G(f) - это преобразование Фурье его импульсной характеристики. В данном случае
(318)
Используя формулу обратного дискретного преобразования Фурье (92), находим
(319)
В нашем случае коэффициент а, показывающий положение начального импульса последовательности g(n), определяется соотношением а = -(N-1)/2. Частота f1 входящая в (319), —это величина, обратная длительности импульсной характеристики f1=1/T1. Учитывая эти соотношения и формулу (317), подставляем (319) в (318). В результате получаем
(320)
Меняя порядок суммирования и вводя обозначение G(kf1)= GД(k), преобразуем это соотношение:
(321)
Внутреннюю сумму в (321) можно определить как сумму геометрической прогрессии по формуле 
. В результате после несложных преобразований получим окончательно
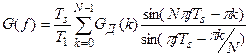. (322)
Соотношение (322) дает возможность определить ход ЧХ КИХ-фильтра в промежутках между равноотстоящими выборками G(kf1).
Оптимальные методы
Оптимальные методы, в которых численными итерационными методами ищется минимум заданной функции качества.
Чаще всего отправной точкой при расчете фильтра служит его желаемая частотная характеристика — либо АЧХ (когда фазовые характеристики не важны), либо комплексный коэффициент передачи. В качестве минимизируемой меры отклонения характеристики фильтра от заданной в общем случае используется р-норма ошибки. Такая норма Lp для функции f(x), определенной на интервале от a до b, рассчитывается следующим образом:
|
|
|
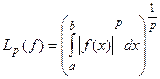
При р=2 норма L2 пропорциональна среднеквадратическому значению функции. При норма Lx дает максимальное (по модулю) значение функции, достигаемое на рассматриваемом интервале. При р=∞ рассматриваемая норма ошибки равна максимальному абсолютному отклонению характеристики от заданной. Минимизация этой нормы соответствует минимаксной аппроксимации (minimax approximation) и дает фильтры с равномерными пульсациями АЧХ (equiripple filter). Для минимаксного синтеза нерекурсивных фильтров используется метод чебышевской аппроксимации с использованием алгоритма многократной замены Ремеза.
Поскольку корень р-й степени при любом р является монотонно возрастающей функцией, при расчете минимизируемой величины его можно не вычислять.
Использование весовой функции позволяет придать разную значимость различным участкам частотной оси. В частности, это дает возможность задать переходные зоны, поведение АЧХ в которых не имеет значения. В этих зонах значение весовой функции должно быть нулевым.
В общем случае задача не имеет аналитического решения и поэтому должна решаться итерационными численными методами. Минимизация ошибки приводит к появлению больших выбросов АЧХ при попытке аппроксимировать ее скачкообразное изменение. Это связано с явлением Гиббса. Для уменьшения влияния эффекта Гиббса при этом может использоваться наложение ограничений на предельное абсолютное отклонение частотной характеристики от заданной.
Восстановление сигналов (решение обратной задачи)
Искажения
Одномерных сигналов
Восстановление сигналов
Интеграл свертки представляется выражением
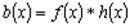(1)
где h(x) - функция, задающая искажение; f(x) - функция, которую необходимо восстановить.
Согласно теореме о свертке фурье-образ величины (1) равен
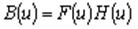(2)
где F(u) - функция, связанная с функцией f(x) двумерным преобразованием Фурье; H(u) - фурье-образ оптической передаточной функции.
|
|
|
Идеализированная задача конечной деконволюции такова: заданы функции b(x) и h(x), требуется восстановить функцию f(x) при условии, что все три величины имеют конечную протяженность.
Из соотношения (2) следует, что эту задачу можно решить следующим образом
(3)
Операция деления внутри фигурных скобок в выражении (3) называется простой инверсной фильтрацией. Термин "фильтрация" здесь употребляется по аналогии с классической теорией цепей и современной теорией обработки сигналов. Классический фильтр представляет собой устройство, которое изменяет спектр временных частот сигнала. Спектр B(u) есть функция пространственной частоты.
Оптическая передаточная функция H(u) изменяет спектр пространственных частот B(u) в результате применения указанной выше операции деления.
Поскольку обработанные изображения обычно хранятся в памяти ЭВМ в виде квантованных значений, в технике обработки изображений, как правило, используются цифровые, а не классические аналоговые фильтры. Цифровой фильтр определяется дискретным массивом, вообще говоря, комплексных чисел, который изменяет в процессе некоторой операции обработки спектр пространственных частот. Следовательно, обе функции, h(x) в формуле (1) и H(u) в формуле (2), могут рассматриваться как фильтры (и в большей части приложений они реализуются в цифровом виде). Общепринятая классификация цифровых фильтров возникла в теории обработки сигналов как функций времени, и этой классификацией можно пользоваться в теории обработки одномерных изображений, т. е. сигналов как функций (одной) пространственной переменной. Мы перенесем соответствующую терминологию на двумерный случай. Понятие "отсчета" в теории обработки сигналов переходит в понятие "элемента изображения" в теории обработки изображений. Как отсчеты, так и элементы изображений должны квантоваться по амплитуде до их цифровой обработки. Изображение, к которому должна быть применена операция фильтрации, называется заданным изображением, и о нем говорят как о состоящем из заданных элементов изображения. Элементы профильтрованного изображения называются выходными элементами изображения.
|
|
|
В случае нерекурсивного цифрового фильтра каждый выходной элемент изображения представляет собой взвешенную сумму заданных элементов изображения.
В случае же рекурсивного цифрового фильтра каждый выходной элемент изображения есть взвешенная сумма заданных элементов изображения и рассчитанных ранее выходных элементов изображения. Все практически реализуемые цифровые фильтры, конечно, описываются массивами конечных размеров (в одномерном случае конечный фильтр часто называют коротким). Цифровой фильтр называется прямым, если он применяется в плоскости изображения, и спектральным - если он применяется в частотной плоскости.
Каузальный фильтр является односторонним в том смысле, что его отклик всегда отстает от входного воздействия (это несколько искусственно в двумерном случае, но, конечно, имеет очень важное значение для операций одномерной фильтрации, которые лежат в основе обработки сигналов как функций времени).
Каузальные фильтры почти всегда реализуются как прямые.
Мультипликативный цифровой фильтр представляет собой спектральный фильтр, в котором каждый выходной отсчет получается как произведение заданного элемента входного сигнала на один элемент массива фильтра.
Решение задачи деконволюции заключается в обращении двумерной свертки. Термин "деконволюция" охватывает наиболее важные и широко используемые методы обработки изображений. Необходимость в такой операции возникает во всех областях науки, связанных с измерениями. По методах деконволюции существует большое число работ [1].
Задача деконволюции может быть решена несколькими способами. Выбор наиболее подходящего для решения этой задачи метода зависит от ряда факторов, в том числе от формы и протяженности функции распространения точки (ФРТ), характера исходного изображения и степени усечения его кадровым окном записывающего устройства.
Существуют различные подходы к задаче деконволюции. Эти подходы включают нерекурсивный и рекурсивный методы фильтрации в плоскости изображения, прямые матричные методы и методы максимальной энтропии и максимального правдоподобия.
|
|
|
Одним из наиболее важных практических методов деконволюции является метод слепой деконволюции.
Кроме известных традиционных приложений деконволюции существуют и различные ее экзотические применения. Одно из наиболее замечательных таких применений - восстановление методом слепой деконволюции записей голосов знаменитых певцов на старых граммофонных пластинках.
|
|
|
