 |
Округление промежуточных результатов вычислений
|
|
|
|
При реализации различных алгоритмов обработки сигналов в процессе вычислений формируется множество промежуточных результатов. Формат хранения этих результатов зачастую вынуждает округлять их, что приводит к появлению дополнительных погрешностей. Операции, при которых появляются эти погрешности, зависят от способа представления чисел, используемого в вычислительном устройстве.
При использовании арифметики с фиксированной запятой операции сложения и вычитания не приводят к необходимости округления результатов — они могут вызвать лишь переполнение.
А вот для представления целой части суммы нужно три разряда, тогда как для слагаемых было достаточно двух. Поэтому, если для представления целой части чисел используется два разряда, в данном случае возникнет переполнение.
В отличие от сложения умножение чисел с фиксированной запятой приводит к увеличению числа значащих цифр результата (по сравнению с сомножителями) и, следовательно, к необходимости округления.
Результат умножения в данном примере имеет 6 значащих цифр после запятой. Если для представления результата используется тот же формат, что и для сомножителей, придется производить округление:
11,10011100 ≈ 11,1010 3.609375 ≈ 3.625
Если для представления чисел используется формат с плавающей запятой, все сказанное об умножении сохраняет силу. Впрочем, если результат умножения по модулю не превосходит единицы, использование формата с плавающей запятой даст большую точность, поскольку не будут зря тратиться разряды для представления незначащих нулей слева.
Однако операции сложения в формате с плавающей запятой тоже могут приводить к потере точности. Пусть рассматриваемые нами два числа представлены в формате с плавающей запятой, использующем 6 разрядов для хранения дробной части нормализованной мантиссы (мантисса и порядок записаны в двоичной системе счисления):
|
|
|
При сложении чисел с плавающей запятой может не выполняться свойство ассоциативности — результат суммирования нескольких чисел может зависеть от последовательности выполнения сложений. При обучении программированию обычно дается рекомендация складывать числа, начиная с меньших (по модулю) и заканчивая самыми большими. Однако при реализации алгоритмов цифровой обработки сигналов мы, как правило, лишены возможности произвольно менять последовательность суммирования (хотя бы потому, что для сортировки слагаемых потребуется дополнительное время).
Для статистического анализа ошибок округления в структурную схему фильтра вводятся эквивалентные источники шума, добавляемого к результатам умножения и (при использовании арифметики с плавающей запятой) сложения. Более подробную информацию об этом можно найти в [8].
Примеры моделирования ошибок округления в цифровом фильтре и при расчете БПФ приведены при описании функций qfilt и qfft пакета Filter Design.
Предельные циклы
Ошибки округления при вычислениях в цифровых фильтрах могут приводить к еще одной очень серьезной неприятности — появлению так называемых предельных циклов (limit cycle), когда вроде бы устойчивый фильтр начинает демонстрировать неустойчивое поведение.
Поясним это явление на простейшем примере, взятом из [8]. Пусть имеется рекурсивный фильтр первого порядка, описываемый разностным уравнением
y(k) =x(k) + 0,95y(k - 1).
Единственный полюс функции передачи данного фильтра, равный 0,95, находится внутри единичной окружности, что свидетельствует об устойчивости фильтра. Пусть входной сигнал отсутствует (x(k) - 0), а внутреннее состояние фильтра, которое в данном случае представляется единственным числом y(0), равно 13. При точных вычислениях сигнал на выходе фильтра экспоненциально затухает:
|
|
|
y(l) = 0,95 y(0) = 0,95 • 13 = 12,35,
y(2) = 0,95 y(1) = 0,95 • 12,35 = 11,7325,
y(3) = 0,95 y(2) = 0,95 • 11,7325 = 11,145875,
y(4) = 0,95 y(3) = 0,95 • 11,145875 = 10,58858125,
y(5) = 0,95 y(4) = 0,95 • 10,58858125 = 10,0591521875,
…
А теперь будем считать, что в ячейке памяти фильтра значение хранится в целочисленном формате и после выполнения умножения используется округление (будем обозначать его квадратными скобками). Выходной сигнал радикально изменится:
у(1) = [0,95 y(0)] = [0,95 • 13] = [12,35] = 12,
y(2) = [0,95 у(1)] = [0,95 • 12] = [11,4] = 11,
y(3) = [0,95 y(2)] = [0,95 • 11] = [10,45] = 10,
y(4) = [0,95 y(3)] = [0,95 • 10] = [9,5] = 10,
y(5) = [0,95 y(4)] = [0,95 • 10] = [9,5] = 10,
…
Итак, выходной сигнал фильтра «залипает» на значении 10 и далее не меняется. Это и есть простейший случай предельного цикла (с периодом, равным единице).
Если в разностном уравнении фильтра изменить знак у коэффициента 0,95, мы получим предельный цикл с периодом, равным двум, в виде чередования значений 10 и -10. В фильтрах более высокого порядка могут возникать предельные циклы с разным периодом.
Различают две разновидности предельных циклов:
- «зернистые» (granular) предельные циклы возникают, когда значения внутреннего состояния фильтра при отсутствии входного сигнала затухают, но из-за ошибок округления не доходят до нуля. Именно такой цикл наблюдается в приведенном примере;
- «переполняющие» (overflow) предельные циклы имеют место в том случае, когда из-за вычислительных погрешностей значения внутреннего состояния фильтра при отсутствии входного сигнала не затухают, а возрастают, вызывая переполнение.
Для анализа возможностей возникновения предельных циклов используется понятие эффективных значений коэффициентов знаменателя функции передачи фильтра. Под эффективным значением коэффициента понимается отношение округленного результата умножения к использованному в качестве множителя значению внутреннего состояния фильтра. Эффективное значение коэффициента будет разным для разных значений состояния. Если для какого-то внутреннего состояния фильтра набор эффективных значений коэффициентов дает полюс функции передачи, расположенный на единичной окружности, это означает, что данное внутреннее состояние при отсутствии входного сигнала дает предельный цикл.
|
|
|
В нашем примере эффективное значение единственного коэффициента фильтра равно
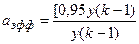 .
.
Построим график значений а эфф для целочисленных значений y(k — 1), лежащих в диапазоне от -20 до 20 (рис. 7.9):
Как видите, если y(k - 1) лежит в диапазоне от -10 до 10, значение a3,M, становится равным единице, а фильтр оказывается на границе устойчивости (полюс функции передачи лежит на единичной окружности), что и приводит к появлению предельного цикла.
В приведенном примере анализ предельных циклов оказывается очень простым, поскольку внутреннее состояние фильтра описывается единственным числом. Для фильтров, степень знаменателя функции передачи которых превышает единицу, анализ базируется на тех же принципах, но оказывается более сложным. Для выполнения такого анализа в пакете Filter Design имеется специальная функция limitcycle, которую мы рассмотрим далее в этой главе.

|
|
|


