Квантование коэффициентов цифровых фильтров

Получая коэффициенты фильтров некоторыми расчетными методами, считали, что они представлены точно. Однако при практической реализации фильтров почти неизбежно возникает необходимость округления их коэффициентов. При использовании цифровых сигнальных процессоров это связано с поддерживаемыми ими форматами представления чисел, при создании программ обработки сигналов для персональных компьютеров — со стремлением повысить быстродействие.

Из-за округления коэффициентов характеристики фильтра претерпевают искажения, величина которых зависит не только от погрешности представления коэффициентов, но и от исходных параметров фильтра и формы его построения (см. раздел «Формы реализации дискретных фильтров» главы 4).

В нерекурсивных фильтрах коэффициенты равны отсчетам импульсной характеристики и линейно связаны с комплексным коэффициентом передачи. Поэтому малые искажения коэффициентов приводят к малым искажениям частотных характеристик и проблемы, связанные с округлением коэффициентов, проявляются редко. Однако, если фильтр должен иметь очень крутой спад АЧХ между полосами пропускания и задерживания, округление коэффициентов все же может привести к заметным искажениям частотных характеристик.

Убедимся в этом на простом примере. Синтезируем методом Ремеза ФНЧ 256-го порядка с полосой пропускания, простирающейся до 0,2, и полосой задерживания, начинающейся от 0,21 (указаны частоты, нормированные к частоте Найквиста). Затем округлим коэффициенты фильтра с точностью до 1/256, оставив в них 8 двоичных разрядов после запятой, и построим графики АЧХ до и после округления (рис. 7.3):

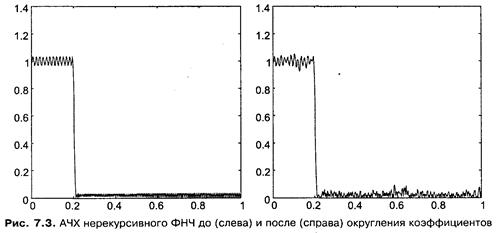
Как видите, ничего особенно страшного не произошло — лишь увеличился размах пульсаций АЧХ. Естественно, в любом случае следует обязательно проконтролировать параметры фильтра после округления коэффициентов, чтобы проверить, удовлетворяет ли квантованный фильтр предъявляемым к нему требованиям.

Значительно серьезнее сказывается округление коэффициентов на характеристиках рекурсивных фильтров, поскольку коэффициенты знаменателя функции передачи связаны с импульсной и частотными характеристиками нелинейно. Как правило, наибольшие искажения происходят в тех случаях, когда АЧХ фильтра имеет крутые скаты в переходных зонах между полосами пропускания и задерживания.

Приведём пример, иллюстрирующий сказанное. Рассчитаем эллиптический ФНЧ 6-го порядка, имеющий частоту среза, составляющую 0,2 от частоты Найквиста, пульсации в полосе пропускания, равные 1 дБ, и уровень пульсаций в полосе задерживания, равный —40 дБ. Напомним, что из всех фильтров, синтезируемых по аналоговым прототипам, именно эллиптические фильтры дают максимальную крутизну спада АЧХ при переходе от полосы пропускания к полосе задерживания. Далее округляем коэффициенты фильтра точно так же, как это делалось в предыдущем примере, и строим графики АЧХ фильтра до и после округления (рис. 7.4):

В данном случае АЧХ изменилась просто катастрофически: в несколько раз увеличилась амплитуда пульсаций коэффициента передачи в полосе пропускания, скат АЧХ стал заметно более пологим, в полосе задерживания исчезли две точки с нулевым коэффициентом передачи.

Теперь посмотрим, что изменится, если мы представим исходный фильтр по-другому — в виде трех последовательно включенных секций второго порядка. В данном случае разница между АЧХ исходного и квантованного фильтра настолько мала, что визуально она не проявляется. Поэтому вместо графиков самих АЧХ построим график их разности (рис. 7.5):

Рисунок 7.5 показывает, что отклонение АЧХ квантованного фильтра от исходной не превосходит , то есть весьма невелико. Таким образом, при представлении фильтра в виде последовательно включенных секций второго порядка округление коэффициентов влияет на характеристики фильтра значительно слабее, чем при прямой форме реализации.

Данный пример демонстрирует общую закономерность, впервые установленную Кайзером [8]: параметры любого фильтра с резким изменением частотной характеристики в переходной полосе, реализованного в прямой форме, крайне чувствительны к значениям коэффициентов фильтра.

Существует два основных подхода к анализу и синтезу фильтров с квантованными коэффициентами.

Можно рассматривать погрешности представления коэффициентов как случайные величины и, задав статистическое описание этих погрешностей, оценить среднеквадратическое отклонение частотной характеристики от исходной.

Второй подход заключается в использовании прямой оптимизации квантованных коэффициентов с целью достижения минимального (в смысле среднеквадратической ошибки или максимального модуля разности) отклонения АЧХ от заданной.