Синтез с использованием окон(Метод взвешивания)

Данный метод предназначен для синтеза нерекурсивных фильтров. Идея его очень проста. Прежде всего находят желаемый комплексный коэффициент передачи в виде непрерывной функции, определенной в диапазоне частот от нуля до частоты Найквиста (если синтезируется вещественный фильтр) или до частоты дискретизации (если проектируется комплексный фильтр). Обратное преобразование Фурье этой характеристики, вычисленное с учетом ее периодического характера, даст бесконечную в обе стороны последовательность отсчетов импульсной характеристики. Для получения реализуемого нерекурсивного фильтра заданного порядка эта последовательность усекается — из нее выбирается центральный фрагмент нужной длины, т.е импульсную характеристику этого БИХ-фильтра g_бих (t) умножают на усредняющее окно g₀(t) и находят импульсную характеристику проектируемого КИХ-фильтра g_ких(t):

g_ких(t) = g _бих (t) * g0(t). (312)

 

Из-за усечения первоначально заданная частотная характеристика искажается.

Умножению импульсных характеристик соответствует свертка частотных характеристик (ЧХ). Если мы хотим, чтобы характеристика, получаемая в результате свертки характеристик БИХ-фильтра и окна, как можно меньше отличалась от ЧХ БИХ-фильтра, то необходимо, чтобы ЧХ окна была по форме близка к δ-импульсу δ(f). Именно такие требования и предъявлялись к ЧХ усредняющих окон: мы считали, что окно тем лучше, чем уже основной лепесток ЧХ в районе нулевой частоты и чем меньше амплитуда боковых лепестков.

 

Простое усечение последовательности отсчетов импульсной характеристики соответствует использованию прямоугольного окна. В результате появляются переходные полосы между областями пропускания и задерживания, наблюдаются колебания коэффициента передачи в полосах пропускания, а в полосах задерживания АЧХ приобретает лепестковый характер.

Для ослабления перечисленных эффектов и прежде всего для уменьшения уровня лепестков в полосах задерживания усеченная импульсная характеристика умножается на весовую функцию (окно), плавно спадающую к краям.

 

В качестве исходных БИХ-фильтров, обладающих требуемыми частотными характеристиками, можно использовать идеальные фильтры. Амплитудно-частотные характеристики идеальных дискретных фильтров показаны на рис. 56. Вид приведенных на этом рисунке кривых определяется следующими обстоятельствами. Во-первых, у идеального фильтра равна нулю ширина переходной зоны между полосой пропускания и полосой заграждения, поэтому все АЧХ на рис. 56 имеют вид прямоугольных импульсов в частотной области. Во-вторых, у фильтров, имеющих вещественную импульсную характеристику, АЧХ обладает четной симметрией. И наконец, в-третьих, АЧХ дискретного фильтра периодически повторяется с периодом, равным частоте дискретизации. Два последних свойства обусловливают четную симметрию АЧХ в частотном промежутке 0— F_s относительно средней частоты F_s/2.

Рис. 56. Амплитудно-частотные характеристики идеальных дискретных фильтров: нижних частот (а), верхних частот (б), полосно-пропускающего (в)

 

Импульсные характеристики, соответствующие идеальным БИХ-фильтрам, можно найти с помощью обратного преобразования Фурье. Периодическим частотным характеристикам, показанным на рис. 56, соответствуют дискретные импульсные характеристики. Для ФНЧ с частотой среза f_с (рис. 56, а) импульсная характеристика имеет вид

 

(313)

Импульсная характеристика ФВЧ, полоса пропускания которого шириной f_ш располагается от F_s/2 - f_ш/2 до F_s/2 + f_ш/2 (рис. 56,6), имеет вид

(314)

т.е. центр полосы пропускания расположен на 0,5 F_s.

Наконец, для полосно-пропускающего фильтра (ППФ), у которого центральная частота полосы пропускания равна f_ц, а ширина этой полосы равна f_ш (рис. 56, в), импульсная характеристика описывается формулой

(315)

 

Рассмотрим два примера проектирования дискретных КИХ-фильтров: фильтра нижних частот и фильтра верхних частот.

Пусть проектируемый ФНЧ имеет частоту среза f_c = 1 кГц. Выберем частоту дискретизации F_s равной 4 кГц. Импульсная характеристика идеального БИХ-фильтра для данного случая показана на рис. 57, а, а его ЧХ—на рис. 57,б. Для взвешивания импульсной характеристики используем окно с числом импульсов N, равным 16 (рис. 57,в), например окно Хана

.

Частотная характеристика, соответствующая этому окну, показана на рис. 57, г.

 

Рис. 57. Весовые функции идеального БИХ-фильтра нижних частот (а), усредняющего окна (в), синтезированного КИХ-фильтра (д) и соответствующие им АЧХ (б, г, е)

 

Далее нам нужно перемножить импульсные характеристики рис. 57, с и б; это будет соответствовать свертке ЧХ рис. 57, б и г. При операции свертки одна из частотных характеристик сдвигается по частоте относительно другой, затем они перемножаются и определяется интеграл этого произведения. Если принять во внимание эти действия, то тогда станет понятно, что ширина основного лепестка ЧХ окна определяет ширину переходной зоны между полосами пропускания и заграждения проектируемого фильтра, а уровень боковых лепестков ЧХ окна определяет пульсации ЧХ этого фильтра в полосе пропускания и в полосе заграждения.

В нашем случае импульсная характеристика исходного идеального БИХ-фильтра определяется по формуле (313) при подстановке в нее

(315)

где n — номер импульса (n изменяется от 0 до N —1).

Произведя операцию взвешивания с помощью окна, получим g_ких(n)=g _бих(n)*g0(n). Полученная ВФ показана на рис. 57, д. АЧХ спроектированного фильтра может быть найдена с помощью ДПФ.

Эта АЧХ в данном случае имеет вид такой, как показано на рис. 57, е. В промежутке от f = 0 до f = 0,7 кГц отклонение АЧХ от единичного значения не превышает 0,24 дБ, а в промежутке f = 1,4 2,6 кГц АЧХ не превосходит значения — 50 дБ. Если требуется, чтобы АЧХ фильтра была более близка к оптимальной, этого можно достигнуть, увеличивая число импульсов ВФ N (в рассмотренном примере N = 16).

Спроектируем теперь ФВЧ с полосой пропускания выше частоты f = 1,5 кГц. Выберем, как и раньше, частоту дискретизации f₂, равную 4 кГц. АЧХ идеального БИХ-фильтра для данного примера показана штриховой линией на рис. 58, с. Будем теперь использовать для взвешивания окно Хэмминга

.

 

 

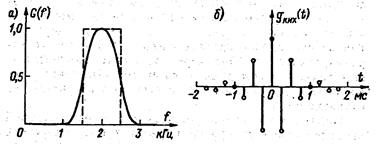
Рис. 58. Частотная характеристика (а) и весовая функция (б) КИХ-фильтра верхних частот

 

При конструировании дискретного КИХ-фильтра верхних частот необходимо выбирать нечетное число импульсов ВФ N. Это объясняется тем обстоятельством, что при четном N значение АЧХ при f = f₂/2 всегда равно нулю.

А в случае фильтра верхних частот при f = f₂/2 мы должны получить значение приведенной АЧХ, равное единице (рис. 58,а). Используя формулы окна Хэмминга, (312), (314) и (316), для проектируемого фильтра получаем

 

(317)

g_ких(n) = g _бих (n) g0(n).

 

Выберем N = 15. Эта весовая функция КИХ-фильтра показана на рис. 58, б, а соответствующая ей АЧХ представлена сплошной кривой на рис. 58, а. Эта АЧХ найдена с помощью ДПФ.

Однако величина боковых лепестков собственного спектра окна не совпадает с величиной лепестков АЧХ фильтра, синтезированного с применением данного окна.

Однако следует помнить о том, что уменьшение уровня боковых лепестков неизбежно приводит к расширению переходной зоны между полосами пропускания и задерживания. Поэтому выбирать весовую функцию следует исходя из требований, предъявляемых к параметрам фильтра.

Метод частотных выборок

Метод частотных выборок предполагает использование обратного дискретного преобразования Фурье (ДПФ) для определения весовых коэффициентов КИХ-фильтра. ДПФ, как известно, позволяет найти равноотстоящие отсчеты спектра ограниченного по времени дискретизированного сигнала. Обратное ДПФ в свою очередь позволяет найти отсчеты сигнала, которые соответствуют заданным отсчетам спектра. Таким образом, мы можем взять желаемую частотную характеристику проектируемого КИХ-фильтра, найти равноотстоящие выборки этой характеристики и затем по ним найти отсчеты импульсной характеристики (весовые коэффициенты) фильтра. Так можно спроектировать фильтр, ЧХ которого гарантированно пройдет через заданные равноотстоящие точки. Однако между этими точками совпадение желаемой и реальной частотных характеристик не гарантируется.

Покажем на примерах, как производится проектирование дискретных КИХ-фильтров методом частотных выборок.

Спроектируем фильтр нижних частот, такой же, как был в примере при рассмотрении метода взвешивания (см. рис. 57, т.е. F_s=4кГц). Желаемая идеальная АЧХ проектируемого фильтра показана штриховой линией на рис. 59, а. Пусть проектируемый КИХ-фильтр будет иметь импульсную характеристику, состоящую из 16, импульсов (N=16).

На идеальной ЧХ, показанной на рис. 59, а, берем выборки, соответствующие частотам , где f_s — частота дискретизации. В нашем случае f_s = 4 кГц и выборки ЧХ будут иметь значения G_Д(0)-…- G_Д(7)= 1; 1; 1; 1; 0,5; 0; 0; 0. Так как ЧХ обладает симметрией относительно , то достаточно взять только N/2=8 выборок.

Следует обратить внимание на то, что выборка, соответствующая частоте f=l кГц (k = 4), попадает на вертикальный спад АЧХ и поэтому мы берем значение G_Д(4) равным 0,5, т. е. полусумме значений ЧХ при подходе слева в справа к данной частоте.

Далее нужно воспользоваться формулой обратного ДПФ для того, чтобы во частотным выборкам G(k) найти отсчеты импульсной характеристики g(n). Здесь подходит любая из двух формул (105) или (109). Этя формулы были выведены в § 14 применительно к ДПФ симметричных сигналов. Импульсные же характеристики проектируемых КИХ-фильтров как раз и представляют собой четно-симметричные функции времени. Отметим, что если бы мы решили проектировать КИХ-фильтр нижних частот с нечетным числом импульсов N, то тогда нужно было бы применять одну из формул (107) или (111).

Рис. 59. Графики, поясняющие метод синтеза КИХ-фильтров, основанный на применении частотных выборок

 

Применим в нашем случае формулу (105). Тогда

,

и мы получим g(0)…g(7) = -0,070; -0,215; 0,378; 0,580; -0,862; -1,323; 2,331; 7,179 (рис. 59,6).

Частотная характеристика, соответствующая этой весовой функции; найденная по формуле (251), показана сплошной линией на рис. 59, а. Эта линия проходит через точки на идеальной частотной характеристике, которые мы использовали в качестве частотных выборок. В промежутках между этими точками ход реальной ЧХ описывается формулой (322).

Спроектируем теперь методом частотных выборок КИХ-фильтр верхних частот с полосой пропускания от 1,5 кГц до f_s/2 = 2 кГц. В качестве исходной берем идеальную частотную характеристику, показанную штриховой линией на рис. 59, в. Выберем f₁=f_s/16. Тогда отсчеты идеальной ЧХ равны следующим значениям: G(0) =... = G(5)==0; G(6) =… = G(10)=0,5; G(7)=G(8)=G(9)=1. Для нахождения весовых коэффициентов КИХ-фильтра можно воспользоваться формулами обратного дискретного преобразования Фурье (107) или (111). Именно для этих вариантов ДПФ обеспечивается четная симметрия отсчетов ЧХ относительно частоты f₂/2, что и требуется в случае фильтра верхних частот.

Выберем Т₂= Т₁/(N-1) и соответственно этому применим формулу (111). Тогда при N=17 и учитывая значения частотных выборок, получим соотношение

По этому соотношению находим g(0)…g(8) = 0; 0,141; -0,414; 0,473; 0; -1,058; 2,414; -3,555; 4 (рис. 59,г). Найденная по формуле (252) ЧХ для этого фильтра имеет вид, показанный на рис. 59, в сплошной линией. Как и в предыдущем примере, эта ЧХ проходит через точки, соответствующие использованным в расчете выборкам идеальной ЧХ, а в промежутках между этими точками ход ЧХ описывается формулой (322).

 

⇐ Предыдущая21222324252627282930Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: