 |
Простейшие аналоговые и цифровые фильтры
|
|
|
|
ФНЧ
ФВЧ
Соответствие интегрированию и дифференцированию.
Взаимосвязь ДПФ и фильтрации
В данном разделе рассматривается, как они связаны друг с другом, причем связь эта оказывается двусторонней — ДПФ можно представить как обработку сигнала набором фильтров, а дискретную фильтрацию можно организовать с помощью ДПФ, что позволяет значительно уменьшить число вычислительных операций за счет использования алгоритмов БПФ.
ДПФ как дискретная фильтрация
Рассмотрев принципы дискретной фильтрации и познакомившись с дискретным преобразованием Фурье, можно заметить, что формулы, описывающие эти два процесса, весьма схожи — в обоих случаях они представляют собой линейную комбинацию отсчетов входного сигнала. Это говорит о том, что ДПФ можно трактовать как обработку сигнала фильтром с соответствующей импульсной характеристикой.
Эту импульсную характеристику можно получить, если заметить, что еj2πn=1 при целочисленном n, и с учетом этого записать формулу прямого ДПФ (5.3) в виде
.
Преобразованная таким способом формула ДПФ представляет собой дискретную свертку (4.3), то есть N-й отсчет результата обработки входного сигнала x(k) фильтром, импульсная характеристика которого равна
Разумеется, импульсная характеристика для каждого частотного отсчета ДПФ своя; чтобы подчеркнуть это, в ее обозначении использован индекс п.
Определим частотную характеристику такого фильтра. Для этого сначала необходимо получить функцию передачи:
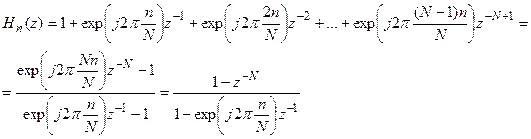.(5.16)
ЗАМЕЧАНИЕ --------------------------------------------------------------------------------------
Для расчета функции передачи использована формула суммы конечной геометрической прогрессии:
.
Для расчета частотной характеристики используем подстановку z = ejωT:
|
|
|
.
АЧХ такого фильтра после несложных тригонометрических преобразований можно записать следующим образом:
, (5.17)
где 
.
Результат показывает, что АЧХ фильтра описывается рассмотренной в разделе «Функции генерации периодических сигналов» главы 3 функцией Дирихле:
K(ω) =diricN (ω - ωn).
На рис. 5.6 показан график АЧХ одного из каналов ДПФ при N = 8 (градуировка частотной оси выполнена в номерах каналов). Пунктирной линией на этом рисунке изображена АЧХ соседнего частотного канала:
Рис. 5.6. АЧХ частотных каналов ДПФ
Как видно из графиков, АЧХ фильтра, реализуемого при вычислении ДПФ, имеет большой уровень боковых лепестков — примерно
При N»1 это выражение стремится к 
-13,5 дБ. Для уменьшения уровня боковых лепестков используют весовые функции, или окна (см. в этой главе далее).
Проектирование дискретных фильтров
Существует довольно много методов расчета дискретных фильтров. Большинство из них основывается на проектировании дискретного варианта соответствующего непрерывного фильтра (прототипа). Существуют также и прямые методы, когда сразу проектируется дискретный фильтр.
Под проектированием (или синтезом) цифрового фильтра понимается выбор таких наборов коэффициентов {а} и {b}, при которых характеристики получающегося фильтра удовлетворяют заданным требованиям. Строго говоря, в задачу проектирования входит и выбор подходящей структуры фильтра с учетом конечной точности вычислений (Эффекты квантования). Это особенно актуально при реализации фильтров «в железе» — с использованием специализированных БИС или цифровых
Используемые методы синтеза цифровых фильтров можно классифицировать следующим образом:
Субоптимальные методы
Субоптимальные методы, не дающие в точности оптимального решения, но позволяющие значительно упростить вычисления по сравнению с оптимальными методами. Как правило, эти методы используют специфику решаемой задачи, например, дробно-рациональный вид функции передачи рекурсивного фильтра или экспоненциальный вид отдельных слагаемых его импульсной характеристики. При этом, в частности, может использоваться тот факт, что коэффициенты числителя функции передачи фильтра линейно связаны с его комплексной частотной характеристикой и потому влияют на ее форму значительно слабее, чем коэффициенты знаменателя. Кроме того, для поиска коэффициентов знаменателя часто используются методы авторегрессионного анализа.
|
|
|
|
|
|
