Синтез и реализация двумерных фильтров

Синтез двумерных цифровых фильтров существенно отличается от синтеза одномерных. В одномерном случае задачи синтеза фильтра и его схемной реализации четко разделены. Сначала выполняется синтез фильтра, а затем с помощью соответствующих преобразований передаточной функции определяются коэффициенты, необходимые для построения конкретной схемной реализации. В двумерном случае ситуация совершенно иная из-за того, что многомерные полиномы в общем случае нельзя разложить на множители. Это значит, что нет возможности в общем случае менять форму произвольной передаточной функции для согласования ее с требованиями схемной реализации. Если мы в состоянии реализовать только передаточные функции, разложимые на множители, то и метод синтеза должен приводить только к фильтрам этого класса. Это обстоятельство усложняет задачу проектирования фильтров и сокращает число практически приемлемых реализаций.

КИХ-фильтр (фильтр с конечной импульсной характеристикой), называемый также нерекурсивным, — это фильтр, импульсный отклик которого содержит лишь конечное число ненулевых отсчетов. Такой импульсный отклик всегда абсолютно суммируем, и, следовательно, КИХ-фильтры всегда устойчивы. КИХ-фильтры имеют также то преимущество, что их работу легче понять как в одномерном, так и в многомерном случае.

БИХ-фильтр (фильтр с бесконечной импульсной характеристикой), или рекурсивный, — это фильтр, входной и выходной сигналы которого удовлетворяют многомерному разностному уравнению конечного порядка. Такие фильтры могут быть как устойчивыми, так и неустойчивыми, однако во многих случаях они оказываются проще в реализации, чем эквивалентные КИХ-фильтры. Синтез двумерного рекурсивного фильтра радикально отличается от синтеза одномерного фильтра. Отчасти это связано с возрастанием сложности обеспечения устойчивости.

КИХ-фильтры

Одно из важнейших преимуществ КИХ-фильтров перед БИХ-фильтрами заключается в возможности синтеза и практической реализации КИХ-фильтров с чисто вещественными частотными откликами. Такие фильтры называются фильтрами с нулевой фазой (Строго говоря, чисто вещественный частотный отклик может содержать отрицательные значения амплитуды на некоторых частотах, что соответствует значению фазы л, а не 0. Несмотря на это, термин «фильтр с нулевой фазой» традиционно включает все чисто вещественные частотные отклики.).

В частотной области условие нулевой фазы можно выразить следующим образом:

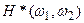= . (3.1)

Выполнив обратное преобразование Фурье от обеих частей равенства (3.1), для импульсного отклика фильтра с нулевой фазой получим требование симметрии в пространственной области

= (3.2)

Очевидно, что КИХ-фильтр может удовлетворять этому условию, если центр его опорной области совпадает с началом координат.

Фильтры с нулевой фазой важны для многих приложений цифровой обработки многомерных сигналов. Например, при обработке изображений фильтры с ненулевой фазой могут привести к разрушению линий и границ. Чтобы понять, почему это так, вспомним из нашего обсуждения преобразований Фурье, что любой сигнал можно представить в виде суперпозиции комплексных синусоид.

Линейный инвариантный к сдвигу фильтр с нетривиальным частотным откликом будет избирательно усиливать или ослаблять некоторые из этих синусоидальных компонент, а также задерживать некоторые компоненты по отношению к другим. На любой частоте величина задержки зависит от значения фазового отклика. Нелинейный фазовый отклик приводит, таким образом, к рассеянию строго согласованных синусоидальных компонент сигнала, составляющих контрастные точки, линии и границы.

Фильтр с нулевой фазой имеет и другие преимущества. В силу вещественности его частотного отклика упрощается синтез фильтра. К тому же симметрию импульсного отклика фильтра можно использовать при его реализации для уменьшения требуемого числа умножений.

Реализация КИХ-фильтров путем прямой свертки. Выходной сигнал любого ЛИС-фильтра можно получить из входного с помощью свертки по формуле скользящего суммирования

Импульсный отклик КИХ-фильтра содержит лишь конечное число ненулевых отсчетов, и пределы суммирования в (3.3) конечны. В этом случае формула скользящего суммирования представляет собой алгоритм, позволяющий вычислить последовательные выходные отсчеты фильтра. Если, например, предположить, что фильтр обладает опорной областью {(n₁, n₂): 0<=n₁<N₁, 0<=N₂}, то для вычисления выходных отсчетов можно воспользоваться соотношением

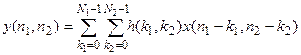
Если в наличии имеются все входные отсчеты, то выходные отсчеты можно вычислять в любом порядке; их можно вычислять и одновременно. Если требуются только определенные отсчеты выходного сигнала, то можно ограничиться вычислением лишь этих отсчетов. Однако для получения каждого выходного отсчета требуется выполнить N₁N₂ умножений и N₁N₂ -1 сложений.

При вычислении используются значения входных отсчетов из N₁-1 «предыдущих» столбцов и N₂-1 «предыдущих» строк. Если входные отсчеты поступают строка за строкой, требуется память, достаточная для хранения N₂ строк входной последовательности. Если, наоборот, на вход поступают столбец за столбцом, необходима память для хранения N₁ входных столбцов.

Фильтр с нулевой фазой с вещественным импульсным откликом удовлетворяет условию 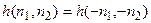, т. е, каждому отсчету соответствует парный ему отсчет с тем же значением. В этом случае, воспользовавшись свойством дистрибутивности сложения, можно поменять местами некоторые операции умножения и сложения в формуле (3.3), чтобы уменьшить их число, однако количество умножений, требуемых для реализации фильтра, все еще остается пропорциональным порядку фильтра.