 |
Свойства ЦФ различной структуры
|
|
|
|
| Структура | |||||
| Характеристика | каскадная | параллельная | волновая | лестничная | частотной выборки |
| Чувствительность к квантованию коэффициентов | Средняя | Средняя | В АУ с фиксированной запятой - средняя, с плавающей - низкая | Высокая | Высокая |
| Уровень шума квантования арифметических операций | Средний | Низкий | Низкий | Высокий | Средний |
| Уровень выходных шумов квантования | Низкий | Средний | Низкий | Высокий | Средний |
| Эффективность вычислений | Высокая | Высокая | Низкая | Высокая | Средняя |
| Возможности распараллеливания и мультиплексирования | Хорошие | Хорошие | Отсутствуют | Средние | Хорошие |
| Возможности сжатия динамического диапазона и масштабирования | Средние | Средние | Низкие | Средние | Хорошие |
Продолжение табл. 4.6
| Структура | |||||
| Характеристика | интерполяционная | Грея-Маркела | на основе Фурье | на основе быстрых преобразований Уолша, Адамара, Хаара | на основе теоретико-числовых преобразований |
| Чувствительность к квантованию коэффициентов | Высокая | Низкая | Средняя | Нулевая | Нулевая |
| Уровень шума квантования арифметических операций | Средний | Высокий | Средний | Средний | Нулевой |
| Уровень выходных шумов квантования | Средний | Высокий | Средний | Низкий | Нулевой |
| Эффективность вычислений | Средняя | Высокая | Высокая | Высокая | Очень высокая |
| Возможности распараллеливания и мультиплексирования | Хорошие | Средние | Хорошие | Хорошие | Очень хорошие |
| Возможности сжатия динамического диапазона и масштабирования | Хорошие | Средние | Хорошие | Хорошие | Очень низкие |
Формы реализации дискретных фильтров
Структурная схема, показанная ранее, называется прямой формой реализации рекурсивного фильтра (direct form I) и не является единственно возможной. Рассмотрим еще несколько вариантов.
|
|
|
Каноническая форма
Разделим общий сумматор в схеме рис. 7 на два отдельных — для рекурсивной и нерекурсивной частей фильтра (рис. 8, а). В результате получаем два последовательно соединенных фильтра, один из которых является нерекурсивным, а другой, напротив, содержит только рекурсивную часть. Так как результат последовательного прохождения сигнала через ряд линейных стационарных устройств не зависит от последовательности их соединения, мы можем поменять местами две «половинки» нашего фильтра (рис. 8, б). Теперь остается заметить, что в обе линии задержки подается один и тот же сигнал, поэтому они будут содержать одинаковые наборы отсчетов. Это позволяет объединить линии задержки. Полученная в результате схема изображена на рис. 9, она называется канонической формой реализации рекурсивного фильтра (canonic form или direct form II).
С теоретической точки зрения эти варианты эквивалентны. Однако при практической реализации необходимо обратить внимание на ряд особенностей, присущих этим схемам. С одной стороны, при канонической реализации используется общая линия задержки, что уменьшает число необходимых ячеек памяти. Однако при этом абсолютные величины отсчетов, «бегающих» в линии задержки, могут существенно превосходить амплитуду входного и выходного сигналов. Это приводит к необходимости увеличивать разрядность представления чисел в линии задержки по сравнению с разрядностью входного и выходного сигналов, что усложняет реализацию устройства. При прямой реализации в линиях задержки хранятся непосредственно отсчеты входного и выходного сигналов, то есть повышенная разрядность линий задержки не требуется. Единственным элементом, требующим повышенной разрядности, в данном случае является сумматор, и это учтено в архитектуре микропроцессоров, специально предназначенных для обработки сигналов в реальном времени.
|
|
|

Рис. 8.Перестановка рекурсивной и нерекурсивной частей фильтра путь к получению канонической реализации
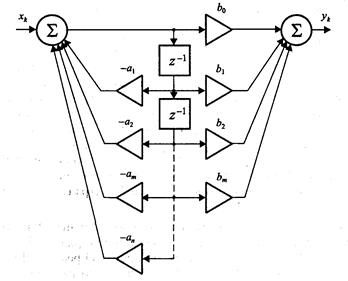
Рис. 9.Рекурсивный фильтр — каноническая реализация
Транспонированная форма
Поменяем в схеме рис. 6 последовательность выполнения операций умножения и задержки, используя в каждой ветви отдельную линию задержки на нужное количество тактов. Разделим также общий сумматор на несколько двух-входовых сумматоров. Получившаяся структура показана на рис. 10. Теперь, рассмотрев любую пару соседних сумматоров, можно заметить, что суммируемые ими сигналы претерпевают некоторую общую задержку. Это дает возможность поменять местами операции суммирования и задержки. Получившаяся схема, показанная на рис. 11, называется транспонированной реализацией дискретного фильтра (direct transposed form II).
ЗАМЕЧАНИЕ--------------------------------------------------------------------------------------------------
Разумеется, в транспонированной форме может быть реализован и нерекурсивный фильтр. Для этого в структурной схеме рис. 10 необходимо удалить все ветви с коэффициентами bt, кроме bo.
Транспонированная схема позволяет эффективно распараллелить вычисления и потому применяется при реализации дискретных фильтров в виде специализированных интегральных схем. Действительно, при реализации фильтра в форме рис. 4.3 или рис 4.4 можно одновременно выполнять все операции умножения, но для получения выходного результата необходимо дождаться окончания выполнения всех операций сложения. В транспонированной же схеме, помимо умножения, можно одновременно выполнять и все операции сложения, поскольку они являются независимыми (то есть не используют в качестве суммируемых величин результаты других сложений).

Рис. 10. Изменение последовательности выполнения операций умножения и задержки — путь к получению транспонированной реализации фильтра
Как видно из схемы рис. 10, собственно для расчета выходного сигнала необходимо выполнить одно умножение и одно cложение; все остальные операций производят подготовку промежуточных результатов для вычисления последующих выходных отсчетов.
|
|
|

Рис. 11.Транспонированная реализация дискретного фильтра
Если применить описанные преобразования к канонической структуре, показанной на рис. 9, получится еще один вариант транспонированной реализации фильтра (direct transposed form I) (рис. 12). В отличие от предыдущей схемы, данная структура содержит большее число элементов памяти.
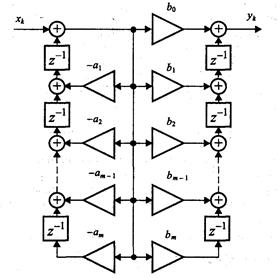
Рис. 12.Транспонированная реализация, полученная из канонической формы дискретного фильтра
|
|
|


