 |
Вторичные параметры однородной линии
|
|
|
|
К вторичным параметрам линии относят коэффициент распространения γ (2.7) и волновое сопротивление Zв (2.9). Они входят во все расчетные соотношения волновых процессов в линии и определяются через первичные параметры r0, L0, g0, С0.
Коэффициент распространения

характеризует изменение амплитуд (действующих значений) и фаз напряжения и тока на единицу длины линии. Его действительная часть α называется коэффициентом затухания, а мнимая часть β – коэффициентом фазы.
Коэффициент затухания определяет уменьшение амплитуды бегущей волны в направлении распространения, существенно зависит от частоты передаваемого сигнала (рис. 2.4), измеряется в неперах на единицу длины линии (Нп/км, Нп/м).

Рис. 2.4. Зависимость коэффициента затухания от частоты
Коэффициент фазы характеризует изменение фазы бегущей волны напряжения или тока на участке, равном единице длины, определяет основные параметры бегущих волн: фазовую скорость Vф (2.12) и длину волны λ (2.13); измеряется в радианах на единицу длины. Частотная зависимость коэффициента фазы приведена на рис. 2.5.
Волновое сопротивление

устанавливает соотношение между комплексными значениями напряжения и

Рис. 2.5. Зависимость коэффициента фазы от частоты
тока прямых и обратных волн в любой точке линии:

Частотная зависимость модуля  и аргумента φВ(ω) волнового сопротивления приведены на рис. 2.6. На нулевой частоте (в линиях постоянного напряжения) волновое сопротивление имеет наибольшее значение. С ростом частоты модуль волнового сопротивления стремится к своему пределу, а аргумент?В > 0. Волновое сопротивление в основном носит емкостный характер.
и аргумента φВ(ω) волнового сопротивления приведены на рис. 2.6. На нулевой частоте (в линиях постоянного напряжения) волновое сопротивление имеет наибольшее значение. С ростом частоты модуль волнового сопротивления стремится к своему пределу, а аргумент?В > 0. Волновое сопротивление в основном носит емкостный характер.

Рис. 2.6. Частотная зависимость модуля и аргумента волнового сопротивления воздушной линии
|
|
|
Расчетные уравнения линии
Коэффициенты  в уравнениях (2.6) и (2.8) определяются из заданных граничных условий: напряжения и тока на входе или выходе линии. На рис. 2.7 показана линия с входными
в уравнениях (2.6) и (2.8) определяются из заданных граничных условий: напряжения и тока на входе или выходе линии. На рис. 2.7 показана линия с входными 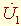 ,
,  и выходными
и выходными  ,
,  значениями напряжений и токов.
значениями напряжений и токов.

Рис. 2.7. Схема длинной линии
При выборе граничных значений в начале линии: x = 0;  из соотношений
из соотношений

определяются коэффициенты

Расчетные уравнения принимают вид:

Полученные выражения позволяют определить напряжение  и ток
и ток  в любой точке линии по заданным значениям
в любой точке линии по заданным значениям 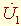 и
и  в начале линии и отсчете координаты х от начала линии.
в начале линии и отсчете координаты х от начала линии.
Уравнения (2.22) после раскрытия скобок и перегруппировки слагаемых преобразуются к уравнениям с гиперболическими функциями:

Часто граничные условия выбирают в конце линии: напряжение  и ток
и ток  (или сопротивление нагрузки
(или сопротивление нагрузки  ). В этом случае отсчет координаты ведется от конца линии и обозначается через y (рис. 2.7). При длине линии l координата х = l – y.
). В этом случае отсчет координаты ведется от конца линии и обозначается через y (рис. 2.7). При длине линии l координата х = l – y.
При выборе граничных условий в конце линии х = l из соотношений:

находятся коэффициенты

Подстановка коэффициентов (2.25) в уравнения (2.6) и (2.8) при замене координаты х = l – y приводит уравнения к окончательному виду:

Первые слагаемые в уравнениях (2.26) – прямые волны соответственно напряжения и тока, вторые слагаемые – обратные волны.
Отношение обратной волны напряжения к прямой в конце линии называется коэффициентом отражения:

Уравнения (2.26) при отсчете координаты у от конца линии преобразуются к уравнениям с гиперболическими функциями:

Согласно уравнениям (2.28) однородную линию длиной l на заданной частоте можно заменить симметричным четырехполюсником с коэффициентами:

Характеристическое сопротивление симметричного четырехполюсника Zc = Zв.Постоянная передачи

|
|
|


