 |
Законы магнитных цепей при постоянных потоках
|
|
|
|
Одним из основных законов, используемых при расчетах магнитных цепей, является закон полного тока
Циркуляция вектора напряженности магнитного поля 
по любому замкнутому контуру равна алгебраической сумме токов 
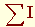, охватываемых этим контуром. Вектор имеет размерность ампер на метр (А/м).
Если контур интегрирования охватывает w витков катушки, через которую проходит ток I, закон полного тока принимает вид:
где F = Iw – магнитодвижущая сила (м.д.с.), или намагничивающая сила (н.с.), измеряемая в амперах (ампер-витках).
Чаще всего контур интегрирования при расчете магнитной цепи выбирается по средней линии магнитопровода, тогда векторное произведение 
заменяется скалярным Hdl, т.к. линия вектора совпадает с контуром интегрирования.
Знак магнитодвижущей силы определяют по мнемоническому правилу охвата катушки правой рукой, расположив пальцы по направлению тока в катушке, при этом отогнутый большой палец показывает направление м.д.с. (рис. 3.3).
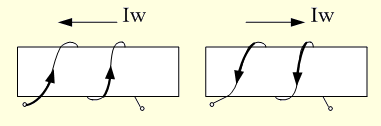
Рис. 3.3. Определение знака магнитодвижущей силы
С вектором напряженности магнитного поля связан вектор магнитной индукции 
, измеряемый в теслах (Тл):
где μ – относительная магнитная проницаемость (безразмерная величина);
μ0 –магнитная постоянная, равна 4π×10-7, Гн/м;
μа – абсолютная магнитная проницаемость, Гн/м.
Через вектор магнитной индукции определяется скалярная величина – магнитный поток Ф, измеряемый в веберах (Вб)
Магнитная цепь, во всех сечениях которой магнитный поток одинаков, называется неразветвленной. Но сечения на разных участках могут быть различны. Принимая равномерное распределение магнитной индукции по сечению, получим на участках разного сечения разные значения магнитной индукции,
|
|
|
и, следовательно, разные значения напряженностей
В этом случае, применяя закон полного тока (3.2), контур интегрирования разбивается по средней линии магнитопровода на «n» участков различного сечения и разного материала. Интеграл заменяется системой «n» слагаемых:
Произведение 
при отсутствии обмотки с током на k-м участке носит название разности скалярных магнитных потенциалов или падения магнитного напряжения вдоль k-го участка
С учетом (3.7) уравнение (3.6) принимает вид:
т.е. сумма магнитных напряжений в контуре равна магнитодвижущей силе.
Это – аналог второго закона Кирхгофа для контура в электрической цепи.
Выразим падение магнитного напряжения на участке через магнитный поток:
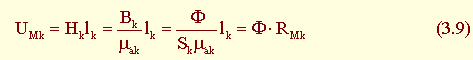
где Sk – сечение магнитопровода на k-м участке;
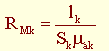(1/Гн) – магнитное сопротивление участка «k» - аналог электрического сопротивления 
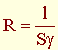проводника длиной l с поперечным сечением S и удельной проводимостью γ.
Таким образом, выражение (3.9) представляет собой закон Ома для участка магнитной цепи. В силу нелинейной зависимости В(Н) ферромагнитного материала магнитное сопротивление RM нелинейно зависит от потока.
Для воздушных зазоров и вставок из диамагнитных материалов магнитная проницаемость принимается равной магнитной постоянной μ0, связь между В и Н принимает вид:
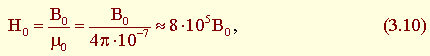
и магнитное сопротивление 
– постоянно.
Из принципа непрерывности магнитного поля (линии магнитной индукции непрерывны и замкнуты) следует, что поток вектора магнитной индукции сквозь замкнутую поверхность равен нулю:
Отсюда следует, что в разветвленной магнитной цепи магнитный поток, подходящий к месту разветвления, равен сумме потоков, отходящих от места разветвления. В этом случае магнитный поток Ф, подобно току в электрической цепи, подчиняется первому закону Кирхгофа:
т.е. алгебраическая сумма магнитных потоков в узле равна нулю.
|
|
|
Итак, к расчету магнитных цепей применимы первый и второй законы Кирхгофа (3.12), (3.8), для линейной магнитной цепи – также и закон Ома (3.10). Так как в основном магнитные цепи нелинейны, к их расчету применимы известные графические и графоаналитические методы расчета нелинейных электрических цепей постоянного тока с построением веберамперных характеристик участков цепи Ф = f(UМ), подобных вольтамперным характеристикам для электрических цепей.
|
|
|
