 |
Входное сопротивление линии
|
|
|
|
Входное сопротивление есть отношение комплексного напряжения к комплексному току в начале линии:
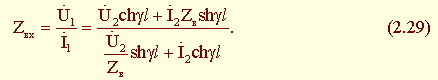
При заданной нагрузке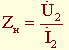 
в конце линии
Формула (2.30) после замены гиперболических функций показательными
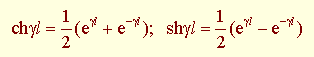
приводится к виду
где ρ – коэффициент отражения на нагрузке (2.27).
В режимах холостого хода (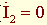
) и короткого замыкания (
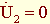) входные сопротивления соответственно (2.29) определяются выражениями:
из которых можно выразить
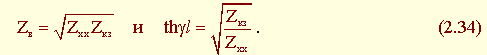
Так, практически путем измерения входных сопротивлений разомкнутой и короткозамкнутой на конце линии определяют ее волновые параметры.
Режим согласованной нагрузки
Режим, когда сопротивление нагрузки равно волновому сопротивлению, называют режимом согласованной нагрузки. В этом случае коэффициент отражения на конце линии (2.27) ρ = 0 и, значит, в линии отсутствуют отраженные волны напряжения и тока.
Входное сопротивление линии (2.31)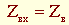 
.
По линии распространяются только прямые волны. Расчетные уравнения принимают вид:
- от начала линии
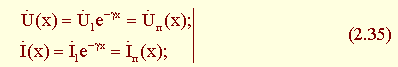
- от конца линии
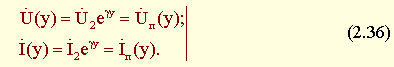
Графики распределения напряжения и тока вдоль линии в режиме согласованной нагрузки показаны на рис. 2.8.
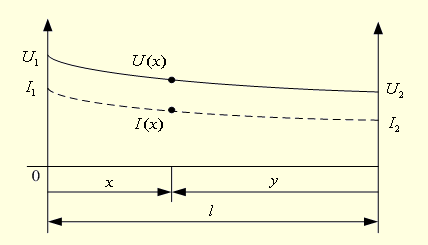
Рис. 2.8. График распределения напряжения и тока вдоль линии в режиме согласованной нагрузки
Режим согласованной нагрузки является самым экономичным. Вся энергия, приносимая прямой электромагнитной волной, поглощается нагрузкой, отсутствует отраженный поток энергии, имеющий место при произвольной нагрузке.
Коэффициент полезного действия (КПД) линии в режиме согласованной нагрузки:
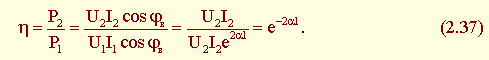
Отсюда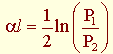 
носит название собственного затухания линии.
Линия без искажений
Линией без искажений называют линию, вдоль которой волны всех частот распространяются с одинаковой фазовой скоростью и с одинаковым коэффициентом затухания.
|
|
|
Сигналы, передаваемые по линиям связи, представляют собой совокупность множества различных частот. Зависимость коэффициентов α и β от частоты (рис. 2.4, 2.5) приводит к амплитудно-фазовым искажениям сигнала, т.к. составляющие разных частот затухают неодинаково и фазовая скорость этих составляющих различна. Сигнал в конце линии получается искаженным, отличающимся по форме от входного сигнала.
Для того, чтобы линия не вносила искажений, коэффициент затухания α и фазовая скорость не должны зависеть от частоты.
Такое условие выполняется при соотношении первичных параметров:
где а – коэффициент пропорциональности.
В этом случае 
.
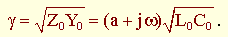Следовательно, параметры неискажающей линии:
Из соотношейний (2.39) видно, что коэффициент α и фазовая скорость Vф не зависят от частоты, а фазовый коэффициент β – зависит от частоты линейно. На рис. 2.5 линейная зависимость β(ω) показана пунктирной линией.
В линии без искажений волновое сопротивление
является активным сопротивлением и тоже не зависит от частоты.
Неискажающая линия согласно (2.39) является еще и линией наименьшего затухания 
(рис. 2.4).
Линия без потерь
На высоких частотах передаваемого сигнала выполняются условия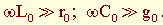 
. Обычно такие линии имеют малую протяженность и для упрощения расчетов принимают r0 = 0; g0 = 0. Фактически потери энергии имеют место, но они незначительны. Такую линию называют линией без потерь.
Вторичные параметры линии без потерь:
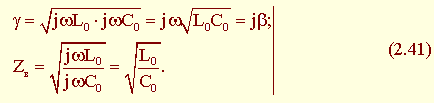
Следовательно, в линии без потерь затухание отсутствует α = 0; коэффициент фазы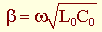 
линейно зависит от частоты, а, значит, фазовая скорость не зависит от частоты:
Волновое сопротивление является чисто активным. Из сравнения выражений (2.39) и (2.41) очевидно, что линия без потерь является также неискажающей линией.
|
|
|
В расчетных уравнениях (2.28) гиперболические функции от мнимого аргумента преобразуются в тригонометрические функции:
и расчетные уравнения для линии без потерь принимают вид:
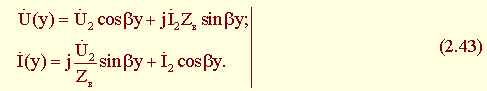
Входное сопротивление линии без потерь при произвольной нагрузке:
|
|
|
