Вычисление площадей плоских фигур и объемов тел вращения с помощью определенного интеграла.

2. Если на отрезке [a; b] функция , то площадь криволинейной трапеции, ограниченной сверху кривой , снизу осью 0X, справа и слева прямыми и (рисунок 1), вычисляется по формуле:

(4.1)

 

 

 

2. Если на отрезке [a; b], то площадь фигуры (рисунок 2) вычисляется по формуле:

(4.2)

3. Если функция меняет знак на отрезке [a; b], то площадь фигуры (рисунок 3) вычисляется по формуле:

, (4.3)

где интегралы по отрезкам, на которых функция отрицательна, берутся по абсолютной величине.

4. Если на одном и том же отрезке [a; b] заданы две функции: и , причем для любых то площадь фигуры (рисунок 4) вычисляется по формуле:

(4.4)

5. Если фигура ограничена сверху разными линиями, заданными на разных отрезках (рисунок 5), имеющих один общий конец: при и при , то площадь такой фигуры определяется по формуле:

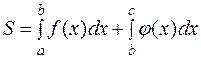(4.5)

Задание 6. Вычислить площадь фигуры ограниченной графиками функций и

Решение

Изобразим фигуру, площадь которой надо найти, на координатной плоскости. Графиком функции g(x) является парабола, ветви которой направлены вверх. Найдем производную функции . Находим координаты вершины параболы С:

Точки пересечения параболы с осями координат:

С осью ох:

;

;

C осью о у: х=0;

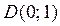
Графиком функции является прямая, которую можно построить по двум точкам с координатами

 

Рисунок 2 к задаче №6

Найдем точки пересечения графиков функций

;

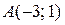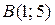
Площадь S фигуры ABC, ограниченной графиками функций, находим по формуле .

Где для всех

Так как 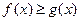при , то

Ответ

 

6. Объем тела, образованного вращением вокруг оси ox криволинейной трапеции, ограниченной непрерывной кривой и прямыми (рисунок 6), равен

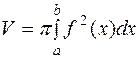(4.6)

 

Рисунок 6

b

0

y

y=f(x)

a

x

 

7. Объем тела, образованного вращением вокруг оси oy криволинейной трапеции, ограниченной непрерывной кривой и прямыми (рисунок 7), равен

(4.7)

 

Несобственные интегралы.

Если функция f(x) непрерывна при , то несобственным интегралам называется . Если этот предел существует и конечен, то интеграл называется сходящимся. В противном случае интеграл называется расходящимся.

Аналогично определяются интегралы

Если функция f(x) непрерывна при и имеет разрыв II рода в точке c, то несобственным интегралом называется

Так же, как и выше, несобственный интеграл называется сходящимся, если оба предела существуют и конечны. В противном случае несобственный интеграл называется расходящимся.

Если же точка разрыва находится в конце промежутка, то:

в) при c=a

г) при c=b

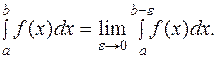
Если при и сходится, то сходится. Такая сходимость называется абсолютной.

Если при и расходится, то расходится.

Если при предел конечен и не равен нулю, то оба интеграла одновременно либо сходятся, либо расходятся.

Аналогичные признаки сходимости можно указать и для несобственных интегралов от разрывных функций.

 

Р Я Д Ы

ВВЕДЕНИЕ

Настоящее пособие является кратким изложением свойств бесконечных рядов, а также представление функций в виде бесконечных рядов более простых функций. Последнее делает бесконечные ряды одним из важнейших численных методов в математике и находит широкое практическое применение.

Рядом в математике называется бесконечная сумма чисел или функций, составленная по определенному закону:

u₁ + u₂ + u₃ + … + u_n +……… (1),

где u_n - члены ряда; многоточие указывает на то, что выражение (1) не имеет последнего слагаемого, т.е. ряд – бесконечная сумма. Поэтому вместо (1), пользуясь знаком суммы, часто пишут так

 

 

Числовые ряды

 

Ряд называется числовым, если члены этого ряда – числа u_n, которые задаются только функциями номера n, т.е. u_n = f(n). Последовательно складывая члены ряда, составим (в бесконечном количестве) суммы:

 

S₁ = u₁ , S₂ = u₁+ u₂ , …, S_n = u₁+ u₂+ u₃+…+ u_n

Их называют частичными суммами ряда.

Конечный или бесконечный предел S частичной суммы S_n ряда (1) при

 

(2)

называют суммой ряда и записывают

S = u₁+ u₂+ u₃+…+ u_n+… =

Если ряд имеет конечную сумму, то его называют сходящимся; в противном случае (т.е. если сумма равна ±¥, либо же суммы вовсе нет) – расходящимся.

Поясним понятие суммы ряда на конкретном примере. Пусть задан числовой ряд

 

(3)

 

каждый последующий член которого равен половине предыдущего.

Подсчитаем суммы одного, двух, трех, четырех, пяти его членов:

S₁ = ,

S₂ = ,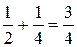

S₃ = ,

S₄ = ,

S₅ = .

Значения этих сумм отличаются от 1 на т.е. при увеличении числа слагаемых получаем для их сумм значения все меньше отличающиеся от 1. Поясним сказанное на рис. 1.

 

 

Рис. 1

 

Прямоугольник площадью в одну квадратную единицу разобьем на два прямоугольника. Один из них вновь разобьем на два прямоугольника одинаковой площади. Продолжая этот процесс деления, получим прямоугольники, площади которых равны квадратных единиц. Объединение этих прямоугольников приближает нас к исходному. Следовательно, и сумма их площадей приближается к площади исходного прямоугольника, т.е. к 1. Число 1 называют суммой ряда (3).

Пример 1.

u_n= 1, S_n = 1 + 1 + 1 + ¼ + 1 = n,

Пример 2.

u_n= (-1) ⁿ, S_n = - 1 + 1 - 1 + 1 – 1 + ¼ + (-1) ⁿ.

 

Такой ряд предела не имеет, т.к. его верхний предел равен 0, а нижний предел равен –1.

Пример 3.

 

u_n= u₁ q^n-1, S_n = u₁ + u₁ q + u₁ q² + ¼ + u₁ q^n-1.

Этот ряд – геометрическая прогрессия со знаменателем q – называется геометрическим рядом. Умножим S_n на q и вычтем полученное выражение почленно из S_n

 

S_n q = u₁ q + u₁ q² + u₁ q³ + ¼ + u₁ qⁿ,

 

S_n - S_n q = u₁ - u₁ qⁿ, S_n (1- q) = u₁ (1- qⁿ).

 

Для частичной суммы S_n геометрического ряда получаем

 

S_n = u₁

 

предел которого и представляет сумму геометрического ряда

 

 

При | q | < 1, 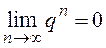и , ряд сходится;

при | q | > 1 ряд геометрической прогрессии расходится;

при q = 1 см. пример 1;

при q = -1 см. пример 2.

Пример 4.

Запишем

 

Представим сумму п членов исследуемого ряда в виде:

тогда 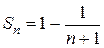и Следовательно, ряд сходится.

 

⇐ Предыдущая9101112131415161718Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: