 |
Пример. Найти неопределенные интегралы
|
|
|
|
а) 
Решение
Преобразуем подынтегральную функцию 
Применим вначале метод замены переменной:
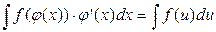 (*)
(*)

 - неправильная рациональная дробь
- неправильная рациональная дробь
Выделим целую часть, для этого выполним следующие преобразования:
 Использовали формулы таблицы интегралов:
Использовали формулы таблицы интегралов:


Ответ: 
4. Интегрирование по частям.
Если  и
и  - дифференцируемые функции, то интегрированием по частям называется нахождение интеграла по формуле:
- дифференцируемые функции, то интегрированием по частям называется нахождение интеграла по формуле:

Интегрирование по частям применяется для интегрирования некоторых трансцендентных функций (lnx, arcsinx, arctgx и тд.), а также произведений алгебраических и трансцендентных функций:
 принимаем за
принимаем за 
 принимаем за
принимаем за 
 принимаем за
принимаем за  ;
;
 принимаем за
принимаем за  ;
;
 принимаем за
принимаем за  ;
;
Аналогичные подстановки и для обратных функций  где
где  - многочлен,,n” степени.
- многочлен,,n” степени.
Пример. 
Решение
Воспользуемся формулой интегрирования по частям:

Примем за 

Найдем дифференциал функции u:

По dv найдем функцию v: 
 (одна из первообразных; постоянную «с» не прибавляем)
(одна из первообразных; постоянную «с» не прибавляем)
Итак, 
Полученный интеграл  найдем, применяя метод замены переменной (формула (*))
найдем, применяя метод замены переменной (формула (*))

Применили формулу таблицы основных интегралов

Итак,

Ответ: 
Иногда, чтобы свести данный интеграл к табличному, приходится применять формулу интегрирования по частям несколько раз.
5. Интегрирование выражений, содержащих квадратный трехчлен в знаменателе.
При интегрировании выражений, содержащих квадратный трехчлен, будем рассматривать такие виды интегралов:
1)  ; 3)
; 3)  ;
;
2)  ; 4)
; 4)  ;
;
где a, b, c, A, B,- действительные числа.
Чтобы найти интеграл вида 1), нужно дополнить квадратный трехчлен до полного квадрата и свести его к табличному вида (18);(19);(20).
 (18)
(18)
 (19)
(19)
 (20)
(20)
Чтобы найти интеграл вида 2), нужно решать по схеме:
|
|
|
а) найти производную квадратного трехчлена и записать ее в числитель;
б) уравнять коэффициенты в числителе;
в) интеграл  разбить на два интеграла и свести к одной из формул вида (18), (19) или (20).
разбить на два интеграла и свести к одной из формул вида (18), (19) или (20).
Интеграл вида 3)  после выделения полного квадрата сводится к табличному интегралу вида(21) или (16).
после выделения полного квадрата сводится к табличному интегралу вида(21) или (16).
Интеграл вида 4)  решается по плану, предложенному для нахождения интегралов вида 2), но интеграл нужно свести к табличному вида (16) или (21).
решается по плану, предложенному для нахождения интегралов вида 2), но интеграл нужно свести к табличному вида (16) или (21).
6. Интегрирование рациональных дробей.
Рациональной дробью называется дробь вида  , где
, где
 и
и  - многочлены.
- многочлены.
Рациональная дробь называется правильной, если показатель степени многочлена  ниже показателя степени многочлена
ниже показателя степени многочлена  , в противном случае дробь называется неправильной.
, в противном случае дробь называется неправильной.
Если дробь неправильная, то делением числителя на знаменатель по правилу деления многочлена на многочлен выделяют “целую” часть и представляют дробь в виде суммы многочлена и правильной дроби. Затем правильную дробь разлагают в сумму элементарных дробей.
Простейшими (элементарными) дробями называются дроби следующего вида:
1.  2.
2.  где
где 
3.  , где
, где 
т.е. квадратный трехчлен  не имеет действительных корней.
не имеет действительных корней.
Рассмотрим интегралы от простейших дробей:
1. 
2. 
3. 
т.е. нахождение интеграла (3) уже известно, так как  , то он сводится к табличному интегралу (18).
, то он сводится к табличному интегралу (18).
Приведенные формулы для интегрирования простейших дробей запоминать не обязательно. В каждом конкретном примере эти интегралы следует находить изученными ранее методами.
Для разложения правильной рациональной дроби на элементарные, необходимо сначала разложить знаменатель на линейные и квадратные множители:
 ,
, 
Затем записать схему разложения данной дроби на элементарные в следующем виде;

где  - некоторые постоянные.
- некоторые постоянные.
В этом разложении следует обратить внимание на следующее:
- если в знаменателе линейный множитель или его степень, то в числителе постоянное число;
|
|
|
- если в знаменателе квадратный трехчлен (с комплексными корнями) или его степень, то в числителе многочлен первой степени.
Постоянные коэффициенты правой части разложения (*) находятся методом неопределенных коэффициентов двумя способами:
I способ.
1. Приведением дробей правой части к общему знаменателю получаем равенство двух дробей с одинаковыми знаменателями;
2. Приравнивая числители дробей, получаем тождественно равные многочлены.
3. Используя теорему о тождественно равных многочленах, сравниваем коэффициенты при одинаковых степенях в обоих частях полученного тождества. Это приводит к системе, из которой находятся искомые коэффициенты. Этот способ называется способом сравнения.
Подставив найденные коэффициенты в разложение дроби  , сводим интегрирование этой дроби к интегрированию известных простейших дробей.
, сводим интегрирование этой дроби к интегрированию известных простейших дробей.
Проще при этом вычисляются коэффициенты, если в качестве числовых значений брать действительные корни знаменателя.
II способ - способ частных значений.
Можно определить коэффициенты, если в полученном тождестве переменной x придать произвольные значения или корни знаменателя, если они есть. Часто бывает полезно комбинировать оба способа.
Определенный интеграл
Пусть функция  определена и ограничена на отрезке [a, b] и
определена и ограничена на отрезке [a, b] и  - произвольное разбиение этого отрезка на n элементарных промежутков. Предположим, что на каждом отрезке
- произвольное разбиение этого отрезка на n элементарных промежутков. Предположим, что на каждом отрезке  выбрана точка
выбрана точка  . Тогда сумма
. Тогда сумма  называется интегральной суммой функции
называется интегральной суммой функции  на отрезке [a, b], а её предел при
на отрезке [a, b], а её предел при  , если он существует и конечен, называется определенным интегралом от функции
, если он существует и конечен, называется определенным интегралом от функции  в пределах от a до b и обозначается так:
в пределах от a до b и обозначается так:

Определенный интеграл не должен зависеть от разбиений и выбора точек  .
.
Если определенный интеграл существует, то функция  называется интегрируемой на отрезке [a; b].
называется интегрируемой на отрезке [a; b].
Если функция  непрерывна на отрезке [a; b], то существует первообразная от этой функции на отрезке [a; b].
непрерывна на отрезке [a; b], то существует первообразная от этой функции на отрезке [a; b].
|
|
|


