 |
Если для ряда (1) с положительными членами
|
|
|
|
(6)
то: а) при l < 1 ряд сходится; б) при l > 1 ряд расходится; в) при l = 1 признак ответа не дает.
Д о к а з а т е л ь с т в о проведем для l < 1 (случай l > 1 доказывается аналогично). Возьмем число q такое, что l< q < 1, тогда, начиная с некоторого номера n ³ N выполнено неравенство 
или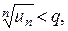 
откуда un < qn для всех n³ N. Отбросим первые N -1 членов в ряде (1), тогда получим ряд
uN+ uN +1 + uN +2 +…, (7)
все члены которого меньше соответствующих членов ряда:
qN + qN +1 + qN +2 + ¼ (8)
Этот ряд при q < 1 - убывающая геометрическая прогрессия. Члены ряда (7), начиная с номера n ³ N, меньше членов ряда (8). Из сходимости ряда (8) следует сходимость ряда (7).
Интегральный признак
Пусть члены ряда (1) положительны и не возрастают, т.е. u 1 ³ ³ u 2 ³ u 3 ³ ¼ и пусть f (x) такая непрерывная и невозрастающая функция, что f (1) = u 1, f (2) = u 2, ¼, f (n) = un, ¼, тогда справедливы следующие утверждения.
1) Если несобственный интеграл 
сходится, то сходится и ряд (1).
2) Если указанный интеграл расходится, то расходится и ряд (1).
На координатной плоскости отметим по оси x значения x =1,2,3,¼, которые соответствуют n =1,2,3,¼, и в каждой точке x =1,2,3,¼ восстановим перпендикуляр, длиной равной un. Соединим
все точки плавной линией (см. рис. 2).
y
y = f(x)
u1 u2 u3 u4
0 1 2 3 4 n n+1 x
Рис. 2
Сумма площадей прямоугольников, построенных таким образом, что основание равно 1, а высота un, начиная с n = 1
Sn= u 1 + u 2 + u3+ …+ un >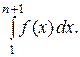 
На рис. 3 сумма площадей всех построенных прямоугольников равна сумме всех членов ряда, начиная со второго до (n +1)-го, т.е.
Sn+ 1 - u 1 < 
y
y =f(x)
u1 u2 u3 u4
0 1 2 3 4 n n + 1 x
Рис. 3
или
Sn+ 1 < + u 1.
Пусть сходится, т.е. < 
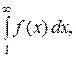и Sn < Sn+ 1 < < + u 1. Это означает, что частичные суммы ограничены при всех n и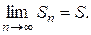 
Ряд сходится.
|
|
|
Пример 6. Установить сходимость ряда с общим членом un = =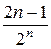 
. Запишем (n +1)-ый член ряда
un +1 =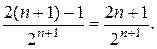 
Согласно признаку Даламбера
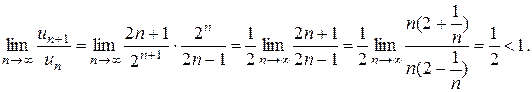
Ряд сходится.
Пример 7. Установить сходимость ряда с общим членом un = =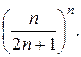 
Посчитаем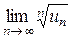 
Ряд сходится по признаку Коши.
Пример 8. Установить сходимость гармонического ряда un =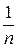 
. Воспользуемся интегральным признаком сходимости, тогда f (x) = 
.
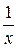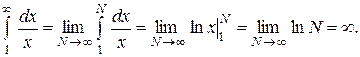
Несобственный интеграл расходится, а, следовательно, расходится и гармонический ряд.
Знакопеременные ряды
Знакопеременными называются ряды, члены которых поочередно имеют то положительный, то отрицательный знаки.
Знакопеременный ряд удобнее записывать так, чтобы знаки членов были выявлены (при этом считаем все un > 0):
u 1 - u 2 + u 3- u 4 + …+ (-1) n- 1 un + ¼ (9)
По отношению к подобным рядам Лейбниц доказал следующую простую теорему.
Теорема Лейбница. Если члены знакопеременного ряда (9) монотонно убывают по абсолютной величине, т.е. un +1 < un (n = 1,2,3,¼), и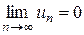 
, то ряд сходится, его сумма положительна и не превосходит первого члена.
Д о к а з а т е л ь с т в о. Частичную сумму четного порядка можно записать в виде
S2m = (u 1- u 2) + (u 3- u 4) + …+ (u 2 m- 1 - u 2 m ).
Из условия теоремы следует, что выражения в каждой скобке положительны. Следовательно, частичная сумма четного порядка S2m > 0 и возрастает с возрастанием m. С другой стороны, если записать эту же сумму так:
S2m = u 1 - (u 2 - u 3) - (u 4- u 5) - …- (u 2 m- 2 - u 2 m -1) - u 2 m ,
то каждая из скобок оказывается положительной, т.е. S2m < u 1, а значит,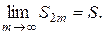 
Частичная сумма нечетного порядка S2m+ 1 = S2m + u 2 m +1. По условию теоремы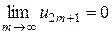 
, а, согласно доказанному, 
, тогда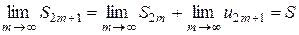 
. Теорема доказана.
Пример 9. Установить сходимость ряда
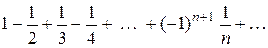
В этом ряде 1 > 
> 
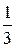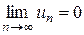> ¼, . Согласно теореме Лейбница, ряд сходится.
Замечание. Погрешность | S-Sn | ряда (9) не превосходит модуля первого отброшенного слагаемого, т.е. | S-Sn | £ | un +1|. Так, в примере 9, погрешность приближения | S-Sn | £ 
.
|
|
|
Рассмотрим знакопеременный ряд (9) и ряд, составленный из модулей его членов
| u 1| + | u 2| + | u 3| + ¼ + | un |+ ¼ (10)
Если ряд (10) сходится, то и данный знакопеременный ряд (9) также сходится (по свойству 3).
Рассмотренный в примере 9 ряд сходится условно, т.к., согласно доказанному в примере 8, соответствующий гармонический ряд расходится.
Степенные ряды
Ряд (1) называют функциональным, если его члены являются функциями от x.
Простейшим функциональным рядом является степенной ряд
a 0 + a 1 x + a 2 x 2 + ¼ + an xn + ¼, (11)
или в более общем виде:
a 0 + a 1(x - x 0 ) + a 2 (x - x 0 )2 + ¼ + an (x - x 0 ) n + ¼ (12)
Ряд (12) не отличается существенно от ряда (11), так как может быть сведен к нему заменой переменной: x - x 0 = y.
Давая x определенные числовые значения, получаем различные числовые ряды, которые могут оказаться сходящимися или расходящимися.
Совокупность значений x, при которых функциональный ряд сходится, называют областью сходимости этого ряда. В области сходимости ряда его сумма является функцией от x и обозначается через S (x).
Можно доказать, что для любого степенного ряда (11) существует конечное или бесконечное число R > 0, такое, что при | x | < R ряд сходится, а при | x | > R ряд расходится. При | x | = R, т.е. при x = R и x = - R, ряд может сходится или расходится. Число R называют радиусом сходимости, а интервал (- R, R) - интервалом сходимости. Для ряда (12) интервал сходимости | x - x 0 | < R или x 0 - R < x < x 0 + R.
Для определения области сходимости степенных рядов можно применить признак Даламбера. Рассмотрим соответствующий степенному ряду (11) ряд, составленный из модулей его членов:
| a 0 | + | a 1 | | x | + | a 2 | | x | 2 + ¼ + | an | | x |n + ¼ (13)
Если ряд (13) сходится, то сходится и ряд (11).
Согласно признаку Даламбера для сходимости ряда (13) должно выполнятся условие:
,
или | x | < 
,
т.е. радиус сходимости определяется через коэффициенты степенного ряда: R = .
Аналогичным образом для определения радиуса сходимости можно воспользоваться и признаком Коши, тогда
.
Отсюда, | x | <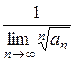 
, или R = .
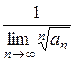Как указывалось выше, сумма степенного ряда представляет собой функцию, определенную в интервале сходимости (- R, R) этого ряда. Можно доказать, что функция
|
|
|
= a 0 + a 1 x + a 2 x 2 + ¼ + an xn + ¼ (11¢)
дифференцируема и ее производная 
может быть найдена почленным дифференцированием ряда (11¢):
= a 1 + 2 a 2 x + ¼ + n an xn -1 + ¼
при - R < x < R. То же справедливо и для производных второго, третьего и т.д. порядков.
Аналогично, неопределенный интеграл от функции f (x) для всех x из области сходимости может быть получен почленным интегрированием ряда (11¢):
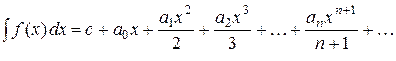
Степенной ряд в области сходимости по отношению к операциям дифференцирования и интегрирования ведет себя как многочлен, что делает степенные ряды удобным средством для приближенных вычислений.
|
|
|
