Требования к технике безопасности при выполнении

Практических работ

- Вход в аудиторию осуществляется только по разрешению преподавателя.

- На первом занятии преподаватель проводит первичный инструктаж по технике безопасности и напоминает студентам о бережном отношении к оборудованию и о материальной ответственности каждого из них за сохранность оборудования и обстановки.

- При обнаружении повреждений оборудования персональную ответственность несут студенты, выполнявшие работу на этом оборудовании. Виновники обязаны возместить материальный ущерб.

- Если во время проведения работы на оборудовании замечены какие-либо неисправности оборудования, необходимо немедленно сообщить об этом преподавателю.

- После окончания работы рабочее место следует привести в порядок.

 

Практическая работа № 1

Тема Решение систем линейных уравнений различными методами

Цель работы:       

Используя теоретический материал и образцы решения, закрепить навыки решения задач по теме «Решение систем линейных алгебраических уравнений различными способами»

 

В результате выполнения работы студенты осваивают следующие результаты обучения в соответствии с ФГОС СПО:

умения:

- решать прикладные задачи в области профессиональной деятельности;

знания:

-значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;

-основные понятия и методы математического анализа, линейной алгебры, теории комплексных чисел, теории вероятностей и математической статистики;

Порядок выполнения работы:

1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.

2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.

3. Сделайте выводы по результатам работы

Теоретическая часть

1. Пусть дана система линейных уравнений

     (1)

Коэффициенты a₁₁,₁₂,..., a_1n,..., a_n1 , b₂,..., b_n считаются заданными.

Вектор -строка íx₁, x₂,..., x_n ý - называется решением системы (1), если при подстановке этих чисел вместо переменных все уравнения системы (1) обращаются в верное равенство.

  Определитель n-го порядка D=çAê=ça _ij ç, составленный из коэффициентов при неизвестных, называется определителем системы (1). В зависимости от определителя системы (1) различают следующие случаи:

    a) Если D¹, то система (1) имеет единственное решение, которое может быть найдено по формулам Крамера: x₁= 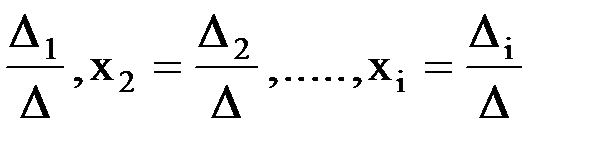, где

определитель n-го порядка D_i (i=1,2,...,n) получается из определителя системы путем замены i-го столбца свободными членами b₁ , b₂ ,..., b_n.

    б) Если D=, то система (1) либо имеет бесконечное множество решений, либо несовместна,т.е. решений нет.

 

2. Рекомендации по выполнению заданий

1. Рассмотрим систему 3-х линейных уравнений с тремя неизвестными.

    (2).

 1. В данной системе составим определитель   и вычислим.

 

  2. Составить и вычислить следующие определители:

 .

3. Воспользоваться формулами Крамера.

 

Практическое значение правила Крамера для решения системы n линейных уравнений с п неизвестными невелико, так как при его применении приходится вычислять п +1 определителей n -го порядка: D, D _{x 1}, D _{x 2}, …, D x_n. Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

 

        

 

Более удобным является так называемый метод Гаусса. Он применим и в более общем случае системы линейных уравнений, т. е. когда число уравнений не совпадает с числом неизвестных.

    Итак, пусть дана система, содержащая m линейных уравнений с п неизвестными:

                               а₁₁х₁ + а₁₂х₂ + …+ а_{1 n} х_n = b₁;

                               а₂₁х₁ + а₂₂х₂ + …+ а_{2 n} х_n = b₂;                    

_.                                    ……………………………………

                              а_m1х₁ + а_m2х₂ + …+ а_{m n} х_n = b_m

    Метод Гаусса решения системы заключается в последовательном исключении переменных.

Предыдущая1234567Следующая

Поделиться:

Воспользуйтесь поиском по сайту: