 |
Основные теоремы теории вероятностей.
|
|
|
|
Теорема сложения вероятностей несовместных событий. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий, то есть
Р(А+В)= Р(А)+Р(В)
Следствие. Пусть события 
и 
– противоположны. Сумма вероятностей противоположных событий равна единице, то есть
.
Теорема сложения вероятностей совместных событий: Вероятность суммы двух совместных событий равна сумме вероятностей событий без вероятности их совместного появления, то есть
Р(А+В)= Р(А)+Р(В) - Р(АВ)
Теорема умножения вероятностей: Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого (условной вероятностью события A при условии В называется вероятность события А найденная при условии, что событие В произошло, обозначается Р(А|В))
Р(АВ)= Р(В) Р(А|В)= Р(А)Р(В|А)
Определение: События А и В называются независимыми если наступление одного из них не оказывает влияния на вероятность другого.
Теорема умножения вероятностей независимых событий: Вероятность произведения двух независимых событий А и В равна произведению вероятностей этих событий.
Р(АВ)= Р(А)Р(В).
Случайная величина – величина, численное значение которой может меняться в зависимости от результата стохастического эксперимента.
Дискретной назовём случайную величину, возможные значения которой образуют конечное множество.
Законом распределения дискретной случайной величины называется правило, по которому каждому возможному значению xi ставится в соответствие вероятность pi, с которой случайная величина может принять это значение, причём 
.
|
|
|
Определение: Математическим ожиданием случайной величины называется число, равное сумме произведений всех значений случайной величины на вероятности этих значений.
Математическое ожидание случайной величины X обозначается через MX. Если случайная величина X принимает значения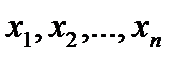 
соответственно с вероятностями 
, то согласно определению:
. (1)
Математическое ожидание часто называют средним значением случайной величины, так как оно указывает некоторое «среднее число», около которого группируются все значения случайной величины.
Определение: Пусть задан закон распределения случайной величины X:
| 0 | 1 | … | k | … | n |
| 
| 
| … | 
| … | 
|
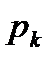
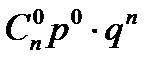
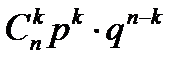
Тогда такое распределение называется распределением Я. Бернулли или биноминальным распределением, причём верно равенство
. (2)
Определение: Дисперсией случайной величины называется математическое ожидание квадрата отклонения случайной величины от её математического ожидания.
Дисперсия случайной величины X обозначается через DX. Следовательно,
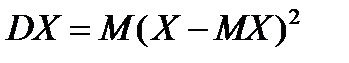. (4)
Пусть случайная величина X принимает значения 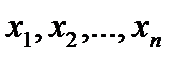соответственно с вероятностями . Тогда квадрат отклонения случайной величины X от её математического ожидания есть случайная величина, которая принимает значения
, 
, …, 
, …, 
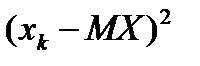соответственно с вероятностями 
.
Поэтому математическое ожидание так распределённой случайной величины, то есть дисперсию X, можно записать в виде:
. (5)
Дисперсия случайной величины характеризует степень разброса, рассеивание случайной величины относительно её математического ожидания (среднего значения).
|
|
|
Теорема 2. Дисперсия случайной величины равна математическому ожиданию квадрата этой величины без квадрата её математического ожидания, то есть
. (6)
Вариант№0
Задание 1. В группе 30 студентов. Необходимо выбрать старосту, заместителя старосты и профорга. Сколько существует способов это сделать?
Решение. Старостой может быть выбран любой из 30 студентов, заместителем - любой из оставшихся 29, а профоргом – любой из оставшихся 28 студентов, т.е. n1=30, n2=29, n3=28. По правилу умножения общее число N способов выбора старосты, его заместителя и профорга равно N=n1´n2´n3=30´29´28=24360.
Задание 2. В шахматном турнире участвуют 16 человек. Сколько партий должно быть сыграно в турнире, если между любыми двумя участниками должна быть сыграна одна партия?
Решение. Каждая партия играется двумя участниками из 16 и отличается от других только составом пар участников, т.е. представляет собой сочетания из 16 элементов по 2. Их число равно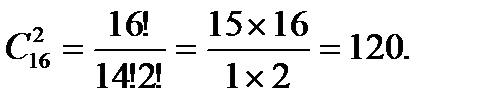 
Задание 3. В ящике 5 апельсинов и 4 яблока. Наудачу выбираются 3 фрукта. Какова вероятность, что все три фрукта – апельсины?
Решение. Элементарными исходами здесь являются наборы, включающие 3 фрукта. Поскольку порядок фруктов безразличен, будем считать их выбор неупорядоченным (и бесповторным). Общее число элементарных исходов 
равно числу способов выбрать 3 фрукта из 9, т.е. числу сочетаний 
. Число благоприятствующих исходов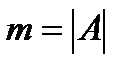 
равно числу способов выбора 3 апельсинов из имеющихся 5, т.е. 
. Тогда искомая вероятность
.
Задание 4. В ящике 10 красных и 5 синих пуговиц. Вынимаются наудачу две пуговицы. Какова вероятность, что пуговицы будут одноцветными?
Решение.
Событие A={вынуты пуговицы одного цвета} можно представить в виде суммы 
, где события 
и 
означают выбор пуговиц красного и синего цвета соответственно. Вероятность вытащить две красные пуговицы равна 
, а вероятность вытащить две синие пуговицы 
. Так как события и 
не могут произойти одновременно, то в силу теоремы сложения
Задание 5. Монета подбрасывается 3 раза. Найти наиболее вероятное число успехов (выпадений герба).
Решение.
Возможными значениями для числа успехов в трех рассматриваемых испытаниях являются m = 0, 1, 2 или 3. Пусть Am - событие, состоящее в том, что при трех подбрасываниях монеты герб появляется m раз. По формуле Бернулли легко найти вероятности событий Am
|
|
|
| m | 0 | 1 | 2 | 3 |
| Pn(m) | 1/8 | 3/8 | 3/8 | 1/8 |
Из этой таблицы видно, что наиболее вероятными значениями являются числа 1 и 2 (их вероятности равны 3/8). Этот же результат можно получить и из теоремы 2. Действительно, n=3, p=1/2, q=1/2. Тогда
, т.е. 
.
|
|
|
