 |
Требования к содержанию отчета по работе
|
|
|
|
Отчёт о работе должен содержать название и цель работы, задание, результаты выполнения задания. По результатам работы необходимо сделать выводы.
Контрольные вопросы (Задания для самопроверки качества освоенных результатов обучения):
- определение вероятности события
- теорема сложения вероятностей
- теорема умножения вероятностей
- понятие случайной величины
- законом распределения случайной величины
- формула математического ожидания и дисперсии случайной величины
Приложение
Задание 1. Задает ли закон распределения дискретной случайной величины данная таблица
1)
| X | 2 | 3 | 4 | 5 | 6 |
| P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
2)
| X | 21 | 22 | 23 | 24 | 25 |
| P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
3)
| X | 4 | 5 | 6 | 7 | 8 |
| P | 0,13 | 0,17 | 0,3 | 0,37 | 0,68 |
4)
| X | 9 | 10 | 11 | 12 | 13 |
| P | 0,2 | 0,3 | 0,11 | 0,13 | 0,47 |
5)
| X | 2 | 3 | 4 | 5 | 6 |
| P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
6)
| X | 21 | 22 | 23 | 24 | 25 |
| P | 0,11 | 0,19 | 0,2 | 0,2 | 0,3 |
7)
| X | 4 | 5 | 6 | 7 | 8 |
| P | 0,13 | 0,17 | 0,3 | 0,37 | 0,68 |
8)
| X | 9 | 10 | 11 | 12 | 13 |
| P | 0,2 | 0,3 | 0,11 | 0,13 | 0,47 |
9)
| X | 2 | 3 | 4 | 5 | 6 |
| P | 0,1 | 0,2 | 0,25 | 0,17 | 0,3 |
Задание 2. Дискретная случайная величина имеет закон распределения. Найти неизвестную вероятность.
1)
| X | 5 | 6 | 7 | 8 | 9 |
| P | 0,13 | 0,3 | 0,2 | P4 | 0,17 |
2)
| X | 4 | 5 | 6 | 7 | 8 |
| P | 0,15 | 0,16 | P3 | 0,5 | 0,07 |
3)
| X | 1 | 2 | 3 | 4 | 5 |
| P | 0,3 | P2 | 0,2 | 0,29 | 0,1 |
4)
| X | 1 | 2 | 3 | 4 | 5 |
| P | 0,16 | P2 | 0,15 | 0,07 | 0,5 |
5)
| X | 5 | 6 | 7 | 8 | 9 |
| P | 0,13 | 0,3 | 0,2 | P4 | 0,17 |
6)
| X | 4 | 5 | 6 | 7 | 8 |
| P | 0,15 | 0,16 | P3 | 0,5 | 0,07 |
8)
| X | 1 | 2 | 3 | 4 | 5 |
| P | 0,3 | P2 | 0,2 | 0,29 | 0,1 |
9)
| X | 5 | 6 | 7 | 8 | 9 |
| P | 0,13 | 0,3 | 0,2 | P4 | 0,17 |
Задание 3.
| №1. Из 40 вопросов, входящих в экзаменационные билеты, студент знает 30. Найти вероятность того, что среди трех наугад выбранных вопросов студент знает 2 вопроса. |
| №2. В лотерее разыгрывается 100 билетов. Выигрыши выпали на 20 билетов. Некто приобрел 5 билетов. Найти вероятность того, что выигрыш выпадет хотя бы на один билет. |
| №3.Какова вероятность того, что два определенных студента будут посланы на практику в город С, если в наличии имеется 5 мест в город А, 8- в город В и 7 – в город С. |
| №4. Один студент выучил 20 из 25 вопросов программы по математике, а второй - только 15. каждому из них задают по одному вопросу. Найти вероятность того, что правильно ответит только первый студент. |
| №5. Из букв А, А, И, Л, М, Н разрезной азбуки выбирают наудачу по одной и ставят в ряд. Найти вероятность того, что получится слово: МИНА. |
| №6. В ящике содержаться 9 белых, 6 черных и 5 зеленых шаров. Наудачу вынимается один шар. Найти вероятность того, что он окажется либо черным, либо зеленым. |
| №7. В ящике находится 20 деталей, 4 из них – нестандартные. Какова вероятность того, что среди 6 наугад взятых деталей нестандартных не окажется? |
| №8. В группе 10 юношей и 10 девушек. Для дежурства путем жеребьевки выделяют 5 человек. Какова вероятность того, что в число дежурных войдут 2 юношей и 3 девушки? |
| №9. Три стрелка делают по одному выстрелу в цель. Вероятности попаданий в цель соответственно равны 0,6; 0,85; 0,7. Какова вероятность попадания в цель только второго стрелка? |
Задание 4.
|
|
|
Вариант1
1. Случайная величина X распределена по закону:
| –1 | 0 | 1 | 2 |

| 
| 
| 
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. В лотерее разыгрывается 20000 билетов. Найдите математическое ожидание и дисперсию числа выигрышных билетов, если каждый билет может выигрышным с вероятностью 0,3.
Вариант 2
1. Случайная величина X распределена по закону:
| 0 | 1 | 2 | 3 |

| 
| 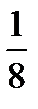
| 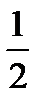
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. В магазин поступила партия из 50 коробок с обувью черного и коричневого цвета. Найдите математическое ожидание и дисперсию числа коробок с обувью коричневого цвета, если вероятность того, что обувь будет коричневого цвета равна 0,2.
|
|
|
Вариант 3
1. Случайная величина X распределена по закону:
| –1 | 0 | 1 |
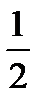
| 
| 
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа не взошедших семян из 800 посеянных семян данного растения, если каждое из семян может не взойти с вероятностью 0,01.
Вариант 4
1. Случайная величина X распределена по закону:
| –1 | 1 | 2 | 3 |
| 0,1 | 0,2 | 0,3 | 0,4 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа студентов, которые не сдадут экзамен, в группе из 30 человек, если каждый студент может не сдать экзамен с вероятностью 0,4.
Вариант 5
1. Случайная величина X распределена по закону:
| –2 | –1 | 1 | 2 |
| 0,2 | 0,1 | 0,2 | 0,5 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. В урне находятся всего 100 белых и чёрных шаров. Найдите математическое ожидание и дисперсию числа белых шаров, если вероятность того, что шар будет белым равна 0,02.
Вариант 6
1. Случайная величина X распределена по закону:
| 1 | 2 | 3 |
| 0,07 | 0,03 | 0,9 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа нестандартных ламп в партии из 300 ламп, если каждая лампа может оказаться нестандартной с вероятностью 0,07.
Вариант 7
1. Случайная величина X распределена по закону:
| –1 | 1 | 2 |

| 
| 
|
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа фальшивых билетов, купленных на самолёт, в партии из 150 билетов, если каждый билет может оказаться фальшивым с вероятностью 0,004.
Вариант 8
1. Случайная величина X распределена по закону:
| 0 | 1 | 2 |
| 0,4 | 0,5 | 0,1 |
Найдите математическое ожидание и дисперсию случайной величины X.
2. Найдите математическое ожидание и дисперсию числа изделий со знаком качества в партии из 7000 деталей, если каждая деталь может оказаться со знаком качества с вероятностью 0,8.
Вариант 9
1. Случайная величина X распределена по закону:
| –1 | 0 | 1 |
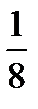
| 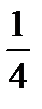
| 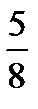
|
Найдите математическое ожидание и дисперсию случайной величины X.
|
|
|
2. Найдите математическое ожидание и дисперсию числа поддельных медицинских препаратов в партии из 126 препаратов, если каждый препарат может быть поддельным с вероятностью 0,06.
Список литературы
Основные источники:
1. Григорьев С.Г., Иволгина С.В. «Математика»: учебник для студ. образоват. учреждений сред.проф. образования под редакцией В.А. Гусева. – 10-е изд., стер. – М.: Издательский центр «Академия», 2014.
Дополнительные источники:
2. Богомолов Н.В., Самойленко П.И. «Математика» учебник для средних спец. учебных заведений -5 изд., переработанное и доп. – М.: издательство Юрайт, 2015.
3. Богомолов Н.В. практические занятия по математике: учебное пособие для СПО / Н.В. Богомолов. – 11-е изд., перераб. И доп. –М.: издательство Юрайт, 2015.
4. Федеральное хранилище Единой коллекции цифровых образовательных ресурсов [Электронный ресурс] / Национальный фонд подготовки кадров – Электрон.дан. – Режим доступа: http://school-collection.edu.ru/catalog/– Загл. с экрана;
5. Единое окно доступа к образовательным ресурсам [Электронный ресурс]: каталог образовательных Интернет - ресурсов/ ФГУ ГНИИ ИТТ «Информика». – Электрон.дан. – Режим доступа: http://window.edu.ru/– Загл. с экрана;
|
|
|


