 |
Задание 1.Решение системы линейных уравнений методом Крамера
|
|
|
|
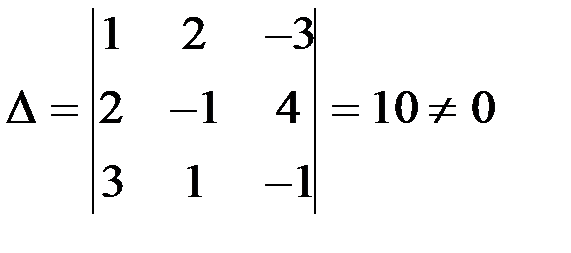
Проверка:
Ответ: x=0,5; y=2; z=1,5.
Задание 2. Решить методом Гаусса систему уравнений
x 1 – 2 x 2 + x 3 + x 4 = –1;
3 x 1 + 2 x 2 – 3 x 3 – 4 x 4 = 2;
2 x 1 – x 2 + 2 x 3 – 3 x 4 = 9;
x 1 + 3 x 2 – 3 x 3 – x 4 = –1.
Решение:Составим матрицу В и преобразуем ее. Для удобства вычислений отделимвертикальной чертой столбец, состоящий из свободных членов:
1 –2 1 1 –1
B = 3 2 –3 –4 2
2 –1 2 –3 9
1 3 –3 –1 –1
Умножим первую строку матрицы В последовательно на 3, 2 и 1 и вычтем соответственно из второй, третьей и четвертой строк. Получим матрицу,эквивалентную исходной:
1 –2 1 1 –1
0 8 –6 –7 5
0 3 0 –5 11
0 5 –4 –2 0
Третью строку матрицы умножим на 3 и вычтем ее из второй строки. Затем новую вторую строку умножим на 3 и на 5 и вычтем из третьей и четвертой строк. Получим матрицу, эквивалентную исходной:
1 –2 1 1 –1
0 –1 –6 8 –28
0 0 –1 0 –3
0 0 0 19 –19
Из коэффициентов последней матрицы составим систему, равносильную исходной:
x 1 – 2 x 2 + x 3 + x 4 = –1;
|
|
|
– X 2 – 6 x 3 + 8 x 4 = –28;
– x 3 = –3;
19 x 4 = –19.
Решим полученную систему методом подстановки, двигаясь последовательно от последнего уравнения к первому. Из четвертого уравнения x 4 = –1, из третьего х 3 = 3. Подставив значения х3 и x 4 во второе уравнение, найдем x2 = 2. Подставив значения x 2, x3, x4 в первое уравнение, найдем x 1 = 1.
Ответ. (1; 2; 3;-1).
Задание 3. Решить систему уравнений методом обратной матрицы.
|
| 2 x1 | + | 3 x2 | = | 4 | |
| - 2 x1 | + | x2 | = | 5 |
Решение:
Введем обозначения:
| A = |
| 2 | 3 |
| - матрица А состоит из коэффициентов системы. |
| -2 | 1 |
| X = |
| x 1 |
| - матрица X состоит из переменных, которые необходимо найти. |
| x 2 |
| B = |
| 4 |
| - матрица B состоит из столбца свободных членов. |
| 5 |
| E = |
| 1 | 0 |
| - единичная матрица. |
| 0 | 1 |
Теперь исходную систему уравнений можно записать в виде матричного уравнения.
A * X = B
Умножим (слева) левую и правую часть уравнения на A-1 - матрицу обратную матрице A.
A -1 * A * X = A -1 * B
Согласно определению обратной матрицы: A -1 * A = E
E * X = A -1 * B
Согласно определению единичной матрицы: E * X = X
X = A -1 * B
задача сводится к нахождению обратной матрицы A -1
| * |
|
| X = A -1 * B = 1 / 8 * |
| -11 |
|
| 18 |
| X = |
| -11/8 |
|
| 9/4 |
Ответ:
x1 = -11/8
x2 = 9/4
Задание 4. Сложить и умножить комплексные числа 
и 
.
Решение. Для сложения чисел производим следующие вычисления:
Теперь умножаем:
Ответ.5+5i, 2+11i
Приложение:
ВАРИАНТ 1
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 2
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
|
|
|
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 3
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 4
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
ВАРИАНТ 5
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 6
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
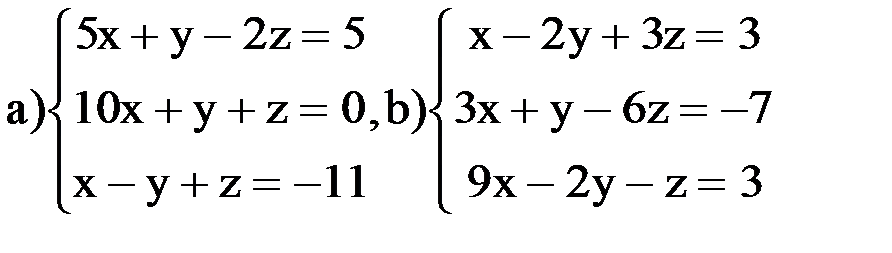
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 7
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 8
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 9
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
ВАРИАНТ 10
Задание 1. Найти решение систем линейных уравнений методами Крамера, Гаусса, обратной матрицы:
Задание 2. Вычислить, выписать вещественную и мнимую части полученных комплексных чисел.
Практическая работа №2. Предел функции. Вычисление производной функции. Исследование и построение графиков функций с помощью производной
Цель работы. Сформировать навыки вычисления пределов последовательностей и пределов функций. Сформировать умение находить производные сложных функций, усвоить геометрический и физический смысл производной. Сформировать навыки нахождения неопределенных интегралов различными методами
|
|
|
В результате выполнения работы студенты осваивают следующие результаты обучения в соответствии с ФГОС СПО:
умения:
- решать прикладные задачи в области профессиональной деятельности;
знания:
-значение математики в профессиональной деятельности и при освоении профессиональной образовательной программы;
-основные математические методы решения прикладных задач в области профессиональной деятельности;
-основные понятия и методы математического анализа
основы интегрального и дифференциального исчисления
Порядок выполнения работы:
1. Повторите теоретические положения по теме и записать определение, формулы расчета и т.п.
2. Выполните задание, согласно своего варианта. Исходные данные возьмите в приложении.
3. Сделайте выводы по результатам работы
Теоретическая часть
Определение: Пусть функция f (x) определена в некоторой окрестности точки а, кроме, быть может, самой точки а. Число А называется пределом функции f (x) в точке а (или при х, стремящемся к а), если для любых значений аргумента (х ¹ а) изсколь угодно малой окрестности точки а, последовательность соответствующих значений функции f (x) мало чемотличается от А (т.е. f (x) приближенно равны А).
В этом случае пишут 
Свойства пределов:
Теорема 1: Функция не может иметь двух разных пределов в точке.
Теорема 2: Предел суммы (разности) функций равен сумме (разности) их пределов, если последние существуют: 
,
Теорема 3: Предел произведения функций равен произведению их пределов, если последние существуют: 
,
Следствие: Постоянный множитель можно выносить за знак предела, т.е.
,
Теорема 4: Предел отношений двух функций равен отношению их пределов, если последние существуют и предел делителя отличен от нуля:
,
Правила дифференцирования
1) 
;
2) 
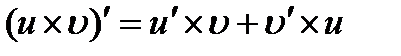, в частности 
;
3) 
;
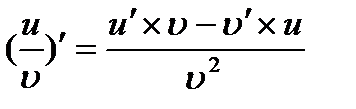4) 
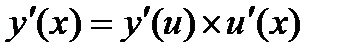, если 
;
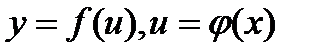5) 
, если 
и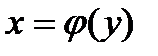 
.
Формулы дифференцирования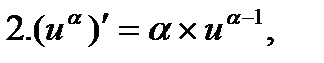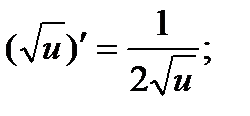
в частности, 
в частности, 
в частности, 
|
|
|
|
|
|
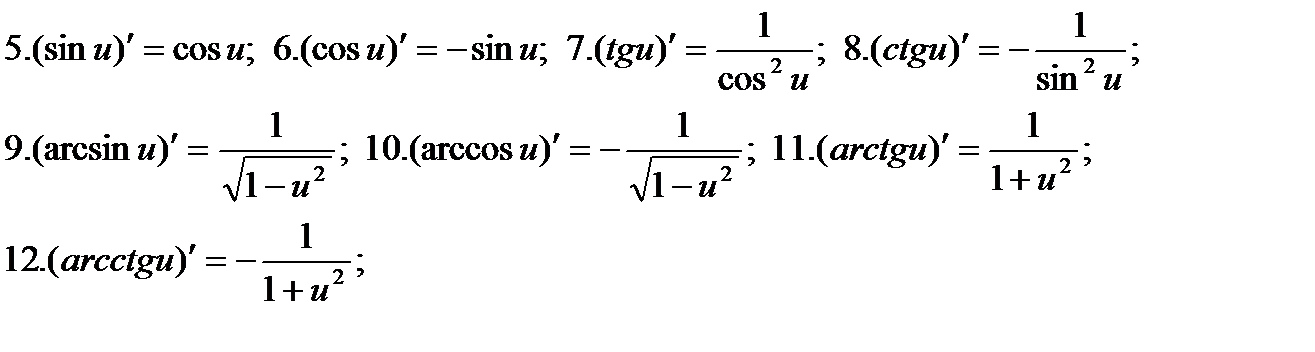
