 |
Показатели вариации в статистике
|
|
|
|
Цель работы – закрепить теоретические знания и приобрести самостоятельные навыки расчёта абсолютных и относительных показателей вариации и анализа полученных результатов.
Литература: Толстик Н.В., Матегорина Н.М. «Статистика», стр. 84-94
Для оценки вариации используются абсолютные и относительные показатели.
К относительным показателям относятся:
коэффициент осцилляции отражает относительную колеблемость крайних значений признака вокруг средней и рассчитывается по формуле:

относительное линейное отклонение характеризует долю усреднённого значения абсолютных отклонений от средней величины и вычисляется по формуле:

коэффициент вариации является наиболее распространённым показателем колеблемости, используемым для оценки типичности средних величин и рассчитывается по формуле:

Чем больший коэффициент вариации, тем менее однородная совокупность и тем менее типична средняя для данной совокупности. Установлено, что совокупность количественно однородна, если коэффициент вариации не превышает 33 %.
К абсолютным показателям относятся: рамах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение.
Абсолютные показатели вариации
| Показатели | Расчётная формула | |
| Данные не сгруппированы | Данные сгруппированы | |
| Размах вариации | 
| 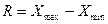
|
| Среднее линейное отклонение | 
| 
|
| Дисперсия | 
 где
где 
| 
 где
где 
|
| Среднее квадратическое отклонение | 
| 
|
Примеры решения задач
|
|
|
Задача.
Имеются следующие данные о чистой прибыли, полученной предприятиями:
| № предприятия | 1 | 2 | 3 | 4 | 5 |
| Чистая прибыль, млн. руб. | 20 | 25 | 30 | 38 | 40 |
Вычислите размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Решение
Для решения задачи воспользуемся вспомогательной таблицей:
| № предприятия | Чистая прибыль, млн. руб. | 
| 
|
| 1 | 20 | 10,6 | 112,36 |
| 2 | 25 | 5,6 | 31,36 |
| 3 | 30 | 0,6 | 0,36 |
| 4 | 38 | 7,4 | 54,76 |
| 5 | 40 | 9,4 | 88,36 |
| Итого: | 153 | 33,6 | 287,2 |
Вычислим среднюю прибыль:

Размах вариации:

Среднее линейное отклонение:

Дисперсия:

Среднее квадратическое отклонение:

Коэффициент вариации:

Средний размер чистой прибыли составляет 30,6 млн. руб. При этом прибыль отдельных предприятий отличается от среднего размера в среднем на 7,5 8млн. руб.
Данная совокупность является однородной, поскольку коэффициент вариации не превышает 33%.
Задания для самостоятельной работы.
Задача 1.
Имеются следующие данные о чистой прибыли, полученной предприятиями:
| № предприятия | 1 | 2 | 3 | 4 | 5 |
| Чистая прибыль, млн. руб. | 30 | 35 | 40 | 48 | 50 |
Вычислите размах вариации, среднее линейное отклонение, дисперсию, среднее квадратическое отклонение и коэффициент вариации.
Задача 2.
Определите среднюю длину пробега автофургона торгово-посреднической фирмы и вычислите: дисперсию, среднее квадратическое отклонение, коэффициент вариации
| Длина пробега за один рейс, км. | 30-50 | 50-70 | 70-90 | 90-110 | 110-130 | 130-150 |
| Число рейсов за квартал | 20 | 25 | 14 | 18 | 9 | 6 |
Задача 3.
В трёх партиях продукции, представленных на контроль качества, было обнаружено:
а) первая партия – 1000 изделий, из них 800 годных, 200 бракованных;
|
|
|
б) вторая партия – 800 изделий, из них 720 годных, 80 бракованных;
в) третья партия – 900 изделий, из них 855 годных и бракованных 45 единиц продукции.
Определите в целом для всей партии следующие показатели:
1) средний процент годной продукции и средний процент брака;
2) дисперсию, среднее квадратическое отклонение и коэффициент вариации годной продукции.
Задачи 4.
Имеются данные о времени обработки деталей рабочими двух бригад.
| Бригады | Время обработки деталей, мин | |||||||||
| I - я бригада | 74 | 86 | 112 | 116 | 132 | 134 | 155 | 183 | - | - |
| II - я бригада | 108 | 113 | 114 | 121 | 122 | 126 | 130 | 132 | 135 | 139 |
1. Определите показатели центральной тенденции (среднюю величину и медиану).
2. Определите показатели вариации.
Задача 5.
Сравните вариацию урожайности зерновых культур и картофеля в хозяйствах региона по средним арифметическим взвешенным на основе следующих данных.
| № хозяйства | Урожайность, ц/га | Посевная площадь, га | ||
| зерновых У | картофеля X | зерновых У | картофеля X | |
| 1 | 15 | 170 | 20 | 10 |
| 2 | 20 | 90 | 30 | 20 |
| 3 | 13 | 130 | 10 | 50 |
| 4 | 17 | 150 | 90 | 40 |
| 5 | 25 | 120 | 50 | 30 |
| 6 | 14 | 80 | 20 | 25 |
| 7 | 16 | 60 | 32 | 20 |
| 8 | 27 | 160 | 48 | 45 |
| 9 | 33 | 140 | 25 | 70 |
| 10 | 30 | 100 | 30 | 35 |
| Итого | 355 | 345 | ||
Задача 6.
Имеются данные о распределении рабочих предприятий по возрасту.
| Группы рабочих по возрасту, лет | Число рабочих f, | Накопленные частоты S |
| 18-20 | 1 | 1 |
| 20-22 | 3 | 4 |
| 22-24 | 6 | 10 |
| 24-26 | 10 | 20 |
| 26-28 | 5 | 25 |
| 28-30 | 3 | 28 |
| 30-32 | 2 | 30 |
| 32-34 | 2 | 32 |
| Итого | 32 |
1. Определите показатели центральной тенденции.
2. Определите показатели вариации.
Задача 7.
Сравните вариацию урожайности зерновых культур и картофеля в хозяйствах региона на основе следующих данных.
| № хозяйства | Урожайность, ц/га | Посевная площадь, га | ||
| зерновых У | картофеля X | зерновых У | картофеля X | |
| 1 | 15 | 170 | 20 | 10 |
| 2 | 20 | 90 | 30 | 20 |
| 3 | 13 | 130 | 10 | 50 |
| 4 | 17 | 150 | 90 | 40 |
| 5 | 25 | 120 | 50 | 30 |
| 6 | 14 | 80 | 20 | 25 |
| 7 | 16 | 60 | 32 | 20 |
| 8 | 27 | 160 | 48 | 45 |
| 9 | 33 | 140 | 25 | 70 |
| 10 | 30 | 100 | 30 | 35 |
| Итого | 355 | 345 | ||
Задача 8.
Имеются следующие данные об успеваемости 20 студентов группы по теории статистики в зимнюю сессию 2010 г.:
| Порядковый номер студента | Балл |
| 1 | 5 |
| 2 | 3 |
| 3 | 5 |
| 4 | 5 |
| 5 | 5 |
| 6 | 5 |
| 7 | 4 |
| 8 | 5 |
| 9 | 2 |
| 10 | 5 |
| 11 | 3 |
| 12 | 4 |
| 13 | 2 |
| 14 | 5 |
| 15 | 3 |
| 16 | 2 |
| 17 | 5 |
| 18 | 4 |
| 19 | 4 |
| 20 | 5 |
Постройте:
|
|
|
а) ряд распределения студентов по баллам оценок, полученных в сессию;
б) ряд распределения студентов по уровню успеваемости, выделив в нем две группы студентов: неуспевающие (2 балла), успевающие (3 балла и выше);
в) укажите, каким видом ряда распределения (вариационным или атрибутивным) является каждый из этих двух рядов.
Задача 9.
Известны следующие данные о результатах сдачи 28 абитуриентами вступительных экзаменов на 1-й курс колледжа в 1999 г. (баллов):
| 10 | 8 | 7 | 10 | 7 | 9 | 10 |
| 8 | 5 | 10 | 9 | 8 | 5 | 9 |
| 7 | 9 | 6 | 5 | 10 | 10 | 8 |
| 8 | 6 | 9 | 7 | 9 | 7 | 9 |
Постройте:
а) ряд распределения абитуриентов по результатам сдачи ими вступительных экзаменов, выделив 4 группы абитуриентов с равными интервалами;
б) ряд, делящий абитуриентов на поступивших и не поступивших в ВУЗ, учитывая, что проходной балл составил 15 баллов. Укажите, по какому группировочному признаку построен каждый из этих рядов распределения: атрибутивному или количественному.
Задача 10.
По данным обследования получено следующее распределение студентов-заочников по возрасту на разных факультетах.
| Возраст студента, лет | Число студентов на факультетах | |||
| экономический | юридический | естествознания | исторический | |
| 20-25 | 200 | 300 | 100 | 50 |
| 26-30 | 900 | 800 | 300 | 150 |
| 31-35 | 700 | 850 | 320 | 230 |
| 36-40 | 70 | 100 | 80 | 250 |
| > 45 | 10 | 5 | 3 | 8 |
Рассчитайте на каждом факультете:
♦ средний возраст студента-заочника;
♦ моду;
♦ медиану;
♦ показатели вариации.
2. Сформулируйте соответствующие выводы.
Задача 11.
В результате выборочного обследования трех ткацких фабрик получено распределение рабочих по выполнению норм выработки.
1. Рассчитайте по каждой фабрике:
♦ в среднем процент выполнения нормы выработки;
♦ модальное значение;
♦ медиану;
♦ показатели вариации.
2. Сформулируйте соответствующие выводы.
| Выполнение | Число рабочих на фабриках | ||
| I | II | III | |
| До 1000 | 9 | 10 | 12 |
| 100-105 | 14 | 22 | 35 |
| 105- по | 28 | 35 | 20 |
| 110-115 | 31 | 27 | 11 |
| > 115 | 8 | 5 | 3 |
|
|
|


