Расчет и построение доверительного интервала для генеральной средней арифметической

Так как распределение выборки d, составленной из разностей парных значений, отличается от нормального закона распределения, а генеральная дисперсия d_i неизвестна, приблизительные значения границ доверительного интервала, в котором с доверительной вероятностью P будет находиться среднее арифметическое значение генеральной совокупности , найдем из следующего двойного неравенства:

Для рассматриваемой задачи оно будет иметь вид:

По таблице критерия Стьюдента (Приложение 4) мы нашли, что для уровня значимости a = 0,05, числа степеней свободы k = n – 1 = 10 – 1 = 9 и двухсторонней критической области t_a = 2,26.

Стандартную ошибку среднего арифметического найдем по формуле:

уд.

Доверительный интервал для среднего арифметического прироста количества ударов за 10 с в генеральной совокупности равен:

– 1,25 уд. 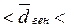6,65 уд.

Следовательно, с доверительной вероятностью P = 0,95 можно утверждать, что в результате тренировки улучшение показателя скоростных качеств будет находиться в пределах от – 1,25 до 6,65 ударов за 10 с.

Для построения доверительного интервала необходимо выбрать масштаб. Выберем масштаб 1 уд. ≡ 1 см.

 

Доверительный интервал для

ПРИЛОЖЕНИЯ

 

Приложение 1 – Критические точки распределения коэффициента корреляции. Односторонняя критическая область

n	α	n	α
0,05	0,01	0,05	0,01
	0,988	0,9995		0,400	0,543
	0,900	0,980		0,389	0,529
	0,805	0,934		0,378	0,516
	0,729	0,882		0,369	0,503
	0,669	0,833		0,360	0,492
	0,621	0,789		0,323	0,445
	0,582	0,750		0,296	0,409
	0,549	0,715		0,275	0,381
	0,521	0,685		0,257	0,358
	0,497	0,658		0,243	0,338
	0,476	0,634		0,231	0,322
	0,457	0,612		0,211	0,295
	0,441	0,592		0,195	0,274
	0,426	0,574		0,183	0,257
	0,412	0,558		0,173	0,242
				0,164	0,230

 

Двусторонняя критическая область

n	α	N	Α
0,05	0,01	0,05	0,01
	0,950	0,990		0,388	0,496
	0,878	0,959		0,381	0,487
	0,811	0,917		0,374	0,476
	0,754	0,874		0,367	0,470
	0,707	0,834		0,361	0,463
	0,666	0,798		0,322	0,435
	0,632	0,766		0,310	0,407
	0,602	0,736		0,292	0,384
	0,576	0,708		0,277	0,364
	0,553	0,684		0,253	0,333
	0,532	0,661		0,234	0,308
	0,514	0,644		0,219	0,288
	0,497	0,623		0,206	0,272
	0,482	0,606		0,196	0,258
	0,468	0,590		0,175	0,230
n	Α	n	Α
0,05	0,01	0,05	0,01
	0,456	0,575		0,160	0,210
	0,444	0,561		0,138	0,182
	0,433	0,549		0,124	0,163
	0,423	0,537		0,113	0,148
	0,413	0,526		0,098	0,128
	0,404	0,515		0,088	0,115
	0,396	0,505		0,062	0,081

 

Приложение 2 – Значения коэффициентов a_nk, используемых для расчета критерия W проверки нормальности распределения

k	n
	0,7071	0,6872	0,6646	0,6431	0,6233	0,6052	0,5888	0,5739
		0,1677	0,2413	0,2806	0,3031	0,3164	0,3244	0,3291
				0,0875	0,1401	0,1743	0,1976	0,2141
						0,0561	0,0947	0,1224
								0,0399
k	n
	0,5601	0,5475	0,5359	0,5251	0,5150	0,5056	0,4968	0,4886
	0,3315	0,3325	0,3325	0,3318	0,3306	0,3290	0,3273	0,3253
	0,2260	0,2347	0,2412	0,2460	0,2495	0,2521	0,2540	0,2553
	0,1429	0,1585	0,1707	0,1802	0,1878	0,1939	0,1988	0,2027
	0,0695	0,0922	0,1099	0,1240	0,1353	0,1447	0,1524	0,1587
		0,0303	0,0539	0,0727	0,0880	0,1005	0,1109	0,1197
				0,0240	0,0433	0,0593	0,0725	0,0837
						0,0196	0,0359	0,0496
								0,0163
k	n
	0,4808	0,4734	0,4643	0,4590	0,4542	0,4493	0,4450	0,4407
	0,3232	0,3211	0,3185	0,3156	0,3126	0,3098	0,3069	0,3043
	0,2561	0,2565	0,2578	0,2571	0,2563	0,2554	0,2543	0,2533
	0,2059	0,2085	0,2119	0,2131	0,2139	0,2145	0,2148	0,2151
	0,1641	0,1686	0,1736	0,1764	0,1787	0,1807	0,1822	0,1836
	0,1271	0,1334	0,1399	0,1443	0,1480	0,1512	0,1539	0,1563
	0,0932	0,1013	0,1092	0,1150	0,1201	0,1245	0,1283	0,1316
k	n
	0,0612	0,0711	0,0804	0,0878	0,0941	0,0997	0,1046	0,1089
	0,0303	0,0422	0,0530	0,0616	0,0696	0,0764	0,0823	0,0876
		0,0140	0,0263	0,0368	0,0549	0,0539	0,0610	0,0672
				0,0122	0,0228	0,0321	0,0403	0,0476
						0,0107	0,0200	0,0284
								0,0094
k	n
	0,4366	0,4328	0,4291	0,4254	0,4220	0,4188	0,4156	0,4127
	0,3018	0,2992	0,2988	0,2944	0,2921	0,2898	0,2876	0,2854
	0,2522	0,2510	0,2499	0,2487	0,2475	0,2463	0,2451	0,2439
	0,2152	0,2151	0,2150	0,2148	0,2145	0,2141	0,2137	0,2132
	0,1848	0,1867	0,1864	0,1870	0,1874	0,1878	0,1880	0,1882
	0,1584	0,1601	0,1616	0,1630	0,1641	0,1651	0,1660	0,1667
	0,1346	0,1372	0,1396	0,1415	0,1433	0,1449	0,1463	0,1475
	0,1128	0,1162	0,1192	0,1219	0,1243	0,1265	0,1284	0,1301
	0,0923	0,0955	0,1002	0,1036	0,1066	0,1093	0,1118	0,1140
	0,0728	0,0778	0,0822	0,0862	0,0899	0,0931	0,0961	0,0988
	0,0540	0,0598	0,0650	0,0697	0,0739	0,0777	0,0812	0,0844
	0,0358	0,0424	0,0483	0,0537	0,0585	0,0629	0,0669	0,0706
	0,0178	0,0253	0,0320	0,0381	0,0435	0,0485	0,0530	0,0572
		0,0084	0,0159	0,0227	0,0289	0,0344	0,0395	0,0441
				0,0076	0,0144	0,0206	0,0262	0,0314
						0,0068	0,0131	0,0187
								0,0062
k	n
	0,4096	0,4068	0,4040	0,4015	0,3989	0,3964	0,3940	0,3917
	0,2834	0,2813	0,2794	0,2774	0,2755	0,2737	0,2719	0,2701
	0,2427	0,2415	0,2403	0,2391	0,2380	0,2368	0,2357	0,2345
	0,2127	0,2121	0,2116	0,2110	0,2104	0,2098	0,2091	0,2085
	0,1883	0,1883	0,1883	0,1881	0,1880	0,1878	0,1876	0,1874
	0,1673	0,1678	0,1683	0,1686	0,1689	0,1691	0,1693	0,1694
	0,1487	0,1496	0,1505	0,1513	0,1520	0,1526	0,1531	0,1535
	0,1317	0,1331	0,1344	0,1356	0,1366	0,1376	0,1384	0,1392
	0,1160	0,1179	0,1196	0,1211	0,1225	0,1237	0,1249	0,1259
	0,1013	0,1036	0,1056	0,1075	0,1092	0,1108	0,1123	0,1136
	0,0873	0,9000	0,0924	0,0947	0,0967	0,0986	0,1004	0,1020
k	n
	0,0739	0,0770	0,0798	0,0824	0,0848	0,0870	0,0891	0,0909
	0,0610	0,0645	0,0677	0,0706	0,0733	0,0759	0,0782	0,0804
	0,0484	0,0523	0,0559	0,0592	0,0622	0,0651	0,0677	0,0701
	0,0361	0,0404	0,0444	0,0481	0,0515	0,0546	0,0575	0,0602
	0,0239	0,0287	0,0331	0,0372	0,0409	0,0444	0,0476	0,0506
	0,0119	0,0172	0,0220	0,0264	0,0305	0,0343	0,0379	0,0411
		0,0057	0,0110	0,0156	0,0202	0,0244	0,0283	0,0318
				0,0053	0,0101	0,0146	0,0188	0,0227
						0,0049	0,0094	0,0136
								0,0045
k	n
	0,3894	0,3872	0,3850	0,3830	0,3808	0,3789	0,3770	0,3751
	0,2684	0,2667	0,2651	0,2635	0,2620	0,2604	0,2589	0,2574
	0,2334	0,2323	0,2312	0,2302	0,2291	0,2281	0,2271	0,2260
	0,2078	0,2072	0,2065	0,2058	0,2052	0,2045	0,2038	0,2032
	0,1871	0,1868	0,1865	0,1862	0,1859	0,1855	0,1851	0,1847
	0,1695	0,1695	0,1695	0,1695	0,1695	0,1693	0,1692	0,1691
	0,1539	0,1542	0,1545	0,1548	0,1550	0,1551	0,1553	0,1554
	0,1398	0,1405	0,1410	0,1416	0,1420	0,1423	0,1427	0,1430
	0,1269	0,1278	0,1286	0,1293	0,1300	0,1306	0,1312	0,1317
	0,1149	0,1160	0,1170	0,1180	0,1189	0,1197	0,1205	0,1212
	0,1035	0,1049	0,1062	0,1073	0,1085	0,1095	0,1105	0,1113
	0,0927	0,0943	0,0959	0,0972	0,0986	0,0998	0,1010	0,1020
	0,0824	0,0842	0,0860	0,0876	0,0882	0,0906	0,0919	0,0932
	0,0724	0,0745	0,0765	0,0783	0,0801	0,0817	0,0832	0,0846
	0,0628	0,0651	0,0673	0,0694	0,0713	0,0731	0,0748	0,0764
	0,0534	0,0560	0,0584	0,0607	0,0628	0,0648	0,0667	0,0685
	0,0442	0,0471	0,0497	0,0522	0,0546	0,0568	0,0588	0,0608
	0,0352	0,0383	0,0412	0,0439	0,0465	0,0489	0,0511	0,0532
	0,0263	0,0296	0,0328	0,0357	0,0385	0,0411	0,0436	0,0459
	0,0175	0,0211	0,0245	0,0277	0,0307	0,0335	0,0361	0,0386
	0,0087	0,0126	0,0163	0,0197	0,0229	0,0259	0,0288	0,0314
		0,0042	0,0081	0,0118	0,0153	0,0185	0,0215	0,0244
				0,0039	0,0076	0,0111	0,0143	0,0174
						0,0037	0,0071	0,0104
								0,0035

 

Приложение 3 – Критические точки распределения критерия W Шапиро и Уилка, используемого для проверки гипотезы о нормальном распределении генеральной совокупности

n	α	n	α	n	α
0,05	0,01	0,05	0,01	0,05	0,01
	0,767	0,753		0,901	0,863		0,934	0,910
	0,748	0,687		0,905	0,868		0,935	0,912
	0,762	0,686		0,908	0,873		0,936	0,914
	0,786	0,713		0,911	0,878		0,938	0,916
	0,803	0,730		0,914	0,881		0,939	0,917
	0,818	0,749		0,916	0,884		0,940	0,919
	0,829	0,764		0,918	0,888		0,941	0,920
	0,842	0,791		0,920	0,891		0,942	0,922
	0,850	0,792		0,923	0,894		0,943	0,923
	0,859	0,805		0,924	0,896		0,944	0,924
	0,866	0,814		0,926	0,898		0,945	0,926
	0,874	0,825		0,927	0,900		0,945	0,927
	0,881	0,835		0,929	0,902		0,946	0,928
	0,887	0,844		0,930	0,904		0,947	0,929
	0,892	0,851		0,931	0,906		0,947	0,929
	0,897	0,858		0,933	0,908		0,947	0,950

 

Приложение 4 – Критические точки распределения критерия t Стьюдента

Число степеней свободы k	Уровень значимости α (двусторонняя критическая область)
0,10	0,05	0,02	0,01	0,002	0,001
	6,31	12,71	31,82	63,66	318,31	636,62
	2,92	4,30	6,96	9,92	22,33	31,60
	2,35	3,18	4,54	5,84	10,21	12,92
	2,13	2,78	3,75	4,60	7,17	8,61
	2,02	2,57	3,36	4,03	5,89	6,87
	1,94	2,45	3,14	3,71	5,21	5,96
	1,89	2,36	3,00	3,50	4,79	5,41
	1,86	2,31	2,90	3,36	4,50	5,04
	1,83	2,26	2,82	3,25	4,30	4,78
	1,81	2,23	2,76	3,17	4,14	4,59
	1,80	2,20	2,72	3,11	4,02	4,44
	1,78	2,18	2,68	3,05	3,93	4,32
	1,77	2,16	2,65	3,01	3,85	4,22
	1,76	2,14	2,62	2,98	3,79	4,14
	1,75	2,13	2,60	2,95	3,73	4,07
Число степеней свободы k	Уровень значимости α (двусторонняя критическая область)
0,10	0,05	0,02	0,01	0,002	0,001
	1,75	2,12	2,58	2,92	3,69	4,01
	1,74	2,11	2,57	2,90	3,65	3,97
	1,73	2,10	2,55	2,88	3,61	3,92
	1,73	2,09	2,54	2,86	3,58	3,88
	1,72	2,09	2,53	2,85	3,55	3,85
	1,72	2,08	2,52	2,83	3,53	3,82
	1,72	2,07	2,51	2,82	3,50	3,79
	1,71	2,07	2,50	2,81	3,48	3,77
	1,71	2,06	2,49	2,80	3,47	3,75
	1,71	2,06	2,49	2,79	3,45	3,73
	1,71	2,06	2,48	2,78	3,43	3,71
	1,70	2,05	2,47	2,77	3,42	3,69
	1,70	2,05	2,47	2,76	3,41	3,67
	1,70	2,05	2,46	2,76	3,40	3,66
	1,70	2,04	2,46	2,75	3,39	3,65
	1,68	2,02	2,42	2,70	3,31	3,55
	1,67	2,00	2,39	2,66	3,23	3,46
	1,66	1,98	2,36	2,62	3,16	3,37
∞	1,64	1,96	2,33	2,58	3,09	3,29
0,05	0,025	0,01	0,005	0,001	0,0005
Уровень значимости α (односторонняя критическая область)

 

Приложение 5 – Критические точки распределения критерия Уилкоксона, используемого для сравнения двух попарно зависимых выборок

n	α	n	α	n	α
0,05	0,01	0,05	0,01	0,05	0,01
		–
		–

 

Приложение 6 – Некоторые статистические функции табличного процессора Microsoft Excel

Функция	Описание
ДИСП	Оценивает дисперсию по выборке (логические значения и текст игнорируются).
ДОВЕРИТ	Возвращает доверительный интервал для среднего генеральной совокупности.
КВАДРОТКЛ	Возвращает сумму квадратов отклонений точек данного от среднего по выборке.
КОРРЕЛ	Возвращает коэффициент корреляции между двумя множествами данных.
МАКС	Возвращает максимальное значение из списка аргументов. Логические значения или текст игнорируются.
МЕДИАНА	Возвращает медиану исходных чисел.
МИН	Возвращает минимальное значение из списка аргументов. Логические значения или текст игнорируются.
МОДА	Возвращает значение моды множества данных.
ПИРСОН	Возвращает коэффициент корреляции Пирсона, r.
СРЗНАЧ	Возвращает среднее (арифметическое) своих аргументов, которые могут быть числами или именами, массивами или ссылками на ячейки с числами.
СТАНДОТКЛОН	Оценивает стандартное отклонение по выборке. Логические значения или текст игнорируются.
СТЬЮДРАСПОБР	Возвращает обратное распределение Стьюдента.
СЧЁТ	Подсчитывает количество чисел в списке аргументов.

 

Литература

1. Годик, М.А. Спортивная метрология: учеб. для ин-тов физ. культуры / М.А. Годик. М., 1988.

2. Основы математической статистики: уч. пособие для ин-тов физ. культуры / под общ. ред. В.С. Иванова. М., 1990.

3. Спортивная метрология: учеб. для ин-тов физ. культуры / под общ. ред. В.М. Зациорского. М., 1982.

4. Основы педагогических измерений. Вопросы разработки и использования педагогических тестов: учеб.-метод. пособие / под общ. ред. В.Д. Скаковского. Минск, 2009.

5. Гинзбург, Г.И. Расчетно-графические работы по спортивной метрологии / Г.И. Гинзбург, В.Г. Киселев. Минск, 1984.

 

СОДЕРЖАНИЕ

Предисловие...........................................................................................….... 3

I этап деловой игры. КОНТРОЛЬ И ИЗМЕРЕНИЯ В СПОРТЕ........... 6

1. Контроль в физическом воспитании и спорте……............................. 6

2. Основные понятия теории тестов……................................................. 8

3. Основные понятия теории измерений................................................. 8

3.1. Шкалы измерений….................................................................... 9

3.2. Единицы измерений................................................................... 10

3.3. Точность измерений................................................................... 11

4. Игровая ситуация и организация игры на I этапе............................. 14

5. Порядок работы на I этапе................................................................. 17

II этап деловой игры. МАТЕМАТИЧЕСКИЕ МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ В СПОРТЕ......................................................................... 20

1. Ситуация и организация игры на II этапе.......................................... 20

2. Предмет математической статистики………………………………. 21

3. Составление рядов распределения и их графические представления………………………………………………………... 21

4. Меры центральной тенденции………………………………………. 25

5. Выбор меры центральной тенденции………………………………. 26

6. Характеристики вариации…………………………………………… 27

7. Репрезентативность выборочных показателей…………………….. 29

8. Ошибки репрезентативности………………………………………... 29

9. Стандартная ошибка среднего арифметического………………….. 30

10. Показатель точности оценки параметров…………………………. 32

11. Порядок работы на II этапе………………………………………… 32

III этап деловой игры. ОЦЕНКА НАДЕЖНОСТИ ТЕСТА ДЛЯ КОНТРОЛЯ ЗА РАЗВИТИЕМ СКОРОСТНЫХ КАЧЕСТВ ………… 41

1. Модель ситуации и организация игры на III этапе………………… 41

2. Основы теории корреляции…………………………………………. 41

2.1. Функциональная и статистическая взаимосвязи…………….. 41

2.2. Корреляционное поле………………………………………….. 42

2.3. Оценка тесноты взаимосвязи………………………………….. 44

2.4. Направленность взаимосвязи…………………………………. 45

2.5. Методы вычисления коэффициентов взаимосвязи………….. 46

3. Основы теории проверки статистических гипотез………………… 47

3.1. Проверка нулевых гипотез…………………………………….. 48

3.2. Односторонние и двусторонние критические области……… 49

3.3. Ошибочные решения при проверке гипотез…………………. 49

3.4. Основные этапы проверки статистических гипотез………… 50

3.5. Оценка статистической достоверности коэффициента корреляции…………………………………………………………... 51

 

4. Надежность тестов…………………………………………………… 51

4.1. Понятие надежности тестов…………………………………… 51

4.2. Стабильность теста…………………………………………….. 53

4.3. Согласованность теста…………………………………………. 54

4.4. Эквивалентность тестов……………………………………….. 54

4.5. Пути повышения надежности теста…………………………... 55

5. Порядок работы на III этапе…………………………………………. 56

IV этап деловой игры. ОЦЕНКА ИНФОРМАТИВНОСТИ ТЕСТА... 60

1. Информативность тестов (основные понятия)……………………... 60

2. Эмпирическая информативность (существует измеряемый критерий)………………………………………...……………………. 61

3. Эмпирическая информативность в практической работе…………. 63

4. Содержательная (логическая) информативность…………………... 63

5. Ситуация и организация игры на IV этапе…………………………. 64

V этап деловой игры. ОЦЕНКА ЭФФЕКТИВНОСТИ МЕТОДИКИ ТРЕНИРОВКИ ……………………………………………………………... 68

1. Ситуация и организация игры на V этапе………………………...... 68

2. Выбор критерия для оценки эффективности………………………. 69

3. Нормальный закон распределения результатов измерений………. 69

4. Основные свойства кривой нормального распределения…………. 71

5. Влияние и σ на вид кривой нормального распределения………. 72

6. Вероятность попадания в области , , . Правило трех сигм……………………………………………………………………. 73

7. Интервальные оценки параметров генеральной совокупности…... 74

7.1. Доверительный интервал. Доверительная вероятность……... 74

7.2. Построение доверительного интервала для оценки среднего значения генеральной совокупности……………………………… 75

8. Порядок работы на V этапе………………………………………….. 76

Приложения…………………………………………………………………. 85

Литература…………………………………………………………………... 92

⇐ Предыдущая567891011121314

Поделиться:

Воспользуйтесь поиском по сайту: