 |
Алгебра логики
|
|
|
|
Математическая логика – это раздел математики, в котором изучается доказуемость математических суждений и принципы доказуемости в математике.
Суждение в математической логике – это заключение об объекте, его свойстве или отношениях между объектами. Суждение является смыслом высказывания.
Высказывание в математической логике – это предложение, выражающее суждение. Если суждение истинно, то истинно и высказывание, а если суждение ложно, то и высказывание ложно. Истинность и ложность – это логические (истинностные) значения высказываний. Высказывание может быть только повествовательным предложением, так как оценка истинности или ложности других предложений (например, вопросительных) невозможна. Высказывание иначе называется выражение.
Алгебра логики (алгебра высказываний) – это раздел математической логики, в котором изучаются различные логические операции над высказываниями. Алгебра логики использует двоичную (бинарную) логику, то есть в её основу составляют две оценки высказывания: истина (или логическая единица) и ложь (или логический ноль).
Логическое высказывание в программировании – это простая конструкция языка программирования, в результате вычисления которой даётся оценка (истина или ложь). Над простыми логическими высказываниями можно проводить логические операции, в результате вычисления которых также даётся оценка (истина или ложь). Логические высказывания, объединённые логическими операциями, называются сложные логические высказывания.
Логический элемент компьютера – это электронная схема (логический вентиль), которая предназначена для обработки информации. Логические элементы позволяют реализовывать логические функции (последовательности логических операций), которые описывают работу устройств компьютера. Обычно логический элемент имеет несколько входов (например, от двух до восьми) и один или несколько выходов (например, два). Информация представляется в виде дискретного сигнала или последовательности сигналов, каждый из которых имеет один из двух установленных уровней в двоичной логике (как правило, это уровни напряжений): высокий или низкий уровень. Установленные уровни соответствуют двум логическим состояниям: высокий уровень сигнала обычно соответствует значению истина (или логическая единица), а низкий уровень сигнала обычно соответствует значению ложь (или логический ноль). Каждый логический элемент компьютера имеет определённое условное обозначение, выражающее реализуемую им логическую функцию. Работа логических элементов описывается с помощью различных таблиц истинности.
|
|
|
Таблица истинности – это формализованное представление работы логической операции (последовательности логических операций), которое позволяет описать работу логических элементов компьютера. Таблица истинности устанавливает все возможные соответствия между значениями входных сигналов (операндов) логического элемента и значениями выходного сигнала (результата операции) с точки зрения истинности: истина (логическая единица) или ложь (логический ноль). Истинность логического высказывания определяется посредством построения таблицы истинности этого высказывания (выражения). Для любого логического высказывания можно построить соответствующую ему таблицу истинности, для этого нужно применить законы алгебры логики и значения таблиц истинности для простых логических высказываний. Для любой таблицы истинности можно составить соответствующее ей логическое высказывание, для этого из таблицы истинности выбираются наборы переменных, для которых значение логического выражения равно логической единице, а затем для каждого такого набора переменных записывается их конъюнкция (если значение переменной равно логической единице, то включаем саму переменную, а если значение переменной равно логическому нулю, то включаем её отрицание), после чего все конъюнкции связываются операциями дизъюнкции. Полученное логическое высказывание, как правило, необходимо упростить.
|
|
|
Упрощение логических высказываний – это применение к данному логическому высказыванию законов алгебры логики (свойств логических операций) и определение значений истинности частей высказывания в соответствии с таблицами истинности.
Логическое отрицание (инверсия, НЕ) – это логическая операция над высказыванием, результатом вычисления которой является высказывание, значение которого противоположно логическому состоянию исходного высказывания. Для высказывания  логическое отрицание обозначается:
логическое отрицание обозначается: 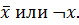 Другие обозначения (в программировании):
Другие обозначения (в программировании):  Для логического элемента, реализовывающего логическую операцию НЕ, связь между входным
Для логического элемента, реализовывающего логическую операцию НЕ, связь между входным  и выходным
и выходным  сигналами определяется соотношением:
сигналами определяется соотношением: 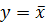 . Это означает, что если на входе схемы логический ноль, то на выходе схемы будет логическая единица, а если на входе схемы логическая единица, то на выходе схемы будет логический ноль.
. Это означает, что если на входе схемы логический ноль, то на выходе схемы будет логическая единица, а если на входе схемы логическая единица, то на выходе схемы будет логический ноль.
Таблица истинности операции НЕ имеет вид:
| x | y |
Логическое сложение (дизъюнкция, ИЛИ) – это логическая операция над высказываниями, результатом вычисления которой является высказывание, значение которого равно наибольшему логическому состоянию среди исходных высказываний. Для высказываний 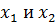 логическое сложение обозначается:
логическое сложение обозначается: 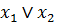 или
или  Другие обозначения (в программировании):
Другие обозначения (в программировании):  Для логического элемента, реализовывающего логическую операцию ИЛИ, связь между входными
Для логического элемента, реализовывающего логическую операцию ИЛИ, связь между входными 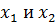 и выходным
и выходным  сигналами определяется соотношением:
сигналами определяется соотношением:  . Это означает, что на выходе схемы будет логический ноль, если на всех входах схемы будут логические нули, а если даже на одном входе схемы будет логическая единица, то на выходе схемы также будет логическая единица.
. Это означает, что на выходе схемы будет логический ноль, если на всех входах схемы будут логические нули, а если даже на одном входе схемы будет логическая единица, то на выходе схемы также будет логическая единица.
Таблица истинности операции ИЛИ имеет вид:
| x1 | x2 | y |
Логическое умножение (конъюнкция, И) – это логическая операция над высказываниями, результатом вычисления которой является высказывание, значение которого равно наименьшему логическому состоянию среди исходных высказываний. Для высказываний 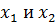 логическое умножение обозначается:
логическое умножение обозначается:  Другие обозначения (в программировании):
Другие обозначения (в программировании):  Для логического элемента, реализовывающего логическую операцию И, связь между входными
Для логического элемента, реализовывающего логическую операцию И, связь между входными 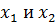 и выходным
и выходным  сигналами определяется соотношением:
сигналами определяется соотношением:  . Это означает, что на выходе схемы будет логическая единица, если на всех входах схемы будут логические единицы, а если даже на одном входе схемы будет логический ноль, то на выходе схемы также будет логический ноль.
. Это означает, что на выходе схемы будет логическая единица, если на всех входах схемы будут логические единицы, а если даже на одном входе схемы будет логический ноль, то на выходе схемы также будет логический ноль.
|
|
|
Таблица истинности операции И имеет вид:
| x1 | x2 | y |
Основные законы алгебры логики:
· закон двойного отрицания:  ,
,
· закон исключённого третьего для операции ИЛИ: 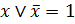 ,
,
· закон противоречия для операции И:  ,
,
· переместительный (коммутативный) закон для операций ИЛИ и И:  а также
а также  ,
,
· сочетательный (ассоциативный) закон для операций ИЛИ и И:  а также
а также 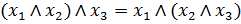 ,
,
· распределительный (дистрибутивный) закон для операций ИЛИ и И:  а также
а также  ,
,
· закон идемпотентности (отсутствия коэффициентов и степеней) для операций ИЛИ и И:  , а также
, а также  ,
,
· закон поглощения для операций ИЛИ и И: 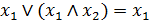 , а также
, а также  ,
,
· закон де Моргана для операций ИЛИ и И:  , а также
, а также  .
.
|
|
|


