 |
Точность вычислений, классификация погрешностей.
|
|
|
|
В. Пикулев.
Методы компьютерных вычислений
и их приложение к физическим задачам.
Методическое пособие
Петрозаводск, 2004
1. Всякий специалист стремится достичь
своего уровня некомпетентности.
2. Компьютер – средство многократного
увеличения некомпетентности человека.
3. Если две ошибки не принесли результата
– испробуй третью.
Лоуренс Питер, «Иерархиология».
Введение в предмет
Численные методы – раздел математики, который со времен Ньютона и Эйлера до настоящего времени находит очень широкое применение в прикладной науке. Традиционно физика является основным источником задач построения математических моделей, описывающих явления окружающего мира, она же является основным потребителем алгоритмов и программ, позволяющих эти задачи с определенным успехом решать.
При этом задачей физика является не только правильный выбор программы, которая призвана решать физическую проблему, но и подробный анализ и корректировка используемых алгоритмов, в соответствии с реалиями поставленной задачи и теми математическими правилами, которые либо допускают существование решения с заданной точностью, либо говорят о невозможности такого решения.
Примеры современных физических задач, для решения которых используются численные методы – моделирование астрономических событий (рождение и развитие Вселенной), моделирование процессов в микромире (распад и синтез частиц), моделирование установок и процессов термоядерного синтеза. Более «прикладные» задачи – моделирование физических процессов в твердотельных структурах (широко используется в проектировании и изготовлении интегральных схем), моделирование процессов в газах и плазме. Учитывая большую сложность и дороговизну современных экспериментальных методик, и, с другой стороны, постоянный рост производительности вычислительных систем, нетрудно определить тенденцию к увеличению в настоящее время доли модельных (вычислительных) экспериментов. Большое количество численных методов разработано для решения задач математической физики, к которым, например, относятся задачи тепло- и массопереноса, исследования турбулентного движения.
|
|
|
К инженерным приложениям численных методов можно отнести расчеты магнитных и электростатических линз для заряженных частиц, различного рода радиотехнические расчеты, включая, например, проектирование СВЧ-волноводов. Любопытно, что как в теоретической физике, так и в инженерной практике решаются численными методами различные задачи теоретической механики, например, задачи столкновения (в том числе динамический хаос). Естественно, такое приложение вычислительной техники к физике, как управление экспериментом и сбор данных, в данном курсе не рассматривается.
План построения вычислительного эксперимента:
1) Создание модели, фиксирующей главные исследуемые факторы. Одновременно формулируются рамки применимости модели.
2) Предварительное исследование математической модели: поверка корректности постановки задачи, существования и единственности решения.
3) Разработка метода расчета сформулированной задачи, построение эффективных вычислительных алгоритмов.
4) Создание программы, осуществляющей моделирование физического объекта, включающей в себя реализации используемых численных методов, проверки корректности ввода исходных и вывода результирующих данных
5) Сравнение полученных результатов моделирования с тестовыми примерами и экспериментальными данными; решение вопроса о правильности практического моделирования (иначе повторяются пункты 3 и 4).
|
|
|
6) Решение вопроса о достоверности предложенной математической модели. Если модель не описывает экспериментальные данные, возврат на пункт 1.
Таким образом, численный эксперимент – это не однократное вычисление по некоторому набору формул, а многостадийный процесс программирования, анализа результатов и их погрешностей.
Задача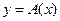 
называется корректно поставленной, если для любых входных данных х из некоторого класса решение y существует, единственно и устойчиво по входным данным.
(Класс может представлять собой координатное бесконечномерное пространство, множество непрерывных функций и др.)
Численный алгоритм – однозначная последовательность действий, которые могут привести к одному решению.
Отсутствие устойчивости обычно означает, что сравнительно небольшой погрешности δ x соответствует весьма большое δ y, а значит получаемое решение будет далеко от истинного. К такой задаче численные методы применять бессмысленно, ибо погрешности численного расчета будут катастрофически нарастать. Устойчивость задачи определяется (1) математической формулировкой, (2) используемым алгоритмом расчета. Пример неустойчивой задачи в первом случае:
Система 
имеет решение 
, однако
Система 
имеет решение 
, то есть разница в коэффициенте менее 1% приводит к изменению решения в 300%.
Пример алгоритмической неустойчивости – вычисление производных численными методами: какой бы метод мы не использовали, приходится вычитать весьма мало различающиеся числа.
В настоящее время развиты методы решения многих некорректных задач, которые основаны на решении вспомогательной корректной задачи, близкой к исходной.
Если выполняется условие для норм (модулей) 
, то задача устойчива. Однако если константа С очень велика, то фактически наблюдается слабая устойчивость. Такую задачу называют плохо обусловленной. Пример – дифференциальное уравнение 
с начальными условиями 
. Общее решение дифференциального уравнения есть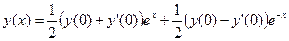 
. Начальные условия приводят к обнулению первого слагаемого, но если из-за погрешности начальных данных это будет не так, то при возрастании x влияние первого слагаемого будет катастрофически нарастать.
|
|
|
Точность вычислений, классификация погрешностей.
Во всех случаях математическая точность решения должна быть в 2-4 раза выше, чем ожидаемая физическая точность модели. Более высокая математическая точность, как и более низкая, будут неадекватны данной модели.
Существуют четыре источника погрешности результата:
1) погрешность математической модели – связана с ее несоответствием физической реальности, так как абсолютная истина недостижима. Если математическая модель выбрана недостаточно тщательно, то, какие бы методы мы не применяли для расчета, все результаты будут недостаточно надежны, а в некоторых случаях и совершенно неправильны.
2) погрешность исходных данных, принятых для расчета. Это неустранимая погрешность, но это погрешность возможно и необходимо оценить для выбора алгоритма расчета и точности вычислений. Как известно, ошибки эксперимента условно делят на систематические, случайные и грубые, а идентификация таких ошибок возможно при статистическом анализа результатов эксперимента.
3) погрешность метода – основана на дискретном характере любого численного алгоритма. Это значит, что вместо точного решения исходной задачи метод находит решение другой задачи, близкого в каком-то смысле (например по норме банахова пространства) к искомому. Погрешность метода – основная характеристика любого численного алгоритма. Погрешность метода должна быть в 2-5 раз меньше неустранимой погрешности.
4) погрешность округления – связана с использованием в вычислительных машинах чисел с конечной точностью представления.
Вот иллюстрация этих определений. Пусть имеется реальный маятник, совершающий затухающие колебания, начинающий движение в момент t = t 0. Требуется найти угол отклонения φ от вертикали в момент t 1. Движение маятника мы можем описать следующим дифференциальным уравнением:
,
где l – длина маятника, g – ускорение силы тяжести, μ – коэффициент трения.
Как только принимается такое описание задачи, решение уже приобретает неустранимую погрешность, в частности потому, что реальное трение зависит от скорости не совсем линейно (погрешность модели). Кроме того, воспроизведя реальный эксперимент, мы зададим l, g (в известной точке планеты), μ с некоторой точностью, и получим набор значений с погрешностью, которую можем оценить из анализа статистики некоторого числа однотипных опытов (погрешность исходных данных). Взятое в модели дифференциальное уравнение нельзя решить в явном виде, для его решения требуется применить какой-либо численный метод, имеющий заранее известную погрешность, которая должна быть меньше неустранимой погрешности. После совершения вычислений мы получим значения с погрешностью большей, нежели погрешность метода, так как к ней прибавится погрешность округления.
|
|
|
Рассмотрим правила расчета погрешности округления:
1) Сложение и вычитание приближенных чисел
Введем в рассмотрение два числа a и b, называемых приближенными, то есть это есть оценка точных значений A и B, известных с абсолютными погрешностями ±εa и ±εb. Знаки этих погрешностей нам неизвестны, следовательно для обеспечения достоверности конечного результата мы должны взять наихудший случай, когда погрешности складываются. Таким образом формулируются следующие правила:
1. Абсолютная погрешность суммы приближенных чисел равна сумме абсолютных погрешностей слагаемых.
2. Абсолютная погрешность разности приближенных чисел равна сумме абсолютных погрешностей слагаемых.
Относительной погрешностью приближенного числа a будет являться величина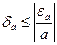 
. По этому же правилу определим относительную погрешность суммы приближенных чисел a и b как 
. При этом можно показать, что
3. Относительная погрешность суммы слагаемых одного знака заключена между наименьшей и наибольшей относительными погрешностями слагаемых: 
.
4. Для разности двух приближенных чисел одного знака величина относительной погрешности 
может быть сколь угодно большой.
2) Умножение и деление приближенных чисел
Очевидно, что приближенное число 
. Тогда для произведения
. Если пренебречь последним малым слагаемым в скобках, то можно сформулировать следующее правило:
1. Относительная погрешность произведения приближенных чисел равна сумме относительных погрешностей множителей 
.
Так как деление на число b равнозначно умножению на 1/b, то справедливо утверждение:
2. Относительная погрешность частного приближенных чисел равна сумме относительных погрешностей делимого и делителя.
Следовательно, при умножении и делении приближенных чисел необходимо принимать во внимание количество значащих цифр, характеризующих относительную точность числа, а не количество десятичных знаков, обуславливающих его абсолютную погрешность.
|
|
|
Совершенно очевидно, что при большом количестве действий такого сорта правила нельзя считать удовлетворительными, так как погрешности будут иметь разные знаки и компенсировать друг друга. Статистическая оценка показывает, что при N одинаковых действиях среднее значение суммарной ошибки больше единичной в 
раз, если нет систематических причин для накопления погрешности. Систематические причины возникают, если, например в алгоритме вычитаются близкие по величине числа.
|
|
|
