Численные методы поиска минимума функции одной переменной.

Определения.

Функция f (x) имеет локальный минимум при некотором , если существует некоторая конечная ξ-окрестность этого элемента, в которой , . Требуется, чтобы на множестве X функция f (x) была по крайней мере кусочно-непрерывной.

Точка, в которой функция достигает наименьшего на множестве X значения, называется абсолютным минимумом функции. Для нахождения абсолютного минимума требуется найти все локальные минимумы и выбрать наименьшее значение.

Задачу называют детерминированной, если погрешностью вычисления (или экспериментального определения) функции f (x) можно пренебречь. В противном случае задачу называют стохастической. Все изложенные далее методы применимы только к детерминированным задачам.

Методы поиска минимума по нахождению корней уравнений.

Если функция f (x) аналитически дифференцируема, то решаем f ^/(x) = 0 методами, изложенными в предыдущих главах. При этом условие f ^//(x) > 0 в найденной точке указывает нам на минимум. Для использования этих методов необходимо знать либо аналитический вид первой и второй производных, либо рассчитать их численно, если это не приведет к потере точности.

Метод дробления.

Наиболее простой метод поиска минимума. Пусть дана начальная точка x ₀, а также величина и знак шага h, определяющие движение из этой точки в сторону предполагаемого минимума f (x). Метод заключается в последовательном дроблении исходного шага h с изменением его знака при выполнении условия f (x _k+1) > f (x _k), где k – порядковый номер вычисляемой точки. Например, как только очередное значение функции стало больше предыдущего, выполняется h = – h /3 и процесс продолжается до тех пор, пока

| x _k+1 – x _k| ≤ ξ. (1)

Данный метод является одним из самых медленных для поиска минимума. Основное достоинство данного алгоритма – возможность использования в программах управления экспериментальными исследованиями, когда значения функции f(x) последовательно измеряются с шагом h ≥ h _min.

Метод золотого сечения.

Пусть f (x) задана и кусочно-непрерывна на [ x_L, x_R ], и имеет на этом отрезке только один локальный минимум. Золотое сечение, о котором упоминал ещё Евклид, состоит в разбиении интервала [ x_L, x_R ] точкой x ₁ на две части таким образом, что отношение длины всего отрезка к его большей части равно отношению большей части к меньшей:

. (2)

Таким образом, возьмем на отрезке две точки x ₁и x ₂, симметрично относительно границ делящие исходный отрезок в отношении золотого сечения:

,

,

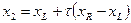где коэффициент .

Если f (x ₁) < f (x ₂), мы должны сузить отрезок справа, т.е. новое значение x _R = x ₂, в противном случае x _L = x ₁. Оставшаяся внутри нового отрезка точка является первым приближением к минимуму и делит этот отрезок в отношении золотого сечения. Таким образом, на каждой итерации приближения к минимуму (см. рисунок) нам нужно ставить только одну точку (x ₁ или x ₂), в которой считать значение функции и сравнивать его с предыдущим. Условием выхода из итерационного процесса будет, подобно предыдущему случаю, условие | x ₂ – x ₁| ≤ ξ.

Метод отличается высокой скоростью сходимости, обычно изысканной компактностью программной реализации и всегда находит точку, минимальную на заданном интервале.

Метод парабол.

Пусть f (x) имеет первую и вторую производную. Разложим f (x) в ряд Тейлора в некоторой точке x _k, ограничиваясь при этом тремя членами разложения:

. (3)

Иными словами, аппроксимируем нашу функцию в точке x _k параболой. Для этой параболы можно аналитически вычислить положение экстремума как корень уравнения первой производной от (3): . Пусть минимум аппроксимирующей параболы находится в точке x _k+1. Тогда вычислив значение функции f (x _k+1), мы получаем новую точку приближения к минимуму.

Обычно в практических реализациях данного метода не используют аналитический вид первой и второй производных f (x). Их заменяют конечно-разностными аппроксимациями. Наиболее часто берут симметричные разности с постоянным шагом h:

;

.

Это эквивалентно аппроксимации функции параболой, проходящей через три близкие точки x _k+ h, x _k, x _k– h. Окончательное выражение, по которому можно строить итерационный процесс, таково:

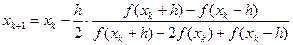. (4)

Данный метод отличается от вышеизложенных высокой скоростью сходимости. Вблизи экстремума, вплоть до расстояний ~ h ², сходимость практически не отличается от квадратичной. Однако алгоритм требует постоянного контроля сходимости. Например, итерационный процесс будет сходиться к минимуму, если

1) знаменатель формулы (4) должен быть >0. Если это не так, нужно сделать шаг в обратном направлении, причем достаточно большой. Обычно в итерационном процессе полагают 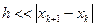. Иногда ради упрощения расчетов полагают , однако это существенно уменьшает скорость сходимости.

2) . Если это не так, то от x _k следует сделать шаг с τ = ½. Если и при этом условие убывания не выполнено, уменьшают τ и вновь делают шаг.

 

⇐ Предыдущая12345678910Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: