 |
Метод Ньютона (касательных).
|
|
|
|
Пусть x 0 – начальное приближение к корню, а f (x) имеет непрерывную производную. Следующее приближение к корню найдем в точке x 1, где касательная к функции f (x), проведенная из точки (x 0, f 0), пересекает ось абсцисс. Затем точно так же обрабатываем точку (x 1, f 1), организуя итерационный процесс. Выход из итерационного процесса по условию 
.
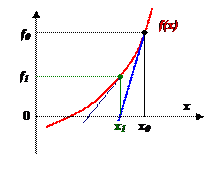Уравнение касательной, проведенной из точки (x 0, f 0): y (x) = f /(x 0)(x – x 0) + f (x 0) дает для y (x 1) = 0 следующее выражение:
, (1)
которое и используется для организации итерационного процесса. Итерации сходятся, только если всюду выполняется условие 
; в противном случае сходимость будет не при любом начальном приближении, а только в некоторой окрестности корня. Итерации будут сходиться к корню с той стороны, с которой 
.
Метод обладает самой высокой скоростью сходимости: погрешность очередного приближения примерно равна квадрату погрешности предыдущего приближения. Метод можно использовать для уточнения корней в области комплексных чисел, что необходимо при решении многих прикладных задач, например при численном моделировании электромагнитных колебательных и волновых процессов с учетом временной и пространственной диссипации энергии.
Недостатком метода можно указать необходимость знать явный вид первой и второй производных, так как их численный расчет приведет к уменьшению скорости сходимости метода. Иногда, ради упрощения расчетов, используют т.н. модифицированный метод Ньютона, в котором значение f /(x) вычисляется только в точке x 0, при этом число итераций увеличивается, но расчеты на каждой итерации упрощаются.
Метод секущих.
В отличие от метода Ньютона, можно заменить производную первой разделенной разностью, найденной по двум последним итерациям, т.е. заменить касательную секущей. При этом первый шаг итерационного процесса запишется так:
|
|
|
.
Для начала итерационного процесса необходимо задать x 0и x 1, которые не обязательно ограничивают интервал, на котором функция должна менять знак; это могут быть любые две точки на кривой. Выход из итерационного процесса по условию .
Сходимость может быть немонотонной даже вблизи корня. При этом вблизи корня может происходить потеря точности, т.н. «разболтка решения», особенно значительная в случае кратных корней. От разболтки страхуются приемом Гарвика: выбирают некоторое ξ x и ведут итерации до выполнения условия 
. Затем продолжают расчет, пока 
убывает. Первое же возрастание может свидетельствовать о начале разболтки, а значит, расчет следует прекратить, а последнюю итерацию не использовать.
Метод простых итераций.
Суть метода простых итераций в принципе совпадает с методом, изложенным для решения систем линейных алгебраических уравнений. Для нелинейного уравнения метод основан на переходе от уравнения
f (x) = 0 (2)
к эквивалентному уравнению x = φ (x). Этот переход можно осуществить разными способами, в зависимости от вида f (x). Например, можно положить
φ (x) = x + bf (x), (3)
где b = const, при этом корни исходного уравнения (2) не изменятся.
Если известно начальное приближение к корню x 0, то новое приближение x 1 = φ (x 0), т.е. общая схема итерационного процесса:
x k+1 = φ (x k). (4)
Наиболее простой критерий окончания процесса 
.
Критерий сходимости метода простых итераций: если вблизи корня | φ /(x)| < 1, то итерации сходятся. Если указанное условие справедливо для любого x, то итерации сходятся при любом начальном приближении. Исследуем выбор константы b в функции (3) с точки зрения обеспечения максимальной скорости сходимости. В соответствии с критерием сходимости наибольшая скорость сходимости обеспечивается при | φ /(x)| = 0. При этом, исходя из (3),
|
|
|
b = –1/ f /(x), и итерационная формула (4) переходит в
,
т.е. в формулу метода Ньютона (1). Таким образом, метод Ньютона является частным случаем метода простых итераций, обеспечивающим самую высокую скорость сходимости из всех возможных вариантов выбора функции φ (x).
|
|
|
