 |
Метод Рунге-Кутты II порядка.
|
|
|
|
Увеличение точности решения ОДУ из предыдущей задачи при заданном шаге h может быть достигнуто учетом большего количества членов разложения функции в ряд Тейлора. Для метода Рунге-Кутты второго порядка следует взять три первых коэффициента, т.е. обеспечить:
. (8)
Переходя к приближенному решению y ≈ u и заменяя производные в (8) конечными разностями, получаем в итоге следующее выражение:
, (9)
где 0 ≤ α ≤ 1– свободный параметр. Можно показать, что если f (x, u) непрерывна и ограничена вместе со своими вторыми производными, то решение, полученное по данной схеме, равномерно сходится к точному решению с погрешностью порядка h 2.
Для параметра α наиболее часто используют следующие значения:
1) 
α = 1. В этом случае
. Графически это уточнение можно интерпретировать так: сначала по схеме ломаных делается шаг h /2, и находится значение 
. В найденной точке определяется наклон касательной к интегральной кривой, который и будет определять приращение функции для целого шага, т.е. отрезок [AB] (см. рисунок) будет параллелен касательной, проведенной в точке (x k + h /2, y (x k + h /2)) к интегральной кривой.
2) α = ½. В этом случае
. Можно представить, что в этом случае по методу Эйлера сначала вычисляется значение функции и наклон касательной к интегральной кривой в точке x k+1. Затем находится среднее положение касательной из сравнения соответствующих наклонов в точках x k и x k+1, которое и будет использоваться для расчета точки y k+1.
Метод Рунге-Кутты IV порядка.
Данная схема является наиболее употребительной. Здесь в разложении функции в ряд Тейлора учитываются члены до h 4 включительно, т.е. погрешность на каждом шаге пропорциональна h 5. Для практических вычислений используются следующие соотношения, обобщенные в данном случае на решение системы ОДУ:
|
|
|
, где i = 1… p, p – число уравнений в системе.
; k – номер точки, для которой осуществляется расчет;
;
;
.
К достоинствам метода следует отнести высокую точность вычислений. Схемы более высокого порядка точности практически не употребляются в силу своей громоздкости. Также немаловажно, что метод является явным, т.е. значение y k+1 вычисляется по ранее найденным значениям за известное заранее число действий.
Все представленные выше схемы допускают расчет с переменным шагом. Например, шаг можно уменьшить там, где функция быстро изменяется, и увеличить в обратном случае. Так, метод Рунге-Кутты-Мерсона позволяет оценивать погрешность на каждом шаге и, в зависимости от полученной оценки принимать решение об изменении шага. Автоматический выбор шага позволяет значительно сократить время вычислений.
Метод Рунге – Кутта - Мерсона.
Этот метод отличается от метода Рунге – Кутта четвертого порядка возможностью оценивать погрешность на каждом шаге и в зависимости от этого принимать решение об изменении шага. Один из вариантов формул:
; 
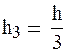
Rn+1 = 0.2k4 – 0.3k3 – 0.1k5 - погрешность на каждом шаге.
Пусть задана максимальна погрешность 
. Если 
, h = h/2, и n+1 цикл расчета повторяется (с точки xn, yn) c новым шагом. Если же
, h = 2h
Автоматический выбор шага позволяет значительно сократить время решения ОДУ.
Схема РКМ обобщается на системы ОДУ аналогично классической схеме Рунге – Кутта.
Метод Адамса.
Метод основан на аппроксимации интерполяционными полиномами правых частей ОДУ.
Пусть с помощью любого из методов, рассмотренных выше, вычислено решение заданного дифференциального уравнения в точках x 1, x 2, x 3 (а в точке x 0 решение и так известно – поставлена задача Коши). Полученные значения функции обозначим как y 0, y 1, y 2, y 3, а значения правой части дифференциального уравнения как f 0, f 1, f 2, f 3, где f k = f (x k, y k). Начиная с четвертой точки, на каждом шаге интегрирования дифференциального уравнения вычисления осуществляются по схеме
|
|
|
P(EC){m}E
где P – прогноз решения; Е – вычисление f(x,y); С – коррекция решения; m – количество итераций коррекции. Схемы такого типа называют «прогноз-коррекция»: это подразумевает сначала приблизительное вычисление решение по формуле низкого порядка, а затем уточнение с учетом полученной информации о поведении интегральной кривой.
Прогноз осуществляется по экстраполяционной формуле Адамса:
. (10)
Коррекция осуществляется по интерполяционной формуле Адамса:
. (11)
Вычисление осуществляется по формуле:
Количество итераций m ≤ p, где p – порядок используемого метода. В ходе каждой итерации решается нелинейное уравнение (11) относительно неизвестной y 4 (обычно методом простых итераций).
Иногда в методе Адамса используется схеме PECE на каждом шаге процесса интегрирования, т.е. осуществляется только одна коррекция. В силу сложности вычислений метод используется только в мощных программных пакетах численного анализа. Формулы метода также легко переносятся на решение систем ОДУ первого порядка.
|
|
|
