 |
Аппроксимация каноническим полиномом.
|
|
|
|
Выберем базисные функции в виде последовательности степеней аргумента x:
φ 0(x) = x 0 = 1; φ 1(x) = x 1 = x; φ m(x) = x m, m < n.
Расширенная матрица Грама для степенного базиса будет выглядеть следующим образом:
.
Особенность вычислений такой матрицы (для уменьшения количества выполняемых действий) состоит в том, что необходимо сосчитать только элементы первой строки и двух последних столбцов: остальные элементы заполняются сдвигом предшествующей строки (за исключением двух последних столбцов) на одну позицию влево. В некоторых языках программирования, где отсутствует быстрая процедура возведения в степень, пригодится алгоритм расчета матрицы Грама, представленный далее.
Выбор базисных функций в виде степеней x не является оптимальным с точки зрения достижения наименьшей погрешности. Это является следствием неортогональности выбранных базисных функций. Свойство ортогональности заключается в том, что для каждого типа полинома существует отрезок [ x 0, x n], на котором обращаются в нуль скалярные произведения полиномов разного порядка:
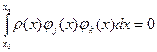, j ≠ k, ρ – некоторая весовая функция.
Если бы базисные функции были ортогональны, то все недиагональные элементы матрицы Грама были бы близки к нулю, что увеличило бы точность вычислений, в противном случае при 
определитель матрицы Грама очень быстро стремится к нулю, т.е. система становится плохо обусловленной.
Блок-схема алгоритма формирования матрицы Грама и аппроксимации полиномом.
Аппроксимация ортогональными классическими полиномами.
Представленные ниже полиномы, относящиеся ко многочленам Якоби, обладают свойством ортогональности в изложенном выше смысле. То есть, для достижения высокой точности вычислений рекомендуется выбирать базисные функции для аппроксимации в виде этих полиномов.
|
|
|
1) Полиномы Чебышева.
Определены и ортогональны на [–1, 1] с весом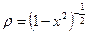 
. В интервал ортогональности всегда можно вписать область определения исходной функции с помощью линейных преобразований.
Строятся следующим образом (рекуррентная формула):
T 0(x) = 1;
T 1(x) = x;
T k+1(x) = 2 xT k(x) – T k–1(x).
2) Полиномы Лежандра.
Определены и ортогональны на [–1, 1] с весом 
.
Строятся следующим образом (рекуррентная формула):
L 0(x) = 1;
L 1(x) = x;
.
Сглаживание и линейная регрессия.
Рассмотрим несколько наиболее простых с точки зрения программной реализации случаев аппроксимации (сглаживания).
1) Линейная регрессия.
В случае линейного варианта МНК (линейная регрессия) φ (x) = a + bx можно сразу получить значения коэффициентов a и b по следующим формулам:
,
,
где 
, 
.
2) Линейное сглаживание по трём точкам.
3) Линейное сглаживание по пяти точкам.
Решение нелинейных уравнений с одним неизвестным.
Общие сведения о численном решении уравнений с одним неизвестным.
Пусть задана непрерывная функция f (x). Требуется найти корни уравнения f (x) = 0 численными методами – это и является постановкой задачи. Численное решение уравнения распадается на несколько подзадач:
1) Анализ количества, характера и расположения корней (обычно путем построения графика функции или исходя из физического смысла исследуемой модели). Здесь возможны следующие варианты:
- единственный корень;
- бесконечное множество решений;
- корней нет;
- имеется несколько решений, как действительных, так и мнимых (например, для полинома степени n). Корни четной кратности выявить сложно.
2) Локализация корней (разбиение на интервалы) и выбор начального приближения к каждому корню. В простейшем случае можно протабулировать функцию с заданным шагом.
|
|
|
|
|
|
