T – критерий Стьюдента для независимых выборок

t = ,

где х₁ - среднее арифметическое значение 1-й выборки;

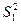- дисперсия 1-й выборки;

n₁ – объем первой выборки (количество индивидуальных значений в первой выборке);

число степеней свободы: n = n₁ + n₂ – 2

 

t – критерий Стьюдентадля зависимых выборок

t = ,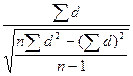

 

где d – разность между результатами в каждой паре (d=х_после-х_до);

n – число пар данных (объем выборки).

число степеней свободы: n = n – 1

или

,

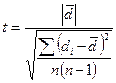где - среднее значение сдвигов.

Оценка достоверности различий выборочной средней
и генеральной средней

В некоторых случаях значение генеральной средней известно, например оно может быть получено в процессе стандартизации психодиагностического теста с помощью весьма большой по объему, в несколько тысяч испытуемых, выборки стандартизации. Для этой цели используется формула:

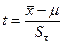
Где - ошибка репрезентативности для генерального среднего;

- выборочное среднее;

μ – генеральное среднее;

ошибка репрезентативности

n - объем выборки;

число степеней свободы n = n – 1,

Например, в тесте Векслера, измеряющем уровень умственного развития, среднее значение генерального среднего 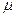=100.

 

F- критерий Фишера

Назначение. Определение достоверности или недостоверности различия двух выборочных дисперсий в сравниваемых выборках.

Критерий Фишера позволяет сравнивать величины выборочных дисперсий двух рядов наблюдений. Для вычисления F_эмп нужно найти отношение дисперсий двух выборок, причем так, чтобы большая по величине дисперсия находилась бы в числителе, а меньшая – в знаменателе.

df₁ – число степеней свободы, df₁ = n₁ -1

n₁ – объем первой выборки ().

df₂ – число степеней свободы, df₂ = n₂ -1

n₂ – объем второй выборки ().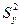

Если выборки взяты из одной генеральной совокупности или из разных совокупностей с одинаковыми генеральными дисперсиями, то подтверждается нулевая гипотеза.

 

Примеры решения задач

Критерий Стьюдента для независимых выборок.

Задача. Рассмотрим задачу раздела 4, которая ранее была решена по критерию Манна-Уитни.

Исследование социального интеллекта студентов специальности информатика проводилось по тесту Гилфорда-Салливена. Достоверно ли различие между средними значениями показателей социального интеллекта студентов первого и четвертого курса. Результаты исследования социального интеллекта (SQ) у студентов первого курса: 35, 18, 26, 29, 33, 31, 25, 27, 31, 33. Результаты исследования социального интеллекта (SQ) у студентов четвертого курса: 29, 33, 31, 30, 36, 31, 35, 28, 26, 30, 38.

Решение.

Решение задачи при помощи критерия Стьюдента для независимых выборок.

Гипотезы:

Н₀: Среднее значение социального интеллекта студентов четвертого курса не выше среднего значения социального интеллекта студентов первого курса

Н₁: Среднее значение социального интеллекта студентов четвертого курса выше среднего значения социального интеллекта студентов первого курса

 

Эмпирическое значение критерия вычисляется по формуле:

,

где, 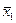и - средние арифметические значения для первой и второй выборок соответственно;

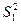и - дисперсии первой и второй выборок соответственно;

n₁ и n₂ – объем первой выборки (количество индивидуальных значений в первой выборке) и второй выборки;

Среднее арифметическое значение вычислим по формуле:

 

В исследовании приняло участие 10 студентов первого курса (n₁=10) и одиннадцать студентов четвертого курса (n₂=11). Среднее арифметическое значение социального интеллекта у студентов первого курса 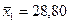, у студентов четвертого курса .

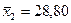Так как, n<30, выборочную дисперсию вычислим по формуле:

Дисперсия для первой выборки (студенты первого курса), , дисперсия для второй выборки (студенты второго курса), .

Вычислим эмпирическое значение критерия

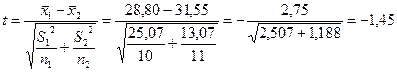
Число степеней свободы: n = n₁ + n₂ – 2 = 10 + 11 – 2 = 19

По таблице Приложения определим критические значения. Для уровня статистической значимости р=0,05 критическое значение критерия t_0,05=2,09, для уровня статистической значимости р=0,01 критическое значение критерия t_0,01= 2,86.

На этапе принятия решения рассматривается абсолютная величина эмпирического критерия, то есть знак не учитывается. Т_эмп=1,45.

Сопоставив значения, мы можем заключить, что р_эмп>0,05, следовательно, мы не можем отклонить нулевую гипотезу.

Результаты исследования представим наглядно.

 

 

Статистический вывод: так как уровень статистической значимости эмпирического значения критерия р_эмп>0,05, мы принимаем нулевую гипотезу - Н₀.

Психологический вывод: Социальный интеллект студентов четвертого курса не выше социального интеллекта первого курса.

 

⇐ Предыдущая234567891011Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: