 |
Н – критерий Крускала-Уоллиса
|
|
|
|
Критерий применяется для оценки различий по степени выраженности исследуемого признака, если выборок три и более.
Составляются ненаправленные гипотезы.
Эмпирическое значение критерия вычисляется по формуле:

где N - общее количество испытуемых в объединенной выборке;
nj - количество испытуемых в j -ой группе;
Tj - суммы рангов в j -ой группе;
k – количество выборок (групп).

Алгоритм вычисления Нэмп подобен алгоритму критерия Манна-Уитни. Ранжирование осуществляется по единой выборке, составленной из первичных данных всех групп.
При количестве групп с>3 или количестве испытуемых n1,n2,n3>5, критические значения определяются по таблице для критерия χ2-Пирсона. Число степеней свободы определяется по формуле: ν=с-1. Где с -количество выборок.
S – критерий Джонкира
Критерий предназначен для выявления тенденций изменения признака при сопоставлении от трех до шести выборок.
Выборки должны быть одинаковы по объему и упорядочены в порядке возрастания среднего значения признака. Если число данных в каждой выборке различно, то следует случайным образом уравнять выборки. Количество элементов в каждой выборке не менее двух и не более 10.
Составляются направленные гипотезы.
Эмпирическое значение критерия вычисляется по формуле:
Sэмп=2A-B
Сумма инверсий определяется по формуле: А =  ,
,
где, Si -равно количеству значений справа, превышающих i–е значение по величине.
В - максимально возможное количество превышающих значений, которое мы получили бы, если бы все значения справа были выше значений слева:

с - количество столбцов (сопоставляемых групп);
n - количество наблюдений в каждом столбце (группе).
|
|
|
Примеры решения задач
Критерий Манна-Уитни
Используя тестГилфорда-Салливена исследователь определил показатели социального интеллекта у двух групп студентов. В исследовании приняли участие десять студентов первого курса и одиннадцать студентов четвертого курса специальности информатика. Результаты исследования социального интеллекта (SQ) у студентов первого курса: 35, 18, 26, 29, 33, 31, 25, 27, 31, 33. Результаты исследования социального интеллекта (SQ) у студентов четвертого курса: 29, 33, 31, 30, 36, 31, 35, 28, 26, 30, 38.
Определить достоверно ли различие по уровню социального интеллекта между студентами первого и четвертого курса.
Решение.
Для решения выбираем критерий Манна-Уитни.
Гипотезы:
Н0: Социальный интеллект студентов четвертого курса не выше социального интеллекта студентов первого курса
Н1: Социальный интеллект студентов четвертого курса выше социального интеллекта студентов первого курса
Эмпирическое значение критерия вычисляется по формуле:

где n1 - количество испытуемых в первой выборке;
n2 - количество испытуемых во второй выборке;
Tx – большая из двух ранговых сумм;
nx – количество испытуемых в группе с большей суммой рангов.
По условию задачи, в исследовании приняло участие 10 студентов первого курса (n1=10) и одиннадцать студентов четвертого курса (n2=11).
Для определения Tx переводим индивидуальные значения социального интеллекта в ранговые. Для этого из данных двух выборок составляем единый вариационный ряд, который содержит 21 значение (n1+ n2=10+11=21). Данные этого ряда ранжируем. Правило ранжирования представлено в разделе «измерение в психологии».
Результаты ранжирования представлены в таблице.
Результаты ранжирования
| № п/п | SQ (социальный интеллект) | ранг |
| 3,5 | ||
| 3,5 | ||
| 7,5 | ||
| 7,5 | ||
| 9,5 | ||
| 9,5 | ||
| 12,5 | ||
| 12,5 | ||
| 12,5 | ||
| 12,5 | ||
| 18,5 | ||
| 18,5 | ||
| Сумма рангов |
|
|
|
Проверим правильность ранжирования. В ранжируемом вариационном ряду 21 значение, N=21. Общая сумма рангов равна 231.
По формуле для проверки правильности ранжирования она также равна 231.
 =
=  = 231
= 231
Суммы рангов, полученные путем сложения и рассчитанные по формуле, совпадают. Следовательно, ранги проставлены правильно.
Ранги записываются в исходной таблице рядом с индивидуальными значениями.
Подсчитывается сумма рангов для каждой группы: T1 и T2.
| № п/п | Студенты 1 курса | Студенты 4 курса | ||
| социальный интеллект, SQ | Ранг, R | социальный интеллект, SQ | Ранг, R | |
| 18,5 | 7,5 | |||
| 3,5 | 12,5 | |||
| 7,5 | 9,5 | |||
| 12,5 | 12,5 | |||
| 18,5 | ||||
| 12,5 | 3,5 | |||
| 9,5 | ||||
| Сумма рангов | 94,5 | 136,5 |
Сумма рангов по выборке студентов первого курса Т1=94,5. Сумма рангов по выборке студентов четвертого курса Т2=136,5.
Общая сумма рангов Т1+Т2=94,5+136,5=231 совпадает с расчетной.
Из этих двух сумм определяется большая, ей присваивается обозначение – Тх. Большая сумма рангов у студентов четвертого курса, поэтому Тх=136,5. Так как, nx – количество испытуемых в группе с большей суммой рангов, nx=11.
Рассчитаем эмпирическое значение критерия.

По таблице Приложения определим критические значения. Для уровня статистической значимости р=0,05 критическое значение критерия U0,05=31, для уровня статистической значимости р=0,01 критическое значение критерия U0,01= 22.
Результаты исследования представим наглядно.

Статистический вывод: так как рэмп>0,05 мы принимаем нулевую гипотезу - Н0.
Психологический вывод: социальный интеллект студентов четвертого курса не выше социального интеллекта студентов первого курса.
Задания для самостоятельной работы
№ 4.1. Определялся уровень субъективного контроля учеников одиннадцатых классов. В исследовании приняло участие 12 учеников гимназического класса и 13 учеников обычного класса. Можно ли утверждать, что уровень субъективного контроля у учащихся гимназического и обычного класса различен?
|
|
|
Гимназический класс: 20, 19, 27, 20, 25, 21, 19, 13, 15, 13, 22, 26.
Обычный класс: 15, 25, 25, 19, 29, 28, 23, 25, 28, 26, 16, 30, 30.
№ 4.2. В марте определялся уровень астенического состояния студентов медицинского училища. В исследовании принимали участие студенты первого и третьего курса (возраст от 17 до 21 года). В исследовании приняло участие 14 студентов первого курса и 12 студентов третьего курса. Можно ли утверждать, что астеническое состояние студентов первого курса превосходит астеническое состояние студентов третьего курса?
Показатели астенического состояния студентов первого курса: 61, 51, 52, 45, 43, 74, 47, 48, 50, 52, 57, 56, 68, 43.
Показатели астенического состояния студентов третьего курса: 63, 57, 64, 67, 44, 50, 42, 45, 40, 42, 45, 63.
№ 4.3. Уровень общей тревожности определялся у учеников седьмого класса средней школы в марте. Результаты исследования представлены в таблице.
| № п/п | Мальчики | Девочки | Различаются ли мальчики и девочки по уровню общей тревожности? |
№ 4.4. Можно ли утверждать, что уровень вербальной агрессии учеников девятого класса превосходит уровень вербальной агрессии учеников одиннадцатого класса? Уровень вербальной агрессии определялся по тесту Басса-Дарки.
| Код ученика | 9-й класс | 11-й класс |
№ 4.5. С целью определения уровня развития интеллектуальных процессов в младшем школьном возрасте, проведено тестирование школьников второго и третьего классов. В исследовании приняло участие 13 учеников второго класса и 14 учеников третьего класса. Можно ли утверждать, что уровень развития интеллектуальных процессов учеников третьего класса превосходит уровень развития интеллектуальных процессов учеников второго класса? Результаты исследования представлены в таблице.
|
|
|
| 2-й класс | ||||||||||||||
| 3-й класс |
№ 4.6. Школьная готовность двух подготовительных групп детского сада определялась по тесту Керна-Йерасека. Объем первой выборки – 14 детей, второй – 11 детей. Различаются ли эти две группы по уровню готовности к обучению в школе? Результаты исследования представлены в таблице.
| Группа 1 | ||||||||||||||
| Группа 2 |
№ 4.7. Для определения объема кратковременной зрительной памяти студентам был предложен ряд из двенадцати двузначных цифр для запоминания. В исследовании участвовали студенты первого курса техникума. Индивидуальные значения для студентов «экономистов» и «электриков» представлены в таблице. Можно ли утверждать, что уровень кратковременной зрительной памяти в одной из групп выше, чем в другой?
| Код студента | экономисты | электрики |
№ 4.8. С помощью теста Векслера исследовался уровень образного мышления детей посещающих детский сад. Дошкольникам предъявлялось 14 картинок. За каждый правильный ответ начислялся 1 балл. В таблице представлены полученные результаты. Можно ли утверждать, что одна из групп превосходит другую по уровню образного мышления?
| № п/п | 5-6 лет | 6-7 лет |
№ 4.9. По методике Айзенка был определен показатель нейротизма подростков 14-15 лет. Показатели нейротизма в группах:
Девочки: 16, 14, 18, 11, 11, 19, 12, 11, 13, 16, 9, 13
Мальчики: 12, 10, 19, 15, 4, 9, 7, 11, 14, 5, 11, 9, 16
Можно ли утверждать, что в подростковом возрасте нейротизм мальчиков превосходит нейротизм девочек?
№ 4.10. Определялся уровень развития психических процессов у учащихся одиннадцатых классов - гимназического и обычного – по методике «Опросник для выявления общих способностей для учащихся 8-11 классов» (модификация В.Ф.Сафина).
|
|
|
Гимназический класс
| Инициалы | Общая активность (А) | Эмоциональность (Э) | Образная память (П) | Воображение (Во) | Саморегуляция (С) | Воля (В) | Аналитическое мышление (М) | Уровень развития психических процессов |
| Е.О. | ||||||||
| Ш.Е. | ||||||||
| А.А. | ||||||||
| М.И. | ||||||||
| Р.Г. | ||||||||
| Б.И. | ||||||||
| Ф.И. | ||||||||
| С.И | ||||||||
| См.И | ||||||||
| Л.Т |
Обычный класс
| Инициалы | Общая активность (А) | Эмоциональность (Э) | Образная память (П) | Воображение (Во) | Саморегуляция (С) | Воля (В) | Аналитическое мышление (М) | Уровень развития психических процессов |
| К.О. | ||||||||
| С.Л. | ||||||||
| Х.С. | ||||||||
| М.Р. | ||||||||
| И.Л. | ||||||||
| П.Н. | ||||||||
| М.А. | ||||||||
| Б.И. | ||||||||
| Н.И. | ||||||||
| П.А. | ||||||||
| В.Н. | ||||||||
| М.В |
Можно ли утверждать, что уровень развития психических процессов в гимназическом классе выше, чем в обычном?
№ 4.11. В дипломном исследовании Л.И.Киселева изучала взаимосвязь уровня самооценки и характеристик затрудненного общения. Выборку составили студенты индустриального колледжа в возрасте 16 лет. В таблице представлены сводные результаты по методике исследования самооценки личности и опроснику «Социально-психологические характеристики субъекта общения», для шкал ЭР (экспрессивно-речевые особенности) и СП (социально-перцептивные особенности). Более высокие значения по этим шкалам соответствуют более высокой оценке степени затруднений, которые испытывает субъект во взаимодействии.
| № участника | заниженная самооценка | адекватная самооценка | завышенная самооценка | |||
| ЭР | СП | ЭР | СП | ЭР | СП | |
| 6,5 8,1 8,6 11,9 | 5,9 11,6 8,1 8,6 | 10,3 7,0 7,6 7,8 | 7,3 7,6 6,7 6,8 | 7,3 8,4 11,6 10,3 7,8 8,4 6,7 9,4 | 7,0 8,4 9,2 8,1 9,9 10,5 7,3 11,3 | |
| среднее | 8,8 | 8,6 | 8,2 | 7,1 | 8,7 | 8,5 |
Построить графики, отражающие значение показателей «экспрессивно-речевые особенности» и «социально-перцептивные особенности» у студентов с разной самооценкой.
Определить, достоверно ли, что люди с адекватной самооценкой испытывают субъективно меньше затруднений во взаимодействии, чем люди с неадекватной самооценкой.
№ 4.12. Среди учеников 6, 8, 9, 10-х классов средней школы методом тестирования определялся уровень общительности.
Можно ли утверждать, что общительность в старших классах выше, чем в младших.
| Код учащегося | 6 класс | 8 класс | 9 класс | 10 класс |
№ 4.13. Решить задачу, обосновав выбор статистического критерия.
Для случайной выборки из 5 учеников каждой школы в таблице представлены результаты контрольного задания, содержащего 10 задач. Одинакова ли подготовленность по заданному предмету учеников пятых классов трех различных школ?
| Номер школы | |||
| №1 | №2 | №3 | |
| Результаты учеников | |||
5. ОЦЕНКА ДОСТОВЕРНОСТИ СДВИГА
В ЗНАЧЕНИЯХ ИССЛЕДУЕМОГО ПРИЗНАКА
Критерии, представленные в данном разделе предназначены для работы с зависимыми выборками.
Выборки называются зависимыми (связными), если процедура эксперимента и полученные результаты измерения некоторого свойства, проведенного на одной выборке, оказывают влияние на другую.
Примером зависимых выборок является группа, на которой дважды проводилось психологическое обследование (или группа в условиях «до» и «после» воздействия).
Типичные сдвиги - сдвиги, которые нам кажутся преобладающими.
Нетипичные сдвиги – сдвиги более редкого, противоположного направления.
G – критерий знаков
Критерий часто применяется для решения задачи выявления изменения признака. Применяется, если в исследовании два замера (чаще условие «до-после»).
Составляются ненаправленные гипотезы.
Алгоритм. Определить для каждой пары значений направление сдвига d=хпосле-хдо. Подсчитать количество «положительных» (G+) и «отрицательных» (G-) сдвигов. Считать меньшее из двух вычисленных значений нетипичным, Gнетип.. Считать Gэмп= Gнетип. Сопоставить Gэмп с Gкр(n). Где n – общее количество сдвигов. При наличии нулевых сдвигов, общее количество сдвигов (n) меньше объема выборки.
Т – критерий Вилкоксона
Критерий применяется для решения задачи выявления изменения признака количественно измеренного. Применяется, если в исследовании два замера (чаще условие «до-после»). Данный критерий более мощный, чем критерий знаков, так как учитывает не только направление сдвига, но и его выраженность.
Для данного критерия составляются направленные гипотезы.
Эмпирическое значение критерия вычисляется по формуле:


где R-ранги, нетипичного направления сдвига
Алгоритм. 1)Определить для каждой пары значений направление и значение сдвига d=xпосле-хдо. 2) Проранжировать ряд, полученный из абсолютных значений сдвигов (знак сдвига не учитывается, нулевой сдвиг не ранжируется).
3) Подсчитать суммы рангов: T+ =  и T- =
и T- = 
где R+ – ранговые значения сдвигов с положительным знаком.
R- – ранговые значения сдвигов с отрицательным знаком.
4. Считать меньшую из двух ранговых сумм эмпирическим значением критерия (Tэмп). 5.Сопоставить Tэмп с Tкр(n). Где n – общее количество сдвигов. При наличии нулевых сдвигов, общее количество сдвигов (n) меньше объема выборки.
Критерий  Фридмана
Фридмана
Критерий можно рассматривать как распространение критерия Вилкоксона на три и большее количество значений признака связной выборки испытуемых. Критерий не позволяет выявить направление изменений, позволяет лишь установить достоверность различий признака в разных условиях.
Составляются ненаправленные гипотезы.
Эмпирическое значение критерия рассчитывается по формуле:
 =
= 
При этом, 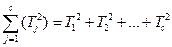
где с – количество условий;
n – объем выборки;
Tj – сумма рангов по j-му условию.
Ранжирование осуществляется по строкам, т.е. ранжируются индивидуальные значения испытуемого, полученные в разных условиях.
При общем количестве измерений с=3 и числе испытуемых от 2 до 9 критические значения определяются по таблице Приложения для критерия Фридмана. При общем количестве измерений с=4 и числе испытуемых от 2 до 4 критические значения определяются по таблице Приложения для критерия Фридмана.
При большем количестве измерений и/или испытуемых критические значения определяются по таблице для критерия χ2-Пирсона. Число степеней свободы определяется по формуле ν=с-1.
L – критерий Пейджа
Критерий применяется для сопоставления показателей измеренных в трех и более условиях на одной и той же выборке испытуемых.
Критерий позволяет выявить тенденции в изменении величин признака при переходе от условия к условию. Он не только констатирует различия, но и указывает на направление изменений.
Применим когда n≤12 (объем выборки) и количество замеров с≤6.
Составляются направленные гипотезы.
Ранжирование осуществляется по строкам, т.е. ранжируются индивидуальные значения участника исследования, полученные в разных условиях (по строке).
Эмпирическое значение критерия рассчитывается по формуле:
Lэмп =  ,
,
где, Тj – сумма рангов по данному условию.
j – порядковый номер, приписанный данному условию в упорядоченной последовательности условий.
Выборки (условия) должны быть упорядочены в соответствии с суммой рангов по выборке. Выборке с меньшей ранговой суммой присваивается значение j=1.
Тест МакНемара
(данные представлены в дихотомической шкале)

Значения A и D определяются из таблицы сопряженности
| после | |||
| - | + | ||
| до | + | А | В |
| - | С | D |
где A – количество человек имеющих: до «+» и «-» после;
B – количество человек имеющих: до «+» и «+» после;
C - количество человек имеющих: до «-» и «-» после;
D - количество человек имеющих: до «-» и «+» после;
По категории «до» - плюс обозначает проявление изучаемого показателя, или его высокое значение; минус – отсутствие проявления изучаемого показателя или его низкое значение. По категории «после» - «плюс» обозначает увеличение изучаемого показателя, «минус» – отсутствие изменения или уменьшение изучаемого показателя.
Примеры решения задач
Задача. Исследование социального интеллекта студентов специальности информатика проводилось по тесту Гилфорда-Салливена. Достоверно ли изменение социального интеллекта у студентов четвертого курса вследствие проведения тренинга коммуникативной компетентности? В таблице приведены результаты измерения.
| № п/п | Значение социального интеллекта до тренинга | Значение социального интеллекта после тренинга | Сдвиг |
| +2 | |||
| +6 | |||
| +3 | |||
| -3 | |||
| +1 | |||
| +4 | |||
| -2 | |||
| +3 | |||
| +4 | |||
| +1 | |||
| +5 | |||
| -1 | |||
| +6 |
Вариант 1. Для решения выбираем G-критерий знаков.
Гипотезы:
Н0: Тренинг коммуникативной компетентности не повлиял на значение социального интеллекта студентов
Н1: Тренинг коммуникативной компетентности повлиял на значение социального интеллекта студентов
Для каждой пары значений определить направление сдвига d = хпосле - хдо. Значение записать в таблицу.
Подсчитать количество положительных и отрицательных сдвигов. Количество «положительных» сдвигов десять, G+=10; количество «отрицательных» сдвигов три, G-=3.
Меньшее из двух значений считается нетипичным сдвигом (Gнетип.), поэтому Gнетип.=3.
Считать Gэмп= Gнетип=3.
Для принятия решения - выбора гипотезы - необходимо сопоставить Gэмп с Gкр(n), где n – общее количество сдвигов.
Общее количество сдвигов n=13, так как положительных сдвигов десять, отрицательных сдвигов три, нулевые сдвиги не учитываются.
По таблице определяем критические значения критерия при данном количестве сдвигов.
Для уровня статистической значимости р=0,05 критическое значение критерия G0,05=3, для уровня статистической значимости р=0,01 критическое значение критерия G0,01=1.
Результаты вычисления представим наглядно.
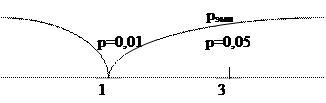
Статистический вывод: так как рэмп=0,05 нулевая гипотеза Н0 отклоняется и принимается альтернативная гипотеза на уровне статистической значимости р=0,05.
Психологический вывод: тренинг коммуникативной компетентности повлиял на социальный интеллект студентов (р=0,05).
Вариант 2. Для решения выбираем T-критерий Вилкоксона.
Гипотезы:
Н0: Показатель социального интеллекта после тренинга коммуникативной компетентности не выше, чем до тренинга
Н1: Показатель социального интеллекта после тренинга коммуникативной компетентности выше, чем до тренинга
Для каждой пары значений определить направление и значение сдвига d=xпосле-хдо. Результат вычисления записывается в таблицу.
В соседний столбик записываются абсолютные значения сдвигов, то есть, знак не учитывается.
Полученный ряд ранжируется, при этом нулевой сдвиг не ранжируется.
Ранг числа записывается в следующий столбик
| № п/п | Значение социального интеллекта до тренинга | Значение социального интеллекта после тренинга | Сдвиг, d | Абсолютные величины сдвига | Ранги абсолютных величин разностей |
| +2 | 4,5 | ||||
| +6 | 12,5 | ||||
| +3 | |||||
| -3 | |||||
| +1 | |||||
| - | |||||
| +4 | 9,5 | ||||
| -2 | 4,5 | ||||
| +3 | |||||
| +4 | 9,5 | ||||
| +1 | |||||
| +5 | |||||
| -1 | |||||
| - | |||||
| +6 | 12,5 | ||||
| сумма |
Проверим правильность ранжирования.
Сложим все ранги и подсчитаем сумму рангов: 4,5+12,5+7+7+2+9,5+4,5+7+9,5+2+11+2+12,5=91.
Подсчитаем сумму рангов по формуле:
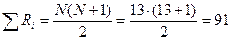
Обе величины совпали, 91=91, следовательно, ранжирование проведено правильно.
Ориентируясь на знак сдвига, подсчитать суммы рангов соответствующие положительному направлению сдвигов T+ =  и отрицательному направлению сдвигов T- =
и отрицательному направлению сдвигов T- =  .
.
Где R+ – ранговые значения сдвигов с положительным знаком;
R- – ранговые значения сдвигов с отрицательным знаком.
T+ =  =4,5+12+7+2+9,5+7+9,5+2+12+4,5=77,5
=4,5+12+7+2+9,5+7+9,5+2+12+4,5=77,5
T- =  =7+4,5+2=13,5
=7+4,5+2=13,5
Эмпирическое значение критерия (Tэмп) соответствует меньшей из двух ранговых сумм, следовательно Tэмп=13,5.
Общее количество сдвигов n=13, так как десять положительных сдвигов и три отрицательных сдвига.
По таблице определяем критические значения критерия при данном количестве сдвигов. Для уровня статистической значимости р=0,05 критическое значение критерия Т0,05=21, для уровня статистической значимости р=0,01 критическое значение критерия Т0,01=12.
Результаты вычисления представим наглядно.

Статистический вывод: так как рэмп<0,05, нулевая гипотеза Н0 отклоняется и принимается альтернативная гипотеза на уровне статистической значимости р<0,05.
Психологический вывод: тренинг коммуникативной компетентности способствовал развитию социального интеллекта студентов (р<0,05).
|
|
|


