Продолжительность жизни, таблицы и кривые выживания

 

Как это ни парадоксально, но разговор о росте численности популяции проще начинать с анализа смертности, в частности с рассмотрения того, как смертность в тех или иных популяциях распределяется по возрастам.

 

Продолжительность жизни

 

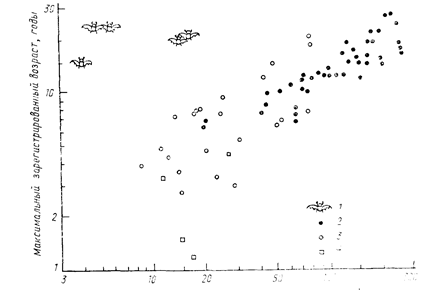Для каждого вида организмов существует некоторая максимальная возможная продолжительность жизни. В природе до возраста, близкого к максимальному, доживает ничтожно малая доля особей, и поэтому при анализе динамики природных популяций величина максимальной продолжительности жизни представляет интерес только как крайняя точка отсчета при построении кривых и таблиц выживания (подробнее об этом ниже). По существующим оценкам максимальная продолжительность жизни варьируется очень широко: от десятков минут у бактерий[21], находящихся в оптимальных лабораторных условиях, до нескольких тысячелетий у некоторых видов древесных растении (таковы, например, произрастающие в западной части Северной Америки секвойя Sequoiadendron giganteum и сосна Pinus longaeva или росшее до 1868 г. на острове Тенериф «драконово дерево» Dracaena draco). Таким образом, диапазон известных значений максимальной продолжительности жизни изменяется в пределах девяти порядков—от 10³ до 10¹¹ с. Обычно продолжительность жизни крупных животных и растений существенно больше, чем мелких, но из этого правила в пределах самых разных групп организмов встречаются и исключения. На рис. 17 показано соотношение размеров тела и максимальной зарегистрированной продолжительности жизни для различных представителей млекопитающих. Как видно из приведенного рисунка, указанная зависимость в целом проявляется, но рукокрылые из нее выпадают, так как в сравнении с другими мелкими млекопитающими могут жить довольно долго.

Продолжительность жизни организмов одного вида может сильно изменяться в зависимости от условий существования. Так, например, пойкилотермные животные, как правило, живут дольше при низкой температуре, чем при высокой (конечно, в том случае, если температуры эти не выходят за пределы толерантности). Для некоторых беспозвоночных, например ветвистоусых рачков дафний, известна зависимость максимальной продолжительности жизни от условий питания: при поддержании в эксперименте постоянной высокой концентрации пищи продолжительность жизни дафнии меньше, чем при умеренном кормлении, но больше, чем в условиях крайне низкой концентрации пищи, когда животные испытывают сильное голодание (Lynch, Ennis, 1983). Причины такого снижения не очень понятны, но не исключено, что оно связано с усилением функции размножения: укорачивание жизни есть «плата» за более интенсивное размножение.

 

Таблицы выживания

 

Средняя продолжительность жизни в сравнении с максимальной кажется показателем более информативным для эколога, но и эта величина сама по себе не может заменить сведений о характере распределения смертности по возрастам, сведений, которые обычно представляют в форме таблиц выживания[22]. Попытка составить таблицы была предпринята одним из основателей демографии — английским исследователем Джоном Грантом (1620—1674). Исходным материалом для расчетов Гранта служили данные по смертности жителей Лондона, собранные в церковных приходах с сугубо практической целью — сообщать о начале эпидемий чумы. Динамика численности населения Лондона в то время определялась в значительной степени миграциями из сельской местности, и поэтому полученные Грантом данные оказались трудными для интерпретации. Первая таблица выживания, похожая на современные, была составлена в 1693 г. английским астрономом Э. Галлеем (известным широкой публике по имени описанной им кометы) для города Бреслау (ныне Вроцлав на территории Польши), численность населения в котором сохранялась стационарной.

В ряде случаев самый простой способ построения таблиц выживания — это подробное наблюдение за судьбой когорты, т. е. большой группы особей, отрожденных в популяции за короткий (относительно общей продолжительности жизни изучаемых организмов) промежуток времени, и регистрация возраста наступления смерти всех членов данной когорты. В первой графе демографической таблицы указывают возраст (точнее, возрастные интервалы, или «классы»), во второй—число доживших до этого возраста особей. В последующих графах—значения таких (вычисленных по данным первых двух граф) параметров, как доля особей, доживших до определенного возраста, удельная смертность в пределах каждого возрастного класса и ожидаемая для каждого возраста средняя продолжительность жизни (табл. 1). Полный вариант таблицы выживания содержит также сведения о распределении рождаемости по возрастам (об этом речь пойдет дальше).

 

Возраст, годы, х	Число живых особей в момент учета, nx	Доля особей, доживших до начала возрастного интервала х, lx	Число особей, погибших от начала интервала х до начала интервала х + 1, dx	Смертность в интервале х, qx	Ожидаемая продолжительность жизни особей, доживших до начала интервала х, ex

 

Начальный, или «нулевой», возраст выбирается достаточно условно в зависимости от объектов и конкретных задач того или иного исследования. Так, например, изучая птиц, можно за «нулевой» возраст принять момент откладки яиц, но можно и момент вылупления птенцов или даже момент вылета их из гнезда. Размер начальной выборки, т. е. того реального числа особей «нулевого возраста», за дальнейшей судьбой которых будут вестись наблюдения, стараются сделать по возможности большим. Так, в демографии фигурируют обычно выборки в 10000 и даже в 100000 особей, в экологии—чаще всего в 1000 особей, хотя, конечно, бывают случаи, когда исследователям приходится довольствоваться выборками в 100 особей. Численность когорты по определению со временем может только снижаться. Соответственно по мере увеличения возраста когорты должна снижаться и доля особей, доживших до данного возраста.

Выделение возрастных классов производят в зависимости от длительности жизни изучаемых организмов, а также особенностей их жизненного цикла. Так, например, для человека выбирают интервалы по 5 лет, для мелких грызунов это могут быть интервалы по одному или несколько месяцев, для многих насекомых—около недели. В ряде случаев при разбивке всего жизненного цикла на отдельные возраста опираются не столько на «астрономический» возраст (измеряемый сутками, месяцами или годами), сколько на возраст «физиологический», определяемый достижением той или иной стадии развития. Так, например, у насекомых мы можем различить стадию яйца, личинки (во многих случаях также разных личиночных возрастов, отделяемых линьками), куколки (у характеризующихся полным превращением) и взрослого организма (имаго).

В качестве примера построения таблицы выживания рассмотрим данные Дж. Коннела (Connel, 1970), наблюдавшего в течение нескольких лет за когортой усоногого ракообразного Balanus glandula в приливно-отливной зоне одного из островов у северо-западного побережья США. Свои наблюдения Коннел начал в 1959 г., спустя примерно 1—2 месяца после того, как произошло оседание личинок, а закончил в 1968 г., когда погибли последние особи из выбранной когорты. В первой графе указан возраст х (в данном случае возрастной интервал соответствует одному году), во второй—число особей п_х, доживших до начала интервала х; в третьей l_х— доля организмов, доживших до возраста х; в четвертой d_x — число особей, погибших в течение интервала х до момента х + 1; в пятой q_x— смертность в течение интервала x; в шестой e_x— ожидаемая продолжительность жизни организмов, доживших до начала возрастного интервала х. По определению n_x+1 = n_x – d_x; q_х = d_x/n_x; l_x = n_x/n₀ где п₀ — число особей начального, «нулевого», возраста. Чтобы рассчитать ожидаемую продолжительность жизни, необходимо сначала узнать среднее число особей, которые были живыми в течение интервала между возрастом х и возрастом x + 1. Эта величина L_x определяется как L_х = (n_x + n_x+1)/2. Сумма значений L_x от конца таблицы до какого-то определенного возраста x, т. е. — это промежуточная величина (размерность ее—«особи×возраст»), необходимая для расчета средней ожидаемой продолжительности жизни e_х особей возраста х. Данная величина рассчитывается, как e_x = T_x/n_x. В табл. 2 приведены значения вспомогательных величин L_x и T_x, для обсуждаемого выше примера с балянусами. Если, например, нам надо рассчитать значение ожидаемой продолжительности жизни балянусов, достигших двухлетнего возраста, мы должны сначала найти величину L_x для этого и последующего возрастов. Так, L₂ = (n₁ + n₂)/2. Затем рассчитать T₂ = L₂ + L₃ + L₄ + L₅ + L₆ + L₇ + L₈, а потом уже определить величину е₂: е₂ = T₂/n₂. Обратите внимание на то, что величина ожидаемой продолжительности жизни меняется с возрастом, причем сначала она возрастает (из-за того, что очень много особей погибает в раннем возрасте, в течение первых двух лет), а затем падает.

Приведенная выше таблица выживания балянусов относится к типу так называемых «когортных» (или «динамических»), поскольку построена по данным наблюдений за динамикой смертности в одной конкретной когорте. Составить такие таблицы можно только в тех случаях, когда имеется реальная возможность проследить за индивидуальной судьбой всех членов достаточно большой выборки из определенной когорты. Сравнительно легко это было сделать для популяции балянусов, каждый из которых пожизненно прикреплен к скале, но и в этом случае потребовались регулярные обследования на протяжении 10 лет. Собрать аналогичный материал для организмов, ведущих подвижный образ жизни, или для организмов, характеризующихся большой продолжительностью жизни, гораздо труднее. Существует, однако, другой способ построения таблиц выживания. Вместо того чтобы наблюдать за отдельной когортой в течение периода, приближающегося по времени к максимальной продолжительности жизни, исследователь может в течение относительно короткого промежутка времени наблюдать за смертностью в отдельных возрастных группах (т. е. в сосуществующие когортах), а, зная численность этих групп, рассчитать специфическую для каждого возраста смертность. Таким способом нередко пользуются демографы, поскольку проследить на протяжении почти столетия за судьбой по крайней мере тысячи людей, относящихся к одной когорте, с момента их рождения до момента смерти достаточно сложно, а порой и невозможно.

Таблица выживания, построенная на основании краткосрочных наблюдений за смертностью во всех возрастных группах, называется статической. Табл. 3 является примером статической таблицы для женской части населения Канады в 1980 г. Статическая демографическая таблица представляет собой как бы временной срез через популяцию. В том случае, когда в популяции со временем не происходит каких-либо существенных изменений повозрастной смертности (и рождаемости), статическая и когортная таблицы практически совпадают.

Таблица 3

Статическая демографическая таблица женского населения Канады на 1980 г. (по Krebs, 1985)

Возрастная группа	Количество человек в каждой возрастной группе	Число умерших в каждой возрастной группе	Смертность в расчете на 1000 человек, 1000 qx.
0—1			9,52
1—4			0,50
5—9			0,25
10—14			0,24
15—19			0,49
20—24			0,54
25—29			0,56
30—34			0,71
35—39			1,11
40—44			1,66
45—49			2,67
50—54			4,18
55—59			6,51
60—64			10,09
65—69			16,07
70—74			25,86
75—79			42,66
80—84			72,50
85 и больше			151,70

 

Нередко экологи имеют дело с таблицами выживания, по способу построения являющимися промежуточными между когортными и статическими. Так, например, в ряде учебников приводится ставшим уже классическим пример таблиц (и кривых) выживания популяции снежного барана (Ovis dalli dalli) в районе национального парка Мак-Кинли (Аляска). Исходным материалом для этой таблицы послужили данные А. Мура, который по падевым кольцам нарастания рогов определил возраст 608 особей снежного барана, погибших в обследуемом районе. Время, в течение которого могут сохраняться эти остатки, превышает длительность одного поколения. Поэтому фактически собранный материал охватывал по крайней мере несколько когорт.

 

Кривые выживания

 

Если мы построим график зависимости доли доживших особей l_х от возраста х, то получим кривую, называемую кривой выживания (дожития), или просто «l_х -кривой». На рис. 18 показана кривая выживания самцов и самок снежного барана, полученная по упомянутым выше данным А. Мура. Как видно из приведенного графика (по оси ординат—логарифмическая шкала!), смертность снежного барана велика в первые два года жизни (погибает более половины особей!), затем в течение нескольких лет она очень низка (почти 100 %-ная выживаемость), но затем, на 9—10-й (для самок) или на 11—12-й (для самцов) год, она резко возрастает, и к 13 годам практически все особи погибают. Интересно, что высокая смертность снежного барана, как в начале, так и в конце жизни обусловлена одним и тем же фактором — прессом хищника (волка). Кривая выживания снежного барана отражает, таким образом, возрастную динамику уязвимости этого вида к воздействию хищника.

В настоящее время исследователями собран большой материал по кривым выживания для представителей разных групп организмов. Р. Перль, введший в 1920-х гг. в экологию понятие о кривых выживания, выделил три основных типа их (рис. 19), связанных между собой всевозможными промежуточными вариантами.

Кривая I типа (сильно выпуклая) соответствует ситуации, при которой смертность ничтожно мала в течение большей части жизни, но затем резко возрастает, и все особи погибают за короткий срок. Такое распределение смертности можно наблюду у дрозофил, поденок и других насекомых, которые выходят из куколок, через некоторое время спариваются, а после откладки яиц в массе гибнут. Вслед за Перлем такую кривую называют иногда «кривой дрозофилы», но не следует забывать, что моментом «рождения» (нулевым возрастом) в данном случае условно считается вылупление взрослых (имагинальных) стадий. Если проанализировать также гибель яиц, личинок и куколок, то кривая выживания будет иметь более сложный вид, и только ее правая часть будет соответствовать кривой I типа. К кривой I типа приближается кривая выживания человека в развитых странах, а в некоторой степени и кривые выживания крупных млекопитающих.

Кривая III типа (сильно вогнутая) иллюстрирует другой крайний случай — массовую гибель особей в начальный период жизни, а затем относительно низкую смертность оставшихся особей. Данный тип кривой выживания иногда называют типом устрицы (Ostrea), поскольку у этого моллюска, ведущего во взрослом состоянии прикрепленный образ жизни, есть планктонная личинка, и именно на стадии личинки наблюдается чрезвычайно высокая смертность особей. Для тех же устриц, которые избежали гибели на личиночной стадии и успешно осели на субстрат, шанс выжить резко повышается. По-видимому, распределение смертности, описываемое кривой III типа, довольно широко распространено в природе. Оно свойственно не только устрицам и другим донным беспозвоночным, имеющим планктонных личинок, но практически всем организмам, характеризующимся большой плодовитостью и отсутствием заботы о потомстве. Так, например, широко распространенного вида морских рыб — макрели (Scomber scombrus) — в течение первых 50—70 дней (до достижения ими длины 50 мм) гибнет 99,9996 % личинок. Если моментом начала жизни у макрели считать момент оплодотворения, то средняя продолжительность их жизни будет измеряться всего 12 ч, но у особей, достигших возраста 2—3 мес., имеется уже значительный шанс прожить еще несколько лет.

Кривая II типа (диагональная) соответствует постоянной, т.е. независимой от возраста, смертности в течение всей жизни. Другими словами, это значит, что в течение каждого возрастного интервала гибнет одна и та же доля от численности когорты в начале этого интервала[23]. Хотя может показаться, что смертность, независимая от возраста, маловероятна, на самом деле существует довольно много свидетельств именно такого распределения смертности по возрастам для разных групп организмов. Так, например, диагональные кривые выживания встре чаются среди рыб, пресмыкающихся, птиц, многолетних травянистых растений и т. д. (рис. 20). Правда, во всех этих случаях начало отсчета ведется от организмов, уже прошедших ранние, как правило, наиболее уязвимые стадии развития. Так, например, данные по птицам получены анализом гибели окольцованных птиц, но окольцовывают птиц обычно перед вылетом из гнезда, а гибель яиц и птенцов на ранних стадиях остается неучтенной.

Реально встречающиеся кривые выживания нередко представляют собой некоторую комбинацию указанных выше «основных» типов. Так, например, характерная для крупных млекопитающих кривая I типа почти всегда в самом начале круто падает вниз, что соответствует значительной смертности сразу после рождения. Даже в современных популяциях людей в развитых странах сохраняется повышенная смертность в первый год жизни (рис. 21).

Надо отметить, что кривая выживания человека далеко не всегда и не везде имела выпуклую форму, характерную для современных развитых стран. Так, например, проведенный по надписям на надгробных памятниках анализ дат жизни людей, живших в Римской империи в I—IV веках н. э., позволил построить кривые, оказавшиеся в некоторых случаях практически диагональными (рис. 22). Из приведенного рисунка следует, что в любом возрасте выживаемость, как мужчин, так и женщин были выше в провинции (Северная Африка), чем в самом городе Риме. Кроме того, на данном рисунке видно, что наклон кривой выживания женщин Рима резко увеличивается (кривая пересекается с кривой выживания мужчин) примерно в двадцатилетнем возрасте, что, очевидно, соответствует высокой смертности в начале периода деторождения.

Экспоненциальная модель роста численности популяции. Формулировка модели и ее основные условия

 

Чтобы разобраться в основных закономерностях, определяющих рост численности популяций, обратимся к простому примеру. Пусть некий одноклеточный организм, размножающийся простым делением (например, какая-нибудь инфузория), совершав одно деление раз в 4 ч. Тогда в результате деления этого организма через 4 ч будет уже 2 особи, через 8—4, через 12—8 через 16—16, через 20—32, через 24—64, через 28—128, через 32 4—256 и т. д. График показывающий данный рост (рис. 23,а),—это кривая, описываемая так называемым экспоненциальным законом Соответствующее уравнение имеет вид N_t = N₀e^rt, где N_t — численность популяции в момент времени t, N₀ — численность популяции в начальный момент t₀, е — основание натуральных логарифмов (2,7182), а r —показатель, характеризующий темп размножения особей в данной популяция (иногда этот показатель называют «специфической», или «врожденной, скоростью популяционного роста). Для того чтобы экспоненциальный рост численности продолжался в течение некоторого времени, необходимо только одно условие: постоянное значение показателя r.

Выше мы уже определяли мгновенную удельную скорость ро cта популяции как r = dN/Ndt. Это выражение можно записать и как dN/dt = rN. В такой форме записи подчеркивается, что скорость роста численности популяции пропорциональна самой численности. Если r = const, то рост происходит по экспоненциальному закону. В том случае, когда величины численности приводятся в логарифмическом масштабе, график экспоненциального роста приобретает вид прямой линии (рис. 23, б). Поэтому иногда экспоненциальный рост называют логарифмическим. Уравнение экспоненциального роста в логарифмической форме имеет следующий вид: lnN_t = lnN₀ + rt, т. е., по сути, это просто уравнение прямой, причем коэффициент r характеризует угол наклона ее к осям.

Во многих популярных руководствах по экологии говорится, что экспоненциальный рост популяций возможен только в особо оптимальных условиях, при отсутствии каких-либо ограничивающих факторов. Это не совсем верно, поскольку, как уже подчеркивалось выше, единственное (необходимое достаточное) условие такого роста — постоянство коэффициента г, отражающего, по сути дела, скорость размножения данных организмов. Так, например, проведя серию наблюдений за ростом популяций какого-либо одноклеточного организма в разных температурных условиях, нетрудно заметить, что с уменьшением температуры скорость деления клеток падает, но экспоненциальный характер роста сохраняется во всех вариантах (рис. 24, а).

Скорость экспоненциального роста популяций может использоваться как показатель благоприятности условий среды для данных организмов. Очевидно, например, что с повышением температуры у пойкилотермных животных эта скорость растет, но с приближением к границе толерантности снижается. У разных видов характер этих изменений может быть различным. На рис. 24, б приведены экспериментальные оценки зависимости скорости популяционного роста двух видов жуков Calandra oryzae и Rhizopertha dominica от температуры и влажности.

Математические формулы, описывающие закономерности экспоненциального роста, были приведены А. Лоткой в 1920-х гг. (см. Lotka, 1925), но основной принцип экспоненциального роста (или, как его чаще называли, роста в геометрической прогрессии) был известен уже очень давно. О том, что принципиально такой рост возможен, упоминали Ж. Бюффон и К. Линней. До них, еще в конце XVII в. особенности экспоненциального роста были очевидны одному из основателей демографии—Дж. Гранту[24]. О геометрической прогрессии как о некотором законе роста народонаселения писал и Томас Мальтус (1766—1834), труды которого оказали большое влияние на формирование взглядов двух исследователей, выдвинувших идею естественного отбора,—Ч. Дарвина и А. Уоллеса. Именно врожденная способность любой группы организмов неограниченно увеличивать свою численность по экспоненциальному закону служит одной из основных предпосылок теории естественного отбора. Известно, что сам Дарвин рассчитал потенциальные возможности роста популяций разных организмов. Так, согласно его оценкам, число потомков одной пары слонов — животных, размножающихся чрезвычайно медленно, — через 750 лет достигнет 19 млн. Если же обратиться к наиболее быстро размножающимся организмам и рассчитать возможные результаты их экспоненциального роста, то цифры получаются просто фантастические. Если, например, какая-нибудь бактерия в благоприятной питательной среде делится каждые 20 мин, то при сохранении таких темпов деления потомство одной бактериальной клетки через 36 ч дает массу, покрывающую весь земной шар сплошным слоем толщиной 30 см, а еще через 2 ч толщина этого слоя достигнет 2 м.

Поскольку ни бактерии, ни слоны не покрывают землю сплошным слоем, очевидно, что на самом деле в природе экспоненциальный рост популяций организмов или не происходит вообще, или же происходит, но в течение очень непродолжительного времени, сменяясь затем спадом численности или выходом ее на стационарный уровень. Предваряя возможный вопрос о том, зачем уделять столько внимания процессу, в природе практически не наблюдаемому, следует специально подчеркнуть, что модель экспоненциального роста используется в экологии в первую очередь для того, чтобы охарактеризовать (причем количественно!) потенциальные возможности популяции к росту. Оценивая разность между той численностью, которая могла бы быть достигнута популяцией при сохранении в течение некоторого времени экспоненциального роста, и той, которая реально наблюдалась через это время, можно практически измерить интенсивность смертности (или эмиграции), а проанализировав информацию о динамике смертности, выявить и факторы, ограничивающие рост изучаемой популяции. Характерно, что уже исследователи XVII—XVIII вв. использовали представление об экспоненциальном росте именно для описания потенциальных возможностей популяций.

⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: