Логистическая модель роста популяции

Для описания S-образного роста может быть использовано множество различных уравнений, но наибольшую популярность получило самое простое из них — так называемое логистическое. Впервые предложенное как модель роста народонаселения в 1838 г. бельгийским математиком П.-Ф. Ферхюльстом (Verhulst 1838)[27], оно было переоткрыто заново американскими исследователями Р. Перлем и Л. Ридом (Pearl, Reed, 1920) в 1920 г., которые, впрочем, уже через год признали приоритет Ферхюльста.

В основе логистической модели (рис. 29) лежит очень простое предположение, а именно линейное снижение скорости удельного роста r = dN/Ndt по мере возрастания численности N, причем скорость эта становится равной нулю при достижении некоторой предельной для данной среды численности К. Следовательно, если N = K, то r_а = 0. Логистическое уравнение нагляднее всего записать в дифференциальной форме:

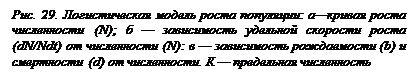
где r_maх — константа экспоненциального роста, который мог бы наблюдаться в начальный момент увеличения численности (теоретически при N = 0, или, как говорят иногда, в «конкурентном вакууме»). В популярных учебниках экологии иногда не совсем верно постоянный коэффициент из логистического уравнения r_maх приравнивают к показателю любого экспоненциального роста данной популяции, т. е. утверждается, что r_maх = r_a. На самом деле это не так: для соблюдения экспоненциального роста необходимо, чтобы показатель r_a был постоянной величиной (r_a = const), для осуществления же логистического роста необходимо, чтобы показатель r_a снижался по линейному закону при увеличении численности N. Напомним, что r_a как в уравнении экспоненциальном, так и в уравнении логистическом равно разности удельной рождаемости и удельной смертности. При логистическом росте r_a почти равно r_max только при численности, близкой к нулю, т. е. тогда, когда рождаемость b максимальна, а смертность d минимальна. Линейный характер изменения r_a при увеличении N подразумевает линейное изменение, как рождаемости, так и смертности (см. рис. 29). В интегральной форме логистическое уравнение имеет вид где N_t — численность популяции в момент времени t, е— основание натуральных логарифмов, а а — «постоянная интегрирования». Величину К можно трактовать как меру «емкости среды» в отношении особей данного вида (точнее, данной популяции).

Многие экологи 20—30-х гг., особенно имевшие дело с лабораторными культурами организмов, отнеслись с большим энтузиазмом к использованию логистического уравнения для описания экспериментальных данных. Энтузиазм этот объяснялся, видимо, тем, что S-образный (в широком смысле этого слова) рост популяций действительно наблюдался очень часто, а логистическое уравнение, сколь бы ни было оно несовершенным[28], описывало этот рост и, таким образом, служило первой моделью динамики численности, позволяющей говорить об общих закономерностях этого процесса.

Р. Перль и Л. Рид предполагали, что логистическая кривая хорошо описывает рост народонаселения в США до того момента, когда они проводили свое исследование (т. е. до 1920 г., а в более поздней публикации—и до 1940 г.), но, как сейчас ясно, действительно наблюдавшееся тогда соответствие динамики населения логистической модели не могло служить основанием для прогноза дальнейшего хода этого процесса[29]: численность населения США в последующие годы возрастала гораздо быстрее, чем этого следовало бы ожидать на основании логистической кривой.

Логистическая кривая не раз использовалась и при описании, результатов лабораторных опытов по культивированию тех или иных мелких организмов в ограниченном пространстве (сосуде, садке и т. п.) при ограниченном поступлении пищевых ресурсов. Такие зависимости в 20—40-е гг. были получены для бактерии, дрожжей, простейших, мелких ракообразных и ряда насекомых. Изучая рост популяций дрожжей Saccharomyces cerevisiae и Schizosaccharomyces kephir, Г. Ф. Гаузе показал, что значение предельной плотности (оцениваемой величиной /С) для этих видов неодинаково: для Saccharomyces она в 2 раза выше, чем для Schizosaccharomyces, причем различие это, как выяснилось, связано с тем, что второй вид вырабатывает примерно в 2 раза больше этилового спирта, чем первый, а именно накопление спирта в. среде и тормозит дальнейший рост дрожжей. Если продукты метаболизма удаляются из среды или не оказывают тормозящего действия на размножение организмов, то величина предельной плотности определяется соотношением интенсивности поступления в среду пищи и интенсивности потребления ее организмами (т. е. их рационом). На лабораторных культурах ветвистоусого рачка Daphnia obtusa Л. Слободкин (Slobodkin, 1954) показал, что, добавляя в разные варианты разное количество корма (взвеси одноклеточной водоросли Chlamydomonas), можно непосредственно влиять на предельную плотность К., причем величина этой плотности линейно возрастает при увеличении количества задаваемой пищи.

Логистическая модель, как уже подчеркивалось выше, основывается на очень простых постулатах, которые не выводимы из свойств организмов, однако мы можем себе представить, какими чертами необходимо обладать организмам, чтобы рост их популяции с большей вероятностью описывался логистической кривой. Во-первых, все особи популяции должны быть одинаковыми, т. е. потреблять одно и то же количество пищи (и других ресурсов), при возрастании плотности популяции для них в равной степени должна возрастать вероятность гибели и (или) снижаться вероятность оставить потомство. Во-вторых, реакция этих организмов на возрастание плотности популяции, проявляющаяся в снижении рождаемости и увеличении смертности, должна быть практически мгновенной. Хотя ни один реальный вид организмов такими свойствами не обладает, очевидно, что простейшие или бактерии, т. е. существа мелкие и размножающиеся простым делением, ближе к такому идеалу, чем крупные многоклеточные организмы, характеризующиеся сложным циклом развития и сложной размерно-возрастной структурой популяции. Очевидно также, что, четко осознавая, чем и в какой степени реальные организмы отличаются от идеального объекта логистической модели, исследователь может сделать эту модель более реалистичной, вводя в нее те или иные усложнения, учитывая, например, размерную структуру популяции и эффект запаздывания.

Предположение о линейной зависимости скорости роста популяции от ее плотности (основное условие логистического роста) Ф. Смит (Smith, 1963) проверил экспериментально на лабораторной популяции рачка Daphnia magna. Увеличивая объем сосуда с питательной средой, в котором содержались дафнии, Ф. Смит в течение некоторого времени поддерживал плотность растущей популяции на одном уровне. Определив таким образом при разных плотностях значения удельной скорости популяционного роста, Ф. Смит построил по экспериментальным данным график, отражающий взаимосвязь данных величин. В соответствии с логистической моделью ожидалось, что график этот будет прямой линией, однако на самом деле получилась вогнутая кривая, т. е. при низкой плотности популяция росла быстрее, чем это было бы при линейной зависимости, а при высокой — медленнее. Учтя эти данные и соответствующим образом модифицировав модель, Смит добился гораздо лучшего соответствия ее результатам эксперимента.

Чтобы логистическая модель была более реалистичной, в частности, чтобы она лучше описывала динамику популяции не только на начальном этапе ее развития, необходимо учитывать и наблюдающееся практически в каждой популяции запаздывание реакции организмов (проявляющейся как их гибель или размножение) на изменения, произошедшие в окружающей среде. Так, например, у часто используемых в лабораторных экспериментах дафний самки отвечают на улучшение пищевых условий откладкой в выводковые камеры очередных порций партеногенетических яиц. Эта реакция довольно быстрая, но не мгновенная: если ранее дафния голодала, то в ее теле сначала должны образоваться пузырьки с жироподобным веществом, которые затем сосредоточатся около яичников, и запас энергоемких веществ перейдет непосредственно в созревающие ооциты — на все это уйдет минимум 2—3 дня. После того как яйца отложены в выводковую камеру, пройдет еще время, в течение которого в них сформируются эмбрионы, и только спустя 2—5 сут. (срок зависит от температуры) из них вылупляются молодые рачки, способные самодеятельно плавать и отфильтровывать пищу. Но за те несколько дней, которые минули с момента улучшения пищевых условий в окружающей среде до момента появления на свет молодых рачков, концентрация пищи в водоеме (или в экспериментальном сосуде) могла существенным образом измениться. Если она даже не изменилась к моменту выхода из яиц рачков, она с большой степенью вероятности может измениться (сократиться) после того, как масса недавно отрожденных особей приступит к самостоятельному питанию. К этому времени, однако, самки успеют отложить новые яйца, а вылупившиеся из них молодые рачки окажутся уже в явно неблагоприятных пищевых условиях. Ответом на наступившее голодание будет резкое сокращение интенсивности откладки яиц, а также гибель особей, причем в первую очередь молодых, характеризующихся более интенсивным удельным (на единицу массы тела) метаболизмом, но не имеющих значительных энергетических запасов (взрослые самки такими запасами обладают и при не очень сильном голодании могут спастись от гибели ценой прекращения размножения).

Очевидно, в популяциях дафний, существующих в условиях регулярного поступления постоянного количества корма, с большой степенью вероятности следует ожидать возникновения колебаний численности, которые по сути своей являются автоколебаниями, т. е. колебаниями, вызванными не изменениями факторов, внешних по отношению к системе «пища—потребитель», а колебаниями, связанными с несовершенством самого способа регуляции численности, точнее, установления соответствия численности (и биомассы!) популяции тому количеству пищи, которое имеется в данный момент в среде. Подобные автоколебания нередко действительно возникают в популяциях дафний, а также многих других животных, культивируемых в лабораторных условиях при регулярном снабжении постоянным количеством пищи.

Пожалуй, наиболее известный пример колебаний такого рода приведен австралийским энтомологом А. Никольсоном (Nicholson, 1954), экспериментировавшим с лабораторными популяциями падальной мухи Lucilia cuprina. Взрослые особи этого вида могут долго существовать в садке, питаясь только сахаром и водой, но, чтобы отложить яйца, им обязательно нужно потребить определенное количество белковой пищи. Личинки L. cuprina живут в природе в трупах животных, а в лаборатории их удается успешно доводить до окукливания на кусочках печени. В долгосрочных (продолжающихся иногда более года) опытах, при условии ограниченного количества белковой пищи для взрослых и неограниченного — для личинок, вся популяция совершала правильные циклические колебания (рис. 30) с максимумами через каждые 30—40 дней. Механизм возникновения этих колебаний ясен: при достижении слишком высокой плотности вылетающим из куколок взрослым мухам не хватало белковой пищи, и поэтому только отдельным самкам удавалось отложить яйца. Соответственно резко снижалась численность следующего поколения. В условиях пониженной численности взрослых особей белковой пищи хватало практически на всех самок, и в последующий период происходило быстрое нарастание численности популяции, после чего снова начинало сказываться пищевое лимитирование, — и весь цикл повторялся. В других сериях опыта А. Никольсон снабжал взрослых мух избытком полноценной пищи, но строго ограничивал количество пищи для личинок. При этом также возникали колебания численности, вызванные тем, что при высокой плотности личинок подавляющему большинству из них не хватало пищи для завершения метаморфоза и превращения в куколку. Таким образом, основная причина возникновения колебаний при лимитировании пищей личинок — это периодическое повышение смертности, а при лимитировании пищей взрослых—периодическое снижение рождаемости.

Запаздывание (или, как иногда говорят, лаг-эффект) в реакции скорости роста популяции на ее плотность (подчеркнем, что речь идет о формальном выражении—на самом деле это может быть реакция не на саму плотность, а на количество пищи, приходящееся на одну особь) может быть учтено в логистической модели, которая примет следующий вид: , где dN/dt — скорость изменения численности в момент t, N_t — численность в момент t, a N_t-τ — численность, наблюдавшаяся за время t до момента τ. В случае популяций дафнии t можно трактовать как промежуток времени между моментом образования яиц (в ответ на улучшение пищевых условий) и моментом выхода из этих яиц молоди. Теоретическое исследование логистической модели с запаздыванием показало, что ей свойствен колебательный режим, причем при увеличении времени запаздывания и величины максимальной скорости (r_mах) возрастают амплитуда и частота таких колебаний.

Существуют и более сложные модификации логистического уравнения, например описывающие динамику популяций с дискретными, неперекрывающимися поколениями, или учитывающие влияние случайно (стохастически) меняющихся внешних условий на скорость роста популяции или на величину равновесной плотности (К). Порожденная такими моделями динамика численности может быть достаточно сложной и порой практически неотличимой от динамики, определяемой чисто стохастическими процессами.