Разрешимые и неразрешимые проблемы

 

Общепринятой является точка зрения, согласно которой алгоритм считается эффективным, если он имеет полиномиальную сложность. Дело в том, что несмотря на усилия многих специалистов, для решения таких задач, как задачи отыскания в графе наибольшего независимого множества, гамильтонова цикла, k -раскраски и ряда других, до сих пор не найдено полиномиальных алгоритмов. Более того, имеются веские доводы, позволяющие предположить, что таких алгоритмов не существует. Обсуждению этих доводов и посвящен данный раздел.

Начнем с внесения изменений в вычислительную модель. Будем считать, что каждая ячейка абстрактной вычислительной машины может содержать только 0 или 1, и целые числа рассматриваются в двоичной системе счисления. В соответствии с этим всякое целое число a ≠ 0, 1 займет ]log |a|[ ячеек машинной памяти (] x [ – наименьшее целое, не меньшее чем x). Рациональное число, не являющееся целым, будем рассматривать в виде несократимой дроби и представлять в машине как упорядоченную пару целых чисел – числитель и знаменатель этой дроби. Время выполнения каждой элементарной операции примем равным сумме длин записей ее операндов в двоичной системе счисления.

Далее будем рассматривать каждую задачу в так называемом распознавательном варианте, когда решение задачи заключается в получении ответа «да» или «нет». Всякий алгоритм решения такой задачи, будучи примененным к соответствующему входу, работает какое-то время и затем, сообщив ответ «да» или «нет», останавливается. Для некоторых задач их «естественные» постановки уже являются распознавательными. Таковы, например, задачи распознавания изоморфизма, гамильтоновости, планарности, эйлеровости графов. Однако чаще (а на практике – как правило) исходная постановка задачи является оптимизационной. В оптимизационной задаче требуется выбрать из множества допустимых решений X такое решение x, вес (или стоимость) которого w(x) минимален. В рассмотренных вами оптимизационных задачах в качестве X фигурировали множества остовов, путей с заданной начальной вершиной или паросочетаний данного графа. Каждой оптимизационной задаче сопоставим ее распознавательный вариант, который выглядит следующим образом. По данным множеству X, весовой функции w и числу k требуется определить, существует ли элемент x ÎX такой, что w(x) £ k. Очевидно, что имея полиномиальный алгоритм решения оптимизационной задачи, легко получить полиномиальный алгоритм решения соответствующей ей распознавательной задачи. Можно показать. Что при довольно необременительных предположениях относительно функции w верно и обратное. Мы не будем на этом останавливаться, поскольку для дальнейшего нам достаточно только знать, что оптимизационная задача «не проще» соответствующей распознавательной.

Итак, далее рассматриваются только распознавательные задачи. Определим P как класс распознавательных задач, каждая из которых может быть решена некоторым алгоритмом за полиномиальное время. Мы уже знаем, что в этот класс входят задачи о минимальных остовах, кратчайших путях и наибольших паросочетаниях (имеются в виду распознавательные постановки этих задач, как было установлено). В то же время было названо несколько задач, принадлежность которых к классу P не установлена и считается сомнительной.

Теперь сделаем следующее важное наблюдение. Все задачи, с которыми мы сталкивались до сих пор, независимо от того, установлена их принадлежность классу P или нет, обладают одним общим свойством: если вход задачи таков, что имеет место ответ «да», то существует полиномиальный алгоритм, доказывающий этот факт. Поясним сказанное на примере. Пусть задача состоит в выяснении, является ли граф гамильтоновым, и пусть поступающий на вход граф G гамильтонов, т. е. в графе G имеется гамильтонов цикл C. Тогда доказательство гамильтоновости графа G заключалось бы в проверке включения C Í G. Если, например, граф G задан матрицей смежности, то эту проверку можно выполнить с помощью очевидного алгоритма, затратив O (n) операций. Подчеркнем, что речь идет лишь о существовании полиномиального доказательства – чтобы иметь это доказательство в своем распоряжении, надо знать цикл C. Положение иное, если граф G не является гамильтоновым. В этом случае нельзя утверждать даже, что полиномиальное доказательство этого факта существует. Можно, конечно, перебрать все (| G |-1)! простых циклов длины | G | полного графа, проверяя каждый раз, содержится ли цикл в графе G. Однако подобное доказательство требует времени по крайней мере O ((| G |-1)!), и, следовательно, не является полиномиальным.

Теперь мы хотим определить еще один класс распознавательных задач, включив в него все задачи, обладающие тем свойством, что если вход задачи имеет ответ «да», то существует полиномиальный алгоритм, проверяющий (доказывающий) этот факт. С этой целью дополним множество обычных операторов, из которых мы составляли алгоритмы, одним особым. Пусть A = A ₁, A ₂ ,…, A _m – последовательность, элементами которой служат обычные операторы и один особый, запись которого имеет вид B(l ₁, l ₂), l ₁, l ₂Î{1, 2, …, m}. Пусть, далее, Q= q ₁, q ₂, …, q _p – такой список, что q _i =l ₁ либо q_i=l₂ (i= 1, p). После того, как A и Q заданы, действие особого оператора B(l₁, l₂) определим так: в результате k -го (k£p) выполнения этого оператора управление передается оператору А_l 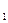, если q_k=l₁, и A_l 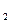, если q_k=l₂, а при k>p вычисления прекращаются. Итак, последовательности операторов A и списку Q ставится в соответствии обычный (детерминированный) алгоритм. Этот алгоритм будем обозначать через A _Q, чтобы подчеркнуть наличие двух компонент A и Q. Список Q будем при этом называть угадывающей последовательностью, а последовательность A – недетерминированным алгоритмом. Подчеркнем особо, что недетерминированный алгоритм не является алгоритмом, а представляет собой чисто абстрактную конструкцию.

Будем говорить, что недетерминированный алгоритм А решает распознавательную задачу за полиномиальное время, если найдется такой полином р(п), что выпол­няется следующее условие: каждый вход длины п этой задачи имеет ответ «да» тогда и только тогда, когда для него существует такая угадывающая последовательность Q, что алгоритм A_Q, будучи примененным к этому вхо­ду, останавливается, сообщив ответ «да», и время его работы не превосходит р{п). Заметим, что согласно это­му определению каждому входу с ответом «да» должен ставиться в соответствие свой алгоритм A_Q. От этого ал­горитма не требуется ничего иного, кроме правильной реакции на свой вход. Поведение алгоритма на всех дру­гих входах для нас безразлично.

Задача недетерминированно разрешима за полиноми­альное время, если существует недетерминированный ал­горитм, решающий ее за это время.

Определим теперь NР как класс всех распознаватель­ных задач, недетерминированно разрешимых за полино­миальное время.

Нетрудно видеть, что Р ^Í NР. Действительно, полино­миальный алгоритм решения всякой задачи из Р можно превратить в полиномиальный алгоритм вида A_Q, доба­вив оператор В (l ₁, l ₂ ) так, чтобы он ни разу не сраба­тывал. При этом в качестве Q можно взять произволь­ную последовательность, например, состоящую из одного элемента. Класс NР чрезвычайно широк. Например, боль­шинству задач, встречающихся в предыдущих главах, можно «естественным» образом сопоставить распознава­тельные задачи. При этом окажется, что почти все они принадлежат NР.

В качестве примера доказательства принадлежно­сти задачи к NР рассмотрим задачу об изоморфном подграфе, которую здесь сформулируем в следую­щем виде.

Даны два графа G ₁ и G ₂, причем VG ₁ = VG ₂ = V. Установить, существует ли такая подстановка s: V → V, для которой истинна импликация

(uv Î EG ₁) Þ (s(u)s(v)Î EG ₂).

Удобно рассматривать эту задачу в матричной постанов­ке. Пусть V={1, 2,..., п }, А ₁ и А ₂, – матрицы смеж­ности графов G ₁ и G ₂ соответственно. Обозначим через S матрацу подстановки s. Теперь задачу об изо­морфном подграфе можно сформулировать так: опреде­лить, существует ли такая матрица подстановки S, что все единицы матрицы SA ₁ S ^-1 содержатся среди единиц матрицы А ₂, т. е. что матрица (А ₂ —SА ₁ S ^-1 ) неотри­цательна.

Недетерминированный алгоритм A для решения этой задачи выглядит следующим образом.

1. Выполнить пп. 2 – 4 для всех k = и перейти к п. 5.

2. B (3,4).

3. t_k =0.

4.t_k=1.

5. S_ij:= t_i(n-1)+j для всех i, j = .

6. А':= SA ₁ S ^-1.

7. Если матрица А ₂– А' неотрицательна, то конец и ответ «да». Иначе – конец.

Напомним, что S_ij – элемент матрицы S, занимающий позицию (i, j).

Покажем теперь, как выбирать угадывающую после­довательность Q. Рассмотрим произвольный вход задачи, имеющий ответ «да». Это – пара симметрических (0,1)-матриц А ₁ и А ₂, для которой существует такая матрица подстановки S, что А ₂ – SA ₁ S ^-1 –неотрицательная мат­рица. Заменим в матрице S 0 на 3 и 1 на 4 и в качестве Q возьмем последовательность элементов этой новой мат­рицы, выписанных по строкам.

Работа алгоритма A_Q состоит из двух этапов. На пер­вом этапе (пп. 1 – 5) с помощью Q строится матрица подстановки, обеспечивающая изоморфное вложение. Со­держанием второго этапа (пп. 6, 7) является проверка того, что матрица S обладает нужным свойством. Полиномиальность алгоритма A_Q очевидна.

Напомним, что частными случаями задачи об изо­морфном подграфе являются задачи об изоморфизме гра­фов, о существовании в графе гамильтонова цикла или клики заданного размера и ряд других. Таким образом, попутно установлена принадлежность всех этих задач к классу NР. Доказательство этого свойства для других графовых задач проводится, как правило, столь же про­сто. При этом работа алгоритма A_Q, так же как и в предыдущем случае, распадается на два этапа: 1) по­строение некоторого варианта, 2) проверка того, что этот вариант подходящий. Например, в задаче о k -раскраске вершин графа такой алгоритм сначала припишет верши­нам графа нужные цвета, а затем проверит, что любые две вершины одного цвета не смежны.

Тот факт, что большинство «естественных» задач вхо­дит в класс NР, свидетельствует о чрезвычайной важ­ности вопроса: совпадают ли классы Р и NP? Эта не ре­шенная до сих пор проблема считается важнейшей в науке о вычислениях. Большинство исследователей скло­няется к мнению, что Р≠NР. На первый взгляд ситуа­ция Р≠NР не лишает нас возможности получить в бу­дущем полиномиальный алгоритм решения какой-либо из задач, названных нами «трудными». Однако это не так. Как оказалось, из Р≠NР следует, что ни одна из этих «трудных» задач не имеет полиномиального алго­ритма, а из существования такого алгоритма для одной из них следует, что Р = NР.

Изложение соответствующих результатов опирается на понятие сводимости одной задачи к другой. Предло­жение «задача А сводится к задаче B» означает, в обще­принятом смысле, что из решения задачи В можно по­лучить решение задачи А. Нам необходимо уточнить это понятие так, чтобы оно учитывало вычислительные за­траты, связанные с получением решения одной задачи из решения другой.

Пусть существует полиномиальный алгоритм F, кото­рый, будучи примененным ко всякому входу I задачи А, строит некоторый вход F(I) задачи В. Если при этом вход I имеет ответ «да» тогда и только тогда, когда от­вет «да» имеет вход F(I), то говорят, что задача А по­линомиально сводится к задаче В, и пишут А µ В. По­скольку сводимостей, отличных от полиномиальной, мы не рассматриваем, то слово «полиномиально» в дальней­шем будем опускать и говорить просто «А сводится к B».

Нетрудно показать, что если задача А сводится к за­даче В и В Î P, то и А Î Р. Действительно, пусть A – алгоритм решения задачи В и полиномы р ₁ (п), р ₂ (п) таковы, что 0(р ₁ {п)) и 0(р ₂ (п)) –сложности алгорит­мов F и Aсоответственно. Рассмотрим теперь алгоритм A’ решения задачи А, состоящей из двух этапов. На первом этапе вход I задачи А преобразуется алгорит­мом F во вход F (I) задачи В. На втором этапе алгоритм Aприменяется ко входу F(I). Согласно определению F, алгоритм Aсообщит ответ «да» тогда и только тогда, когда вход I имеет ответ «да», т. е. алгоритм A ' дей­ствительно решает задачу А. Выясним теперь его слож­ность. Если длина I равна n, то F(I) будет построен за время 0(р ₁ (п)), и его длина – О (p₁ (n)). При этом алгоритм A, будучи примененным ко входу F(I), затра­тит время 0(p ₂ (p₁(n))). Таким образом, сложность алго­ритма A ' есть 0(p ₁ (n)+р₂(р ₁ (п)}). Поскольку супер­позиция и сумма полиномов также являются полинома­ми, то A ' — полиномиальный алгоритм.

Точно так же можно показать, что из А µ В и B µ С следует А µ С.

Задачу А назовем NP-полной, если A Î NP и любая задача из NP сводится к А.

Из этого определения и предыдущих рассмотрении сразу следует, что Р = NP, если хотя бы одна NP -полная задача входит в Р.

Говоря неформально, каждая NP -полная задача «не проще», чем любая задача из NP. Поэтому, доказав NP -полноту некоторой задачи, мы получаем веские осно­вания считать ее трудной. Для доказательства NP- полноты задачи достаточно установить ее принадлежность к NP и показать, что к ней сводится некоторая NP -полная задача. Чтобы воспользоваться этой схемой, надо иметь в распоряжении хотя бы одну NP -полную задачу.

Первой задачей, относительно которой было показано, что она является NP -полной, была задача о выполни­мости. Пусть х ₁, x ₂, х ₃ ,...— булевы переменные, прини­мающие значения «истина» или «ложь», и 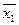, , ,… –их отрицания. Те и другие в совокупности называются литералами. Пусть символы V и Λ обозначают булевы операции дизъюнкции и конъюнкции соответственно. Формула и ₁ V u ₂ V... V u_m называется элементарной дизъ­юнкцией, если и ₁, u ₂,..., u_m – литералы. Пусть С ₁, С ₂,......, С_p – элементарные дизъюнкции. Тогда выражение вида С ₁ Λ С ₂Λ ... Λ С_p называется булевым выраже­нием в конъюнктивной нормальной форме. Булево выра­жение называется выполнимым, если входящим в него переменным можно так присвоить значения «истина» или «ложь», что значением выражения будет «истина». Не все выражения являются выполнимыми. Например, булево выражение

(x ₁V x ₂) Λ (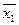 V x ₃) Λ ( V )

выполнимо, а выражение (x ₁V x₂)Λ (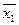 V )Λ(x ₁ V )Λ (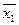 \/ x ₂) не выполнимо. Задача, о выполнимости (ВЫПОЛНИМОСТЬ) состоит в определении, является ли данное булево выражение в конъюнктивной нормаль­ной форме выполнимым.

Следующая теорема, приводимая здесь без доказа­тельства, лежит в основе теории NP -полноты.

Теорема 5.1(С. Кук, 1971 г.). Задача ВЫПОЛНИМОСТЬ является NP-полной.

В настоящее время известен значительный (и интен­сивно пополняющийся) список NP -полных задач. В этом списке находятся почти все задачи, получившие ранее репутацию трудных для алгоритмического решения. Ниже приведены только те из них, с которыми мы сталки­вались в предыдущих главах.

Некоторые NP -полные задачи.

КЛИКА: Даны граф G и натуральное число k. Опре­делить, содержит ли граф G клику мощности k.

НЕЗАВИСИМОСТЬ: Даны граф G и натуральное число k. Определить, содержит ли граф G независимое k -элементное множество вершин.

ИЗОМОРФНЫЙ ПОДГРАФ: Даны два графа G ₁ = (V, E ₁ ) и G ₂=(V, E ₂ ). Определить, существует ли под­становка s: V → V, для которой истинна импликация (uvÎ E ₁ ) Þ (s(u}s(v)ÎE ₂ ).

ВЕРШИННОЕ ПОКРЫТИЕ: Даны граф G и нату­ральное число k. Определить, существует ли в графе G вершинное покрытие мощности не более k.

ДОМИНИРУЮЩЕЕ МНОЖЕСТВО: Даны граф G и натуральное число k. Определить, существует ли в гра­фе G доминирующее множество мощности не менее k.

ГАМИЛЬТОНОВ ЦИКЛ: Дан граф G. Определить, содержит ли граф G гамильтонов цикл.

ЯДРО: Дан ориентированный граф G. Определить, содержит ли граф G ядро.

ВЕРШИННАЯ (РЕБЕРНАЯ) РАСКРАСКА: Даны граф G и натуральное число k. Определить, существует ли правильная k -раскраска вершин (ребер) графа G.

Рассмотрим в качестве примера доказательство NP -полноты задачи КЛИКА. Пусть L_k – граф, у которого некоторые k вершин образуют клику, а остальные п – k –изолированные вершины. Ранее мы установили, что задача ИЗОМОРФНЫЙ ПОДГРАФ принадлежит NP. Если в этой задаче положить G ₂ =G, где G – граф, фигурирующий в формулировке задачи КЛИКА, а в ка­честве G ₁ выбрать граф L_k, то получим задачу КЛИКА. Следовательно, задача КЛИКА принадлежит NP.

Покажем теперь, что ВЫПОЛНИМОСТЬ µ КЛИКА. Пусть B = C₁ V C₂ V... V C_m – произвольное булево вы­ражение в конъюнктивной нормальной форме, { u ₁, u ₂,..., u_p } – множество входящих в него литералов. Будем обозначать через C’_i множество литералов, входящих в элементарную дизъюнкцию C_i.

Поставим в соответствие выражению В граф G по следующему правилу:

VG={v_ij: u_i Î С'_i},

EG = {v_ij v_kl: u_i ¹ _i, j ¹ i }.

Таким образом, вершины графа G находятся во взаимно однозначном соответствии с вхождениями литералов в элементарные дизъюнкции. Две вершины смежны, если соответствующие вхождения не противоречат друг другу, т. е. элементарные дизъюнкции различны и оба литера­ла могут одновременно принять значение «истина».

Пусть в графе G имеется клика размера k = т. Этой клике соответствует набор таких т вхождений u_i 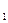Î C’ ₁, и _i 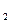Î С’ ₂,..., u_i Î C’_m, что u_i ¹ _i . Поэтому после при­своения всем u_i 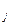(j= ) значения «истина» выраже­ние В также примет это значение, т. е. В – выполнимое выражение.

Наоборот, предположим, что В – выполнимое выра­жение. Пусть переменным присвоены значения «истина» или «ложь» так, что выражение В получило значение «истина». Тогда каждая элементарная дизъюнкция C_l должна содержать литерал u_i , имеющий значение «исти­на». Ясно, что при этом u_i ¹ _i . Следовательно, т вер­шин v _{1 i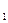} , v _{2 i} , …, v_mi попарно смежны в графе G, т.е. образуют клику размера т. Таким образом, выражение В выполнимо тогда и только тогда, когда в графе G име­ется клика размера k=т. Легко видеть, что построение графа G по выражению В можно выполнить за время O (р(п)), где р(п) – полином, а п – длина записи выра­жения В (длина входа задачи ВЫПОЛНИМОСТЬ).

Имеется ряд задач, входящих в NP, для решения ко­торых досих пор не найдено полиномиальных алгоритмов и относительно которых неизвестно, являются ли они NP -полными. Наиболее заметной графовой задачей среди них является задача об изоморфизме графов.

С другой стороны, большинство встречающихся на практике задач не являются распознавательными и, сле­довательно, не принадлежат классу NP. В то же время ко многим из них удается свести некоторые NP -полные задачи. В этой ситуации полезным оказывается следую­щее определение. Задача называется NP-трудной, если к ней сводится некоторая NP -полная задача. Новый тер­мин позволяет, например, избежать громоздких конструк­ций типа «распознавательный аналог задачи А является NP -полной задачей» и дает возможность говорить про­сто, что «задача А NP -трудна».

Теория NP -полноты, помимо теоретического, представ­ляет и чисто практический интерес. Доказав, что задача NP -трудна, разработчик алгоритмов получает достаточ­ные основания, чтобы отказаться от поиска эффектив­ного и точного алгоритма. Дальнейшие его усилия могут быть направлены, например, на получение приближен­ного решения, либо на получение решения в типичном случае (в большинстве случаев).

 

ЗАКЛЮЧЕНИЕ

 

Представленное учебное пособие не претендует на полноту рассмотрения всех направлений развивающейся в настоящее время дискретной математики. Автор лишь хотел ознакомить читателя в рамках выделенного на изучение курса времени с основными понятиями и подходами дисциплины. Предложенный материал может служить фундаментом для дальнейшего изучения как теоретических и прикладных вопросов дискретной математики, как в целом, так и отдельных ее направлений при изучении специальных дисциплин.

 

 

 

 

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

1. Емеличев В.А. Лекции по теории графов / В.А. Емеличев, О.И. Мельников. М.: Наука, 1990. – 384 с.

2. Кристофидес Н. Теория графов: алгоритмический подход / Н. Кристофидес. М.: Мир, 1978. – 432 с.

3. Свами М. Графы, сети и алгоритмы / М. Свами, К. Тхуласираман. М.: Мир, 1974. – 520 с.

4. Судоплатов С.В. Элементы дискретной математики: учебник / С.В. Судоплатов, Е.В. Овчинникова. М.: ИНФРА-М, 2002. – 280 с.

5. Леденева Т.М.Специальные главы математики. Дискретная математика: учеб. пособие / Т.М. Леденева. Воронеж: ВГТУ, 1997. – 130 с.

6. Новиков Ф.А. Дискретная математика для программистов / Ф.А. Новиков. СПб.: Питер, 2004. – 364 с.

7. Тишин В.В. Дискретная математика в примерах и задачах / В.В. Тишин. СПб.: БХВ-Петербург. 2008. – 352 с.

8. Гаврилов Г.П. Задачи и упражнения по дискретной математике: учеб. пособие / Г.П. Гаврилов, А.А. Сапоженко. – 3-е изд., перераб. М.: ФИЗМАТЛИТ, 2005. – 416 с.

9. Лавров И.А. Задачи по теории множеств, математической логике и теории алгоритмов / И.А. Лавров, Л.Л. Максимова. М.: ФИЗМАТЛИТ, 2004. – 256 с.

10. Кузнецов О.П. Дискретная математика для инженера / О.П. Кузнецов. СП.: Лань, 2005. - 400 с.

 

ОГЛАВЛЕНИЕ

 

ВВЕДЕНИЕ
1.	ЭЛЕМЕНТЫ ТЕОРИИ МНОЖЕСТВ
	1.1.	Основные понятия и определения теории множеств
	1.2.	Операции над множествами и их свойства. Диаграммы Эйлера-Венна
	1.3.	Мощность множества
	1.4.	Взаимно однозначное соответствие между множествами
	1.5.	Счетные и несчетные множества
		Задачи и упражнения
2.	ЭЛЕМЕНТЫ ТЕОРИИ ОТНОШЕНИЙ
	2.1.	Бинарные отношения. Свойства отношений
	2.2.	Отношение эквивалентности и разбиения
	2.3.	Отношение порядка. Диаграмма Хассе
		Задачи и упражнения
3.	ФУНКЦИИ, ОТОБРАЖЕНИЯ И ОПЕРАЦИИ
4.	ЭЛЕМЕНТЫ ТЕОРИИ ГРАФОВ
	4.1.	Основные понятия и определения теории графов
	4.2.	Типы графов
	4.3.	Матричные представления графов
	4.4.	Представление графов в ЭВМ
	4.5.	Операции над графами
	4.6.	Метрические характеристики графа. Расстояние в графах
	4.7.	Графы с заданной последовательностью степеней
	4.8.	Достижимость и связность
		4.8.1.	Основные определения
		4.8.2.	Матрицы достижимостей и контрдостижимостей
		4.8.3.	Нахождение сильных компонент
		4.8.4.	Базы и антибазы
	4.9.	Независимые и доминирующие множества
		4.9.1.	Нахождение всех максимальных независимых множеств
	4.10.	Покрытия и раскраски
	4.11.	Деревья, остовы и кодеревья
		4.11.1.	Основные определения
		4.11.2.	Алгортм построения остова неорграфа
		4.11.3.	Кратчайшие остовы
		4.11.4.	Обходы графа по глубине и ширине
		4.11.5.	Упорядоченные и бинарные деревья
	4.12.	Эйлеровы циклы. Гамильтонов контур
		4.12.1.	Метод Флери построения эйлерова цикла
		4.12.2.	Метод перебора Робертса и Флореса для построения гамильтоновых путей и контуров
		4.12.3.	Алгебраический метод выделения гамильтоновых путей и контуров
	4.13.	Плоские и планарные графы
		4.13.1.	Формула Эйлера
		4.13.2.	Критерии анализа планарности
		4.13.3.	Алгоритм укладки графа на плоскости
			Задачи и упражнения
5.	АЛГЕБРА ЛОГИКИ
	5.1.	Операции над высказываниями
	5.2.	Правила записи сложных формул
	5.3.	Таблицы истинности
	5.4.	Равносильность формул
	5.5.	Дизъюнктивные и конъюнктивные нормальные формы
		5.5.1.	Аналитический способ приведения к СДНФ
		5.5.2.	Табличный способ приведения к СДНФ
		5.5.3.	Табличный способ приведения к СКНФ
	5.6.	Минимизация булевых функций в классе ДНФ
	5.7.	Геометрическое представление булевых функций
		5.7.1.	Геометрический метод минимизации булевых функций
			Задачи и упражнения
6.	РАЗРЕШИМЫЕ И НЕРАЗРЕШИМЫЕ ПРОБЛЕМЫ
ЗАКЛЮЧЕНИЕ
БИБЛИОГРАФИЧЕСКИЙ СПИСОК

 

 

 

 

Учебное издание

 

Собенина Ольга Валерьевна

 

 

ДИСКРЕТНАЯ МАТЕМАТИКА

 

 

В авторской редакции

 

Компьютерный набор О.В. Собениной

 

Подписано к изданию 20.11.2012.

Уч-изд. л. 11,0.

 

ФГБОУ ВПО «Воронежский государственный технический университет»

394026 Воронеж, Московский просп., 14

⇐ Предыдущая12131415161718192021

Поделиться:

Воспользуйтесь поиском по сайту: