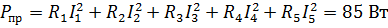|
2.7. Практикум. Преобразования электрических схем.
|
|
|
|
2. 7. Практикум. Преобразования электрических схем.
| Задача 1. 1 |  Схема 1. 1 Схема 1. 1
|
Определить  Ответ:
Ответ: 
| |
| Задача 1. 2 | Схема 1. 2 |
Определить  Ответ:
Ответ: 
| 
|
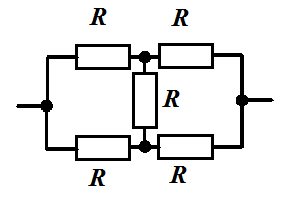
| Задача 1. 3 | Схема 1. 3 |
Определить  Потенциалы узлов а и b равны.
Сл. это
Ответ:
Потенциалы узлов а и b равны.
Сл. это
Ответ:  Проверить преобразованием треугольника в звезду
Проверить преобразованием треугольника в звезду
| 
|
| Задача 1. 4 | Схема 1. 4 |
Определить  Ответ:
Ответ: 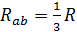
| 
|
| Задача 1. 5 | Схема 1. 5 |
| До коммутации ток в цепи 1А. Определить ток после коммутации ключа. Ответ: 1. 5А | 
|
| Задача 1. 6 | Схема 1. 6 |
| До коммутации ток в цепи 1А. Определить ток после коммутации ключа. Ответ: 3А | 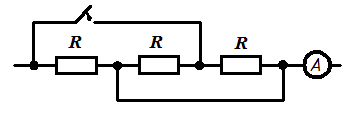
|
| Задача 1. 7 | Схема 1. 7 |
Определить  схемы в случае подключения ее к зажимам ab и ac. Сопротивление ветви каждого из участков равно R.
Ответ: схемы в случае подключения ее к зажимам ab и ac. Сопротивление ветви каждого из участков равно R.
Ответ: 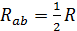
| 
|
| Задача 1. 8 | Схема 1. 8 |
Определить  (RАВ ) схемы
Ответ: (RАВ ) схемы
Ответ: 
| 
|
| Задача 1. 9 | Схема 1. 9 |
Определить 1) 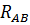 2) 2)  Сопротивление каждой ветви R
Ответ: Сопротивление каждой ветви R
Ответ:  , , 
| 
|
| Решение: 1) В силу симметрии ток в узле o отсутствует, т. е. эта точка есть точка равного потенциала | 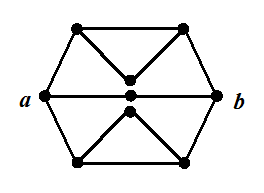
|
Решение:
2) Потенциал точек а и b одинаков. Схему можно представить как
Сопротивление ромба R. Сопротивление половины цепи вдоль c d 2R, следовательно 
| 
|
| Задача 1. 10 | Схема 1. 10 |
| Сопротивление ребра куба R. Определить 1) RАВ; 2) RАС; 3) RAD Решение: Потенциалы точек c, f, e одинаковы – это одна точка, а точки h, q, d – другая точка | 
|
|
Задача 1. 11 |
Схема 1. 11 | ||||
Решение:
Потенциалы точек c, f, e одинаковы – это одна точка, а точки h, q, d – другая точка

|
| ||||
| 2) Точки одинакового потенциала c и f, точки q и d
| 
| ||||
| Точки f и c и точки n и q имеют равные потенциалы. Эквивалентная схема. | 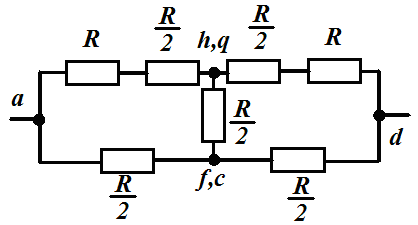
| ||||
| Узлы n, q и f, c имеют одинаковый потенциал сопротивление R/2 между ними можно не учитывать, так как ток через него не идет.
Ответ: 1) 2) | 
| ||||
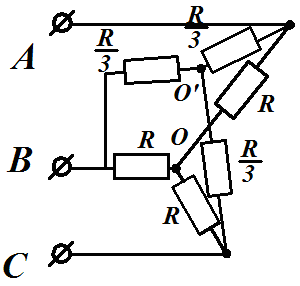
| Задача 1. 12 | Схема 1. 12. 1 |

| 
|
| Решение: В левой схеме одинаковое сопротивление по 3 Ома. Определяем радиус правой схемы, чтобы они были эквивалентными. В левой схеме преобразуем треугольник в звезду | |

| 
|
| В правой схеме преобразуем внешний треугольник в звезду. Точки О и О’ имеют одинаковый потенциал и могут быть соединены. | |
Отсюда общее сопротивление 
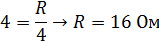
| 
|
| Второй вариант: | Схема 1. 12. 2 | |
| В правой схеме преобразуем внутреннюю звезду в треугольник и в каждом ребре треугольника получаем параллельно R и 3R. Тогда Rэкв =3/4R. Левую звезду преобразуем в треугольник с ребром 12 Ом. И из равенства 12 =3/4R получаем R = 16 Ом. | | |
|
Задача 1. 13 | Схема 1. 13 | |
Определить  . .  Ом, Ом,
 Ом Ом
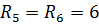 Ом, Ом,  Ом Ом
 Ом, Ом,  Ом
Ответ: Ом
Ответ: 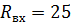
| | |
2. 8. Анализ режимов цепей постоянного тока с применением закона Ома
Алгоритм решения:
Расчет разветвленной электрической цепи, содержащей один источник энергии, целесообразно проводить с помощью закона Ома.
1. В этом случае сначала производят эквивалентное преобразование разветвленной цепи в неразветвленную, находя эквивалентное входное сопротивление относительно зажимов источника питания.
2. По найденному току источника, находят токи во всех ветвях исходной схемы.
3. Для проверки правильности расчета цепи составить уравнение энергетического баланса цепи.
| Задача 1. 15 |
Схема 1. 15 | |||
| Задана цепь и ее параметры. Определить токи. Решение. Определение токов в схеме с одним источником проводится по закону Ома, путем «сворачивания» сопротивлений с последующим распределением токов по ветвям. Найдем эквивалентное сопротивление относительно источника ЭДС |
| |||
| Сопротивление. |
Токи | |||
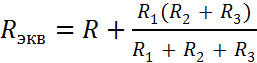
| Ток и | |||
| Задача 1. 16 |
Схема 1. 16 | |||
| Дано: E=30В, R1=5 Ом, R2=R3=20 Ом. Определить токи ветвей. |
| |||
|
Решение. | ||||
|
| ||||
|
| ||||
|
| ||||
|
| ||||
|
Составим баланс мощности Мощность источника энергии: | ||||
|
Потребляемая мощность
| ||||
|
| ||||
| Баланс имеет место. Решение верно. | ||||
|
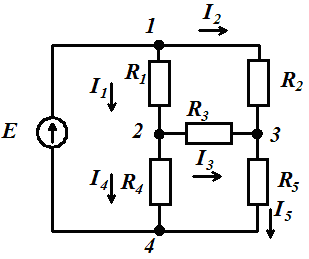
Задача 1. 17 | Схема 1. 17 | |||
| E =17 В, R1=R2=R3=R4=3 Ом, R5=5 Ом Определить токи ветвей Решение: Преобразуем треугольник (рис. а) (1, 2, 3) в звезду(1, 2, 3) (рис. б), тогда
| 
| |||
|
| 
| |||
| В исходной схеме:
| ||||
| Баланс мощности: | ||||
|
| ||||
Расчет сложных цепей на основе законов Кирхгофа методами на основе непосредственного применения законов Кирхгофа, метода контурных токов, метода узловых напряжений, метода наложения, т. е. методов предполагающих применения матричных методов решения систем линейных уравнений электрических цепей.
|
|
|






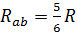
 3)
3) 


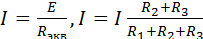
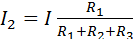






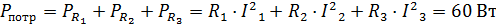


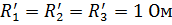 . Общий ток будет
. Общий ток будет ,
, 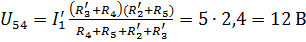


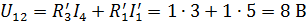

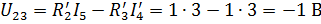


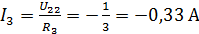
 ;
;