 |
2.5 Баланс мощностей. 2.6 Эквивалентные преобразования пассивных участков электрической цепи. 2.6.1 Последовательное соединение сопротивлений.
|
|
|
|
2. 5 Баланс мощностей
При протекании токов по сопротивлениям в них выделяется теплота. На основании закона сохранения энергии количество теплоты, выделяющееся в единицу времени в сопротивлениях цепи, должно равняться энергии, доставляемой за то же время источником питания. Если направление тока I, протекающего через источник ЭДС E, совпадает с направлением ЭДС, то источник ЭДС доставляет в цепь энергию в единицу времени, равную EI, и произведение ЕI входит в уравнение энергетического баланса с положительным знаком. Если же направление тока I встречно ЭДС Е, то источник ЭДС не поставляет энергию, а потребляет ее (например, заряжается аккумулятор), и произведение ЕI войдет в уравнение энергетического баланса с отрицательным знаком. Уравнение энергетического баланса при питании только от источников ЭДС имеет вид
 . .
| (1. 15) |
В случае питания электрической цепи не только источниками ЭДС, но и источниками тока, при составлении уравнения энергетического баланса необходимо учесть и энергию, доставляемую источниками тока. Предположим, что к узлу а схемы подтекает ток J от источника тока, а от узла b этот ток утекает. Доставляемая источником тока мощность равна UаbJ. Общий вид уравнения энергетического баланса:
 . .
| (1. 16) |
2. 6 Эквивалентные преобразования пассивных участков электрической цепи
Расчет разветвленной электрической цепи, содержащей один источник энергии, целесообразно производить с помощью закона Ома.
В этом случае прежде производят эквивалентное преобразование разветвленной цепи в неразветвленную, находя эквивалентное сопротивление пассивной части цепи относительно зажимов источника питания (рис. 2. 4, а, б).
|
|
|

| 
|
| а) | б) |
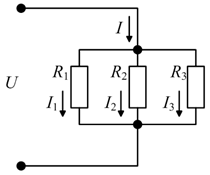
| Рис. 1. 6 Соединение сопротивлений: последовательное (а); параллельное (б) | |
2. 6. 1 Последовательное соединение сопротивлений.
При последовательном соединении сопротивлений эквивалентное сопротивление равно сумме этих сопротивлений. Пример (рис. 1. 6, а)
Второй закон Кирхгофа для этой схемы имеет вид U = U1 + U2 + U3. Поделим это уравнение на ток I:
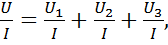 или R = R1+ R2+ R3. или R = R1+ R2+ R3.
| (1. 17) |
Таким образом, при последовательном соединении сопротивлений эквивалентное сопротивление равно сумме последовательно соединенных  .
.
2. 6. 1 Параллельное соединение сопротивлений.
При параллельном соединении сопротивлений суммируются проводимости. Например для преобразования схемы
(рис. 1. 6, б) используя первый закон Кирхгофа и закон Ома.

| (1. 18) |

| (1. 19) |
Отсюда следует, что
 
| (1. 20) |
Таким образом, при параллельном соединении сопротивлений эквивалентная проводимость равна сумме проводимостей, откуда эквивалентное сопротивление имеет вид:
RЭ=  . .
| (1. 21) |
При параллельном соединении двух одинаковых сопротивлений R эквивалентное сопротивление будет R/2, трех сопротивлений – R/3 и т. д. ‘
При смешанном соединении в цепи есть участки разных соединений.
2. 6. 2 Соединение звездой и треугольником.
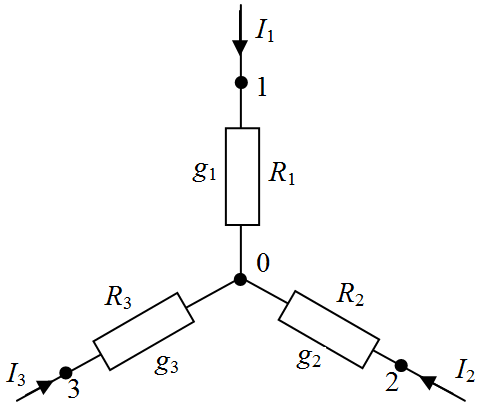
Из равенства сопротивлений в обеих схемах между двумя узлами при разомкнутом третьем легко выводятся выражения для преобразование звезда – треугольник (рис. 1. 7, а),
 ,
,

| 
|
| а) | б) |
|
| |
| Рис. 1. 7. Соединение сопротивлений при преобразовании равностороннего треугольника (а) в звезду (б) | |
для преобразование треугольник – звезда (рис. 2. 5, б)
 .
.
При преобразовании равностороннего треугольника в звезду у последней сопротивления будут в три раза меньше и наоборот (рис. 1. 7, в).
|
|
|


