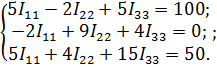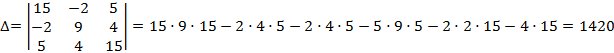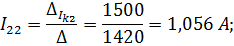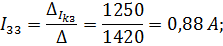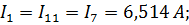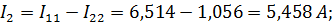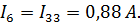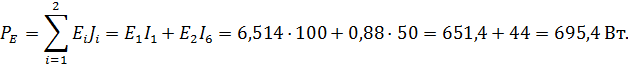2.10. Метод законов Кирхгофа.   2.11. Метод контурных токов. Алгоритм решения. Решение. Задача 1.21. Алгебраическая сумма напряжений на элементах контура равна алгебраической сумме ЭДС, действующих в этом же контуре

2. 10. Метод законов Кирхгофа

Режимы электрических цепей определяются первым и вторым законами Кирхгофа.

Первый закон Кирхгофа. Для цепи постоянного тока:

Алгебраическая сумма токов в узле равна нулю.

.

(1. 30)

Второй закон Кирхгофа:

Алгебраическая сумма напряжений на элементах контура равна алгебраической сумме ЭДС, действующих в этом же контуре

Для цепи постоянного тока

.

(1. 31)

Алгоритм решения:

1. Выбрать произвольно положительные направления искомых токов ветвей. Число токов должно быть равно числу ветвей схемы без учета ветвей, содержащих источники тока.  

2. Составить у - 1 уравнений по первому закону Кирхгофа, где у – число узлов схемы. В алгебраической сумме следует учесть и токи источников тока, связанные с соответствующими узлами.

3. Составить уравнения по второму закону Кирхгофа для независимых контуров. Независимые контуры отличаются друг от друга хотя бы одной ветвью. Необходимо учесть, что при выборе контуров, ветви с источниками тока исключаются. Выбрать положительные направления обхода контуров. Составить уравнения по следующему правилу: если направление тока ветви и направление обхода контура совпадают, напряжение на участке записать со знаком плюс, в противном случае со знаком минус. Аналогично выбирают знак ЭДС.

4. Общее количество уравнений должно быть равно числу ветвей схемы без учета ветвей, содержащих источники тока. Подставить численные значения и решить систему уравнений.

5. Проверить правильность полученного решения с помощью уравнения баланса мощность цепи.

Задача 1. 18	Схема 1. 18
Дано: E1=36B; E2=12B; J=8A; R1=R2=4Ом; R3=1 Ом; R4=3 Ом.    Определить токи ветвей.
Решение.	В схеме 5 ветвей и 3 узла.
По первому закону Кирхгофа можно составить 2 независимых уравнения:
В качестве независимых контуров выбираем:
Выбираем обход контуров по часовой стрелке
		Полная система уравнений   или
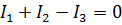
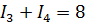
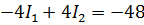
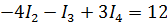
Токи в ветвях:
Составляем уравнение баланса мощности цепи.
Подставляем числовые значения		408 Вт = 408 Вт.
Баланс мощности имеет место, следовательно, полученное решение верно.

 

 

Задача 1. 19	Схема 1. 19
Дано: E1=50 B; E2=400 B; R1=50 Ом; R2=20 Ом; R3=50 Ом; R4=80 Ом.    Определить токи ветвей.
Решение.
1 контур 2 контур
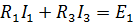
	Решение:
Подставим численные значения:
Генерируемая мощность = 1200 Вт.		Потребляемая = 1200 Вт.
Источник энергии Е1 работает в режиме генератора
Источник энергии Е2 – потребитель энергии.
Баланс мощности 1200 Вт = 1200 Вт. Решение верно.

                          2. 11. Метод контурных токов

 

Метод контурных токов основан на введении промежуточных неизвестных переменных – контурных токов.

Контурных ток – условный ток каждого независимого контура.

Введение контурных токов позволяет уменьшить количество уравнений, составляемых для расчета цепи. Уравнения составляются по второму закону Кирхгофа и поэтому их число равно количеству независимых контуров. Токи ветвей определяются алгебраическим суммированием контурных токов.

Алгоритм решения.

1. Выбрать в расчетной схеме независимые контуры и поставить произвольно положительные направления контурных токов в схеме.

Примечания.

При наличии в схеме источника тока:

 - либо преобразовать его в источник ЭДС;

 - либо добавить к выбранным контурам еще один контур с ветвью, содержащей источник тока. Контурный ток этого контура известен и равен току источник тока.

2. Для каждого независимого контура составить контурное уравнение на основании второго закона Кирхгофа.

(1. 32)

- сопротииление к-го контура;

= - сопротивление общей ветви к и m контуров;

 – суммарная Э. Д. С. к-го контура.

3. объединив полученные контурные уравнения в систему линейных алгебраических уравнений и подставив численные заданные значения параметров, решить систему и найти контурные токи.

4. используя полученные контурные токи, определить действительные токи ветвей, для чего:

 - выбрать произвольно положительные направления токов ветвей, показать их на схеме

- искомые токи внешних ветвей равны соответствующим контурным токам;

 - в смежных между контурами ветвях искомые токи равны алгебраическим суммам соответствующих контурных токов в данной ветви.

5. Проверить правильность полученного решения с помощью уравнения баланса мощность цепи.

Задача 1. 20	Схема 1. 20
Дано: E1=36B; E2=12B; J=8A; R1=R2=4 Ом; R3=1 Ом; R4=3 Ом. Определить токи ветвей.
Решение.
Независимых контуров два	Контурные токи I11 и I22
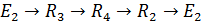
Добавлен третий контур, в который входит ветвь с током источника тока J
Его контур ток I33 =J=8 A

 

Контурные уравнения цепи:
Решение системы уравнений:
Дает ответ: I11=-9A; I22=-6A.
Обозначим на схеме произвольно выбранный положительные направления токов ветвей и найдем эти токи.
Составим уравнение баланса мощности.
Мощность источников энергии:
Мощность потребителей:
Баланс мощности имеет место, расчет верен.

 

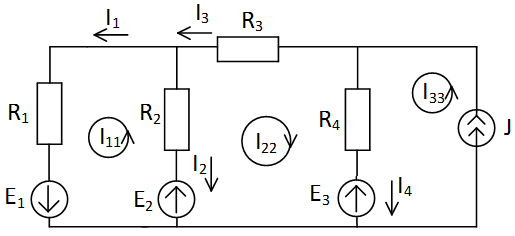
Задача 1. 21			Схема 1. 21
Дано: E1=20 B; E2=5B; E3=35 B; R1=10 Ом; R2=R3=5 Ом; R4=15 Ом; R5=5 Ом. Определить токи ветвей.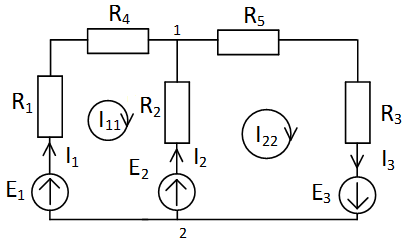
Решение.
Контурные уравнения цепи:
Решение системы уравнений:
	Контурные токи
Составим уравнение баланса мощности.
		Баланс мощности имеет место, расчет верен.

 

 

Задача 1. 22				Схема 1. 22
Дано: E1=20 B; E2=5B; E3=35 B; R1=10 Ом; R2=R3=5 Ом; R4=15 Ом; R5=5 Ом. Определить токи в ветвях.
Решение.
Применяем метод контурных токов.							Независимых контуров два.
Добавлен третий контур с источником тока с током I33 = J = 8A
Уравнения цепи:					R11 = R1+R2=8; R22=R2+R3+R4=8; R12=R21=-R2= -4
Решение системы уравнений:						Отсюда токи:
Произвольно выберем направление токов ветвей и найдем их.
Ответ:

 

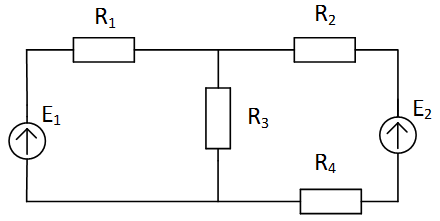
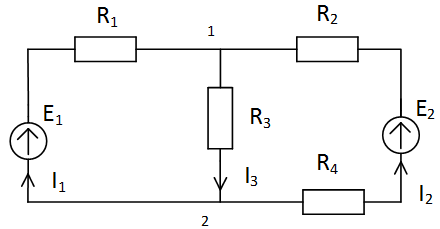
Задача 1. 23		Схема 1. 23
Расчет сложных электрических цепей постоянного тока методом контурных токов. Для сложной электрической схемы, для которой заданы значения напряжений ЭДС и сопротивлений резисторов.
Требуется определить токи в цепи, составить баланс мощностей. В основе метода лежит введение в каждый контур условного контура тока, направление которого обычно выбирают совпадающим с направлением обхода контура. Для тока контур верны законы Кирхгофа.
Уравнения контурных токов следующие:	.

 

 

При подстановке значений сопротивлений и ЭДС уравнения обретают вид:
Определитель системы
Определители токов
Контурные токи
Токи в резисторах схемы:
Падение напряжения на каждом резисторе, вычисляется как: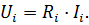
Мощность, выделяемая на каждом резисторе, вычисляется как: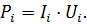
Баланс мощностей. Мощность на резисторах и отдаваемая источником ЭДС
Баланс мощности имеет место, расчет верен.

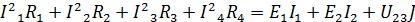
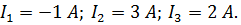
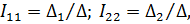
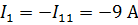
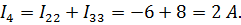
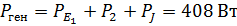
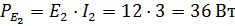
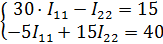
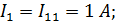
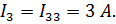
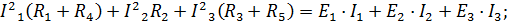
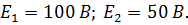
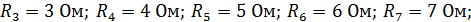
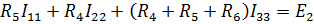⇐ Предыдущая45678910111213Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: