 |
Решение. 1. Метод обратной матрицы.
|
|
|
|
Решение. 1. Метод обратной матрицы.
Введем обозначения:
, 
, 
.
Тогда в матричной форме данная система имеет вид: 
. Умножим слева обе части матричного равенства на обратную матрицу 
, получим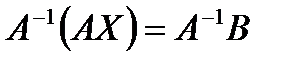 
. Так как 
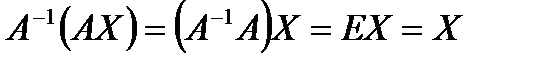, то решением системы методом обратной матрицы будет матрица-столбец
 .
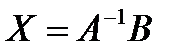| (1. 1) |
Найдем матрицу .
Вычислим определитель матрицы А, применяя, например, формулу
 .
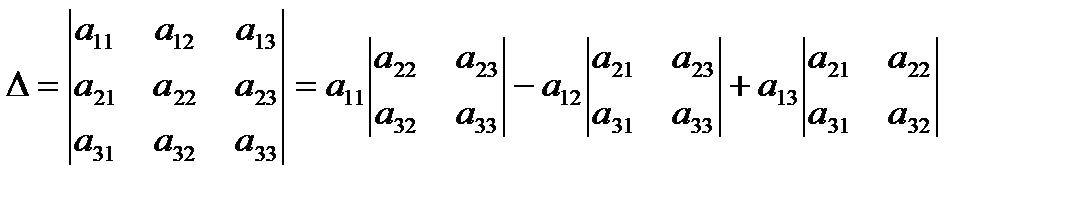| (1. 2) |
,
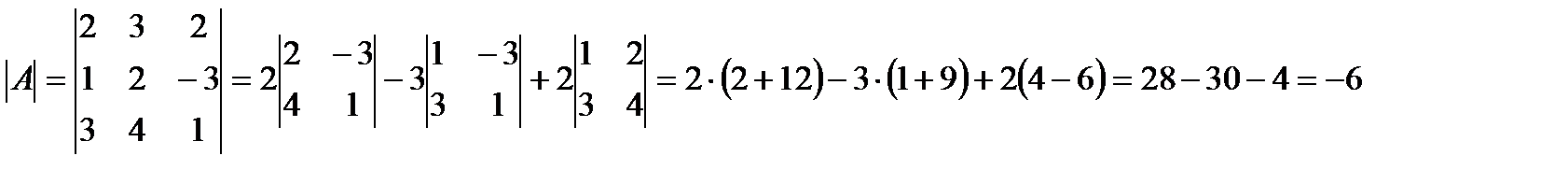, следовательно, обратная матрица 
существует.
Вычисляем алгебраические дополнения ко всем элементам матрицы 
:
, 
, 
,
, 
, 
,
, 
, 
.
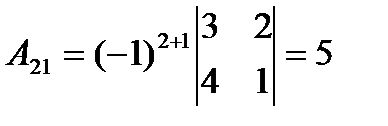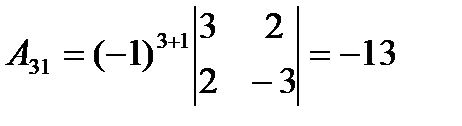Составляем матрицу 
:
.
Транспонируем матрицу :
.
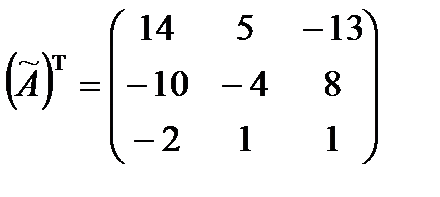Находим обратную матрицу:
.
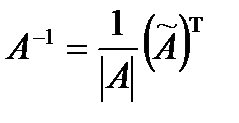
Тогда по формуле (1. 1)
,
то есть решение системы: 
.
2. Метод определителей (метод Крамера).
Найдем определитель системы 
(см. п. 1). Так как 
, то по теореме Крамера система имеет единственное решение.
Вычислим определители матриц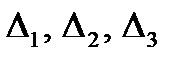 
, полученных из матрицы 
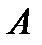, заменой соответственно первого, второго и третьего столбцов столбцом свободных членов:
, 
, 
.
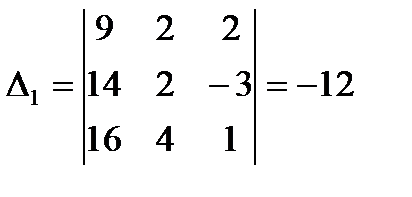Решение системы находим по формулам:
, 
, 
,
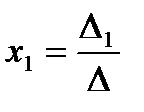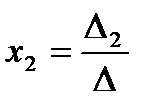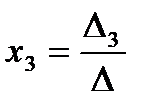откуда получаем
.
3. Метод Гаусса.
Замечание 1. 1. Напомним, что метод Гаусса заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.
Преобразования Гаусса удобнее проводить не с самими уравнениями системы, а с матрицей их коэффициентов, то есть со строками расширенной матрицы системы.
К элементарным преобразованиям относятся:
1) перестановка местами двух строк матрицы;
2) умножение всех элементов строки на число, отличное от нуля;
|
|
|
3) прибавление к элементам одной строки соответствующих элементов другой строки, умноженных на одно и то же число.
Расширенная матрица исходной системы имеет вид
.
Для удобства преобразований, поменяем в расширенной матрице первую и вторую строки:
.
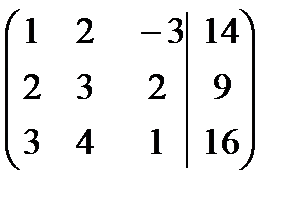Далее умножаем первую строку на 
и прибавляем ко второй строке, потом умножаем первую строку на 
и прибавляем её к третьей строке. Третью строку полученной матрицы поделим на :
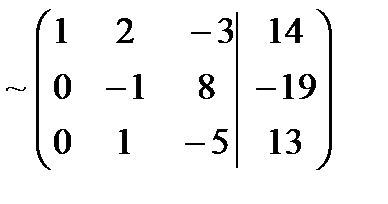
Вторую строку последней матрицы прибавляем к третьей, в результате получим
.
Запишем систему уравнений, соответствующую преобразованной матрице коэффициентов:
.
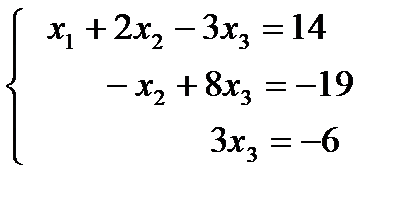Из последнего уравнения находим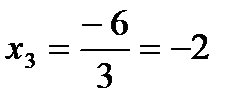 
; подставляем найденное значение 
во второе уравнение системы: 
, 
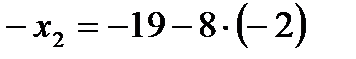, и из первого уравнения: 
, 
.
Таким образом, решение системы: .
Задача 1. Решить систему линейных алгебраических уравнений: 1) методом обратной матрицы; 2) методом определителей; 3) методом Гаусса.
1. 1.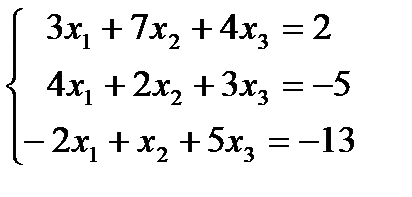 
| 1. 2.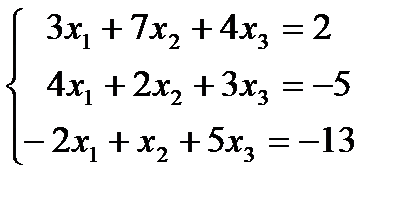 
|
1. 3. 
| 1. 4.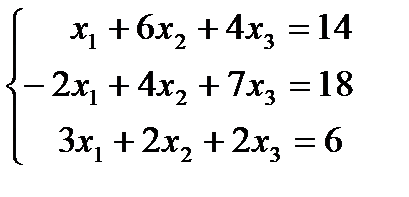 
|
1. 5.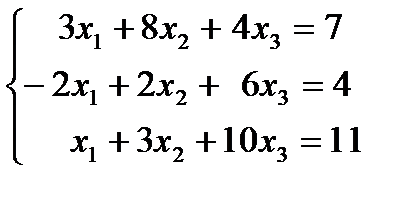 
| 1. 6.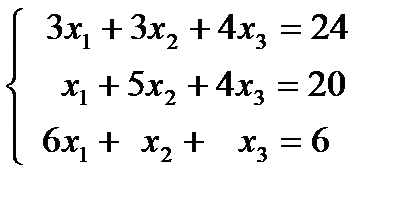 
|
1. 7. 
| 1. 8.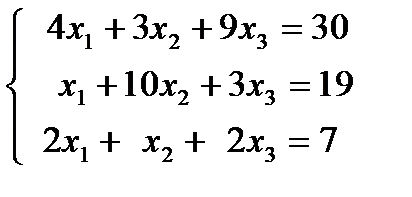 
|
1. 9. 
| 1. 10. 
|
1. 11. 
| 1. 12. 
|
1. 13. 
| 1. 14. 
|
1. 15. 
| 1. 16.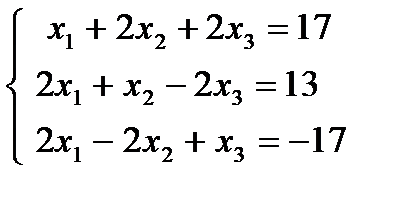 
|
1. 17. 
| 1. 18. 
|
1. 19. 
| 1. 20. 
|
1. 21.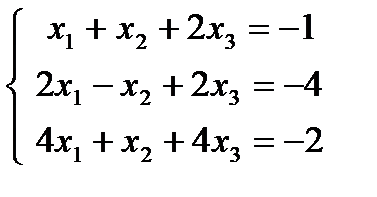 
| 1. 22. 
|
1. 23.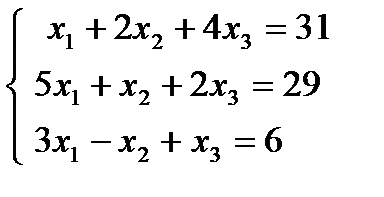 
| 1. 24.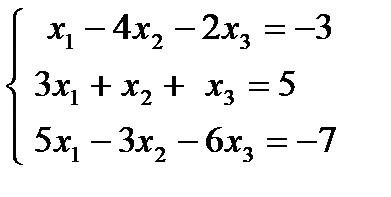 
|
1. 25.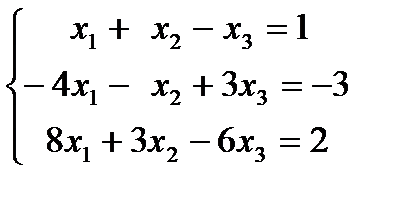 
| 1. 26. 
|
1. 27. 
| 1. 28. 
|
1. 29. 
| 1. 30. 
|
2. ЛИНЕЙНЫЕ ЭЛЕКТРИЧЕСКИЕ ЦЕПИ ПОСТОЯННОГО ТОКА
2. 1 Электрическая цепь. Двухполюсники. Цепи линейные и нелинейные
Простейшая электрическая цепь состоит из источника электрической энергии, приемника и соединительных проводов. Условное графическое изображение цепи называют схемой.
Согласно закону Ома, ток в цепи (рис 1. 1а)
| I = E/(R+Ri), | (1. 1) |
где Е – ЭДС источника; R – сопротивление приемника; Ri – внутреннее сопротивление источника.
По количеству полюсов источник и приемник являются двухполюсниками. Первый из них – активный двухполюсник (в нем есть ЭДС), второй – пассивный.
Зависимость тока в двухполюснике от напряжения называется вольтамперной характеристикой. Для пассивного двухполюсника
|
|
|
| U = RI. | (1. 2) |
Формуле (1. 2) соответствует прямая, выходящая из начала координат.
Вольтамперная характеристика активного двухполюсника получается из равенства (1. 1):
| U = E - RiI. | (1. 3) |
Её можно построить по двум точкам: при I = 0 напряжение U = E, при U = 0 ток короткого замыкания Iк = E/Ri. (Рис. 1. 1б, 1. 2б)
Вольтамперные характеристики могут быть линейными и нелинейными. Соответственно характеристикам все двухполюсники, а затем и цепи подразделяются на линейные и нелинейные.
Линейная цепь состоит только из линейных двухполюсников. Если в ней есть хоть один нелинейный элемент, она нелинейна.
Расчет линейных цепей значительно проще, чем нелинейных. Поэтому при решении многих задач изменением сопротивлений пренебрегают и считают цепи линейными, состоящими из идеальных линейных двухполюсников.
Энергию двухполюсников вычисляют по закону Джоуля – Ленца:
| W = RI2t; W = EIt. |
(где t – время), а мощность – по формулам:
| P = RI2; P = EI. |
|
|
|
