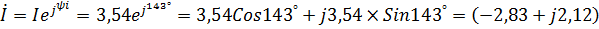|
Задача 2.1. Решение задачи 2.1. Представить напряжение в виде: 1) тригонометрической функции времени; 2) комплексного числа; 3) вектора на комплексной плоскости
|
|
|
|
Задача 2. 1
|
| Синусоидальное напряжение задано в виде графика мгновенных значений: Um=20 В; Т=0, 002 с; U(0)=10 В. | ||
| Представить напряжение в виде: | |||
|
Решение задачи 2. 1 | |||
| 1. Для представления синусоидаль-ного напряжения в виде тригоно-метрической функции времени | - угловую частоту - начальную фазу | ||
|
необходимо определить: | Тогда: | ||
| 2. Комплексная амплитуда напряжения:
| |||
| Комплекс действующего значения напряжения: 3. Комплекс действующего значения напряжения на комплексной плоскости: | 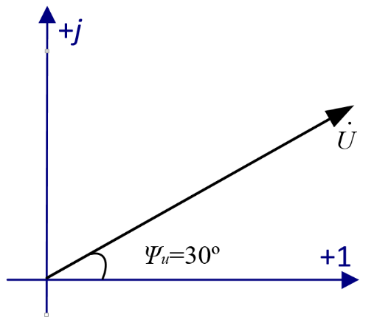
| ||
Задача 2. 2
| Синусоидальный ток, заданный графиком мгновенных значений, представить в виде: |
| |
| 1) тригонометрической функции времени; | ||
|
Решение задачи 2. 2. | ||
| 1. Так как | ||
| Начальная фаза | ||
| Тогда ток в тригонометрической форме: | 
| |
|
| 
| |
|
| ||
Определение: Совокупность векторов на комплексной плоскости построенных с соблюдением правильной ориентации их относительно друг друга и отображающих процессы, происходящие в цепях называется векторной диаграммой.
Анализ электрических цепей переменного тока производится, комплексным методом.
Идея комплексного метода заключается в замене мгновенных значений синусоидально изменяющихся ЭДС, напряжений и токов, действующих в расчетной схеме, на изображающие их комплексные ЭДС, напряжения, токи:
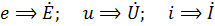
Параметры (сопротивление R, индуктивность L, емкость C) пассивных элементов схемы (резисторов, катушек индуктивности, конденсаторов) также заменяют их комплексными изображениями, которые учитывают сопротивления, оказываемые ими синусоидальному току, а также вносимый ими сдвиг по фазе между приложенным к этим элементам напряжениям и протекающим по ним токам:
|
|
|

Интегро-дифференциальные уравнения, описывающие режимы в цепях синусоидального тока  , при изображении токов и напряжений в виде комплексов и введении комплексных сопротивлений превращаются в алгебраические, что значительно упрощает расчет цепей.
, при изображении токов и напряжений в виде комплексов и введении комплексных сопротивлений превращаются в алгебраические, что значительно упрощает расчет цепей.
Закон Ома для участка цепи: 
где 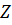 - комплексное сопротивление участка; Y- комплексная проводимость участка.
- комплексное сопротивление участка; Y- комплексная проводимость участка.
1 - й закон Кирхгофа: 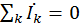
2 - й закон Кирхгофа: 
Алгоритм перехода к комплексному методу
1. Заменить мгновенные значения ЭДС, напряжений и токов расчетной схемы на их комплексные изображения.
2. Заменить параметры пассивных элементов.
3. Рассчитать одним из методов расчета цепей комплексные значения искомых величин.
4. При необходимости перейти к мгновенным значениям искомых величин.
3. 3. Комплексное сопротивление и проводимость. Законы Ома
и Кирхгофа в комплексной форме. Векторные
топографические диаграммы
Рассмотрим участок цепи при последовательном соединении активного сопротивления, индуктивности и конденсатора (рис. 2. 7). В схеме протекает синусоидальный ток 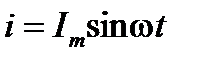 .
.
Рис. 2. 7
В соответствии со вторым законом Кирхгофа (2. 7) уравнение для мгновенных значений напряжений:
 ; (2. 13)
; (2. 13)
 . (2. 14)
. (2. 14)
Подставим выражения (2. 14) в уравнение (2. 13). Получим:
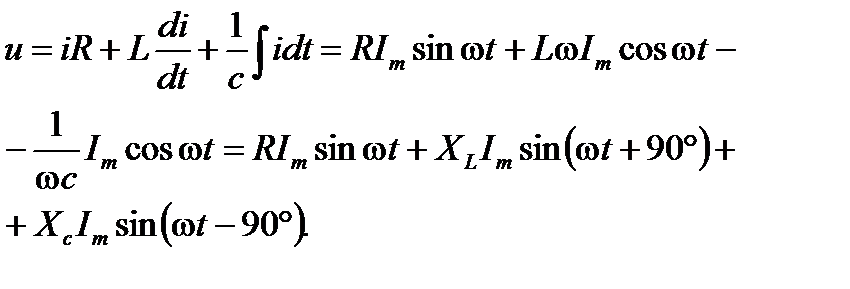 (2. 15)
(2. 15)
Из выражения (2. 15) следует, что напряжение в активном сопротивлении совпадает по фазе с током, напряжение на индуктивности опережает по фазе ток на 90o, напряжение по емкости отстает по фазе от тока на 90o.
Запишем уравнение (2. 15) в комплексной форме:
|
|
|
 (2. 16)
(2. 16)
Получим уравнение для комплексов действующих значений токов и напряжений, разделив члены (2. 16) на 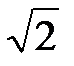 :
:
 .
.
Отсюда закон Ома для RLC цепи в комплексной форме
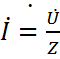 (2. 17) , где Z – комплексное сопротивление цепи
(2. 17) , где Z – комплексное сопротивление цепи
Откуда (2. 17) отношение комплексного напряжения к комплексу тока
 . (2. 18)
. (2. 18)
Точку только над комплексными величинами, отображающими синусоидальные функции времени. Комплексное число Z (2. 18) может быть представлено в показательной или алгебраической форме:
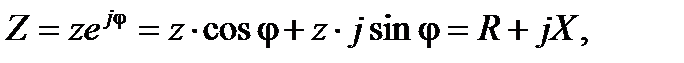 (2. 19)
(2. 19)
где z- модуль комплексного сопротивления или полное сопротивление цепи;
φ - аргумент комплексного сопротивления,  - соответственно активное и реактивное сопротивление.
- соответственно активное и реактивное сопротивление.
Для рассматриваемой схемы (рис. 2. 9) данные величины равны:
φ =arctg  ,
, 
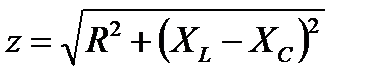 ,
,
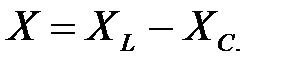 (2. 20)
(2. 20)
Знак величины реактивного сопротивления X и аргумента (фазы) 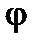 зависит от соотношения индуктивного и емкостного сопротивлений.
зависит от соотношения индуктивного и емкостного сопротивлений.
При построении векторных диаграмм цепи возможны три режима.
1. Индуктивное сопротивление больше емкостного, величина реактивного сопротивления X и аргумента φ положительны. Цепь носит индуктивный характер. Векторы напряжений на индуктивности и емкости направлены в противоположные стороны, частично компенсируют друг друга. Вектор тока отстает от вектора напряжения на входе схемы (рис. 2. 8).
2. Индуктивное сопротивление меньше емкостного, величина реактивного сопротивления X и аргумента φ отрицательны. Цепь носит емкостной характер. Вектор тока опережает вектор напряжения на входе схемы (рис. 2. 9).
3. Индуктивное и емкостное сопротивления одинаковы. Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения (рис. 2. 10), который рассматривается в п. 2. 6.

Рис. 2. 8 Рис. 2. 9 Рис. 2. 10
В ветвях цепи при параллельном соединении активного сопротивления, индуктивности и конденсатора (рис. 2. 11) удобнее выполнять расчеты с использованием комплексной проводимости.
|
|
|
|
|
|




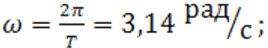
 .
. 
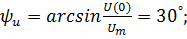
 B.
B.  B.
B. 
 , то
, то