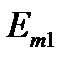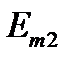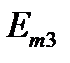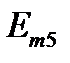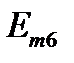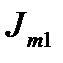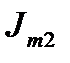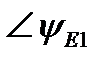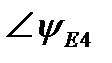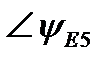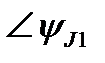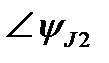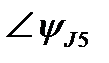3.8. Самостоятельная работа. Приложения. Приложение 1. Резонансные режимы в цепи. Резонанс напряжения, резонанс

3. 8. Самостоятельная работа

Задание. Расчет цепей по комплексным значениям

На рисунке 1 приведена схема электрической цепи, состоящая из шести обобщенных ветвей, каждая из которых содержит источник тока J, источник напряжения E, и комплексное сопротивление Z.  Используя данные таблицы 1 и 2, составить расчетную схему, соответствующую заданному варианту. Применяя метод контурных токов для комплексных амплитуд, выполнить следующее:

1) определить амплитуды токов во всех ветвях схемы;

2) определить напряжения на всех элементах внешнего контура;

3) составить баланс активных и реактивных мощностей;

4) построить векторную диаграмму токов цепи;

5) построить векторную диаграмму для напряжений внешнего контура.

Параметры пассивных элементов схемы приведены в таблице 1 и параметры источников в таблице 2.

 

Рис. 1

 

Таблица 1

Параметры элементов цепи

 

 

Таблица 2

Параметры источников напряжения и тока

рад/с

14, 5

5, 5

∠ 0°

∠ -55°

∠ 70°

16, 5

4, 25

∠ -75°

∠ 0°

∠ 90°

18, 5

3, 75

∠ 85°

∠ -25°

∠ 0°

20, 5

∠ 0°

∠ 40°

∠ -55°

22, 5

1, 5

∠ 60°

∠ 0°

∠ -75°

5, 25

∠ -80°

∠ 10°

∠ 0°

4, 75

∠ 0°

∠ 25°

∠ -40°

∠ 45°

∠ 0°

∠ -60°

24, 5

5, 5

∠ 80°

∠ -10°

∠ 0°

∠ 0°

∠ -10°

∠ 25°

19, 5

5, 75

∠ 30°

∠ 0°

∠ -45°

21, 5

∠ 50°

∠ -65°

∠ 0°

4, 5

∠ 75°

∠ 0°

∠ -90°

10, 5

∠ -15°

∠ 0°

∠ 30°

12, 5

1, 5

∠ -35°

∠ 50°

∠ 0°

∠ 0°

∠ 55°

∠ -70°

23, 5

3, 5

∠ 0°

∠ 70°

∠ -85°

∠ -20°

∠ 35°

∠ 0°

2, 5

∠ 0°

∠ -40°

∠ 55°

1, 25

∠ -60°

∠ 0°

∠ 75°

2, 5

∠ 65°

∠ -80°

∠ 0°

11, 5

∠ 0°

∠ -25°

∠ -40°

13, 5

3, 5

∠ -45°

∠ 0°

∠ 60°

15, 5

1, 25

∠ -65°

∠ 80°

∠ 0°

17, 5

1, 75

∠ 0°

∠ -85°

∠ 15°

∠ -30°

∠ 0°

∠ 45°

∠ 35°

∠ -50°

∠ 0°

2, 75

∠ -90°

∠ 0°

∠ 20°

3, 25

∠ 0°

∠ -70°

∠ 85°

7, 5

∠ -50°

∠ 65°

∠ 0°

Приложения

Приложение 1

Резонансные режимы в цепи. Резонанс напряжения, резонанс

токов

 Реактивные сопротивления и проводимости отдельных участков цепи могут быть положительными (индуктивные элементы) и отрицательными (емкостные элементы). Поэтому возможны такие сочетания этих элементов, когда входное реактивное сопротивление или входная реактивная проводимость всей цепи равны нулю. При этом ток и напряжение на входе цепи совпадают по фазе и эквивалентное сопротивление всей цепи является активным. Такие режимы цепи называются резонансными.

Резонанс напряжений. На рис. 2. 7 приведена цепь, включающая последовательно соединенные активное сопротивление, индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда индуктивное и емкостное сопротивления одинаковы по величине (рис. 2. 10). Напряжения на индуктивности и емкости полностью компенсируют друг друга. Ток в цепи совпадает по фазе с входным напряжением. В электрической цепи наступает режим резонанса напряжения.

Ток в резонансном режиме достигает максимума, так как полное сопротивление z цепи имеет минимальное значение:  

                                    .

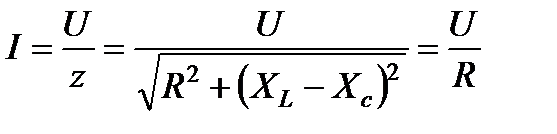Условие возникновения резонанса: .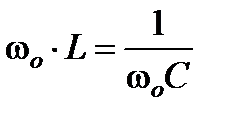

 Частоту называют резонансной частотой:

      .                                    

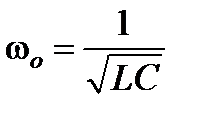В резонансном режиме входное напряжение равно падению напряжения в активном сопротивлении. На индуктивности и емкости схемы могут возникнуть напряжения, значительно превышающие напряжение на входе цепи, если реактивные сопротивления значительно превышают активное сопротивление. Напряжение на индуктивности при резонансе равно напряжению на емкости:

.

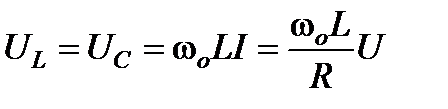Отношение 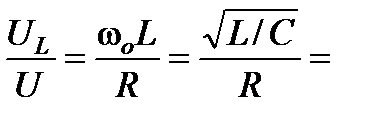    Q называют добротностью контура.

Добротность показывает, во сколько раз напряжения на реактивных элементах превышают входное напряжение в резонансном режиме. В радиотехнических цепях добротность составляет несколько сотен. Резонансные свойства характеризуют также величиной обратной добротности 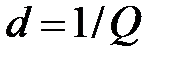, называемой затуханием контура.

Волновое сопротивление контура или характеристическое сопротивление  определяет отношение напряжения на реактивных элементах в резонансном режиме к величине тока:

.

Резонанс токов. На рис. 2. 11 приведена цепь, включающая параллельно соединенные активное сопротивление, идеальная индуктивность и емкость. При построении векторных диаграмм этой цепи рассмотрен режим, когда реактивная проводимость цепи (рис. 2. 14). При этом индуктивный и емкостный токи, направленные в противоположные стороны, полностью компенсируют друг друга. Ток в неразветвленной части схемы совпадает по фазе с напряжением. В электрической цепи наступает режим резонанса токов.

Из условия возникновения резонанса тока получим формулу для резонансной частоты тока:

.

 

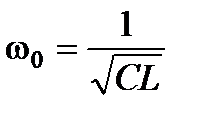В режиме резонанса тока полная (входная) проводимость цепи 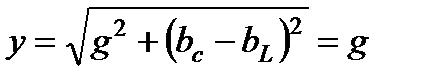- минимальна, а полное сопротивление  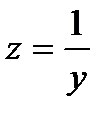- максимально. Ток в неразветвленной части схемы  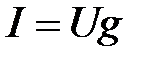в резонансном режиме имеет минимальное значение, в отличие от резонанса напряжений, когда ток имеет максимальное значение. В идеализированном случае при R = 0,

и .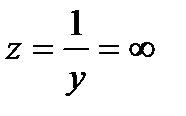

Ток в неразветвленной части цепи I = 0. Такая схема называется фильтр - пробкой.

При резонансе токов возможны режимы, когда токи через индуктивность и емкость значительно превосходят ток в неразветвленной части схемы. Превышение токов в реактивных элементах над током в неразветвленной части схемы имеет место при условии

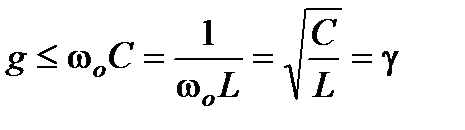
Величина   имеет размер проводимости и называется волновой проводимостью контура.

Добротность контура Q при резонансе токов определяет кратность превышения тока в индуктивности и емкости 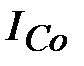над током в неразветвленной части схемы :

 

.

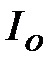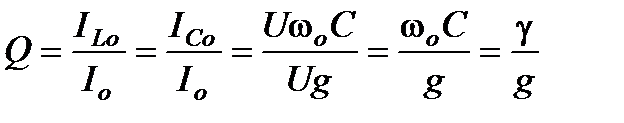Величина обратная добротности  является затуханием контура.

Важной характеристикой контура является его полоса пропускания

,

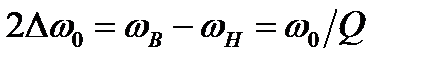которая характеризует избирательные свойства контура. Из этого выражения следует, что с повышением добротности контура его полоса пропускания уменьшается. Относительная полоса пропускания

,

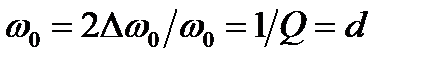где  — затухание контура.

 

⇐ Предыдущая11121314151617181920Следующая ⇒

Поделиться:

Воспользуйтесь поиском по сайту: