 |
Декартова система координат в пространстве.
|
|
|
|
Декартовы координаты в пространстве задаются с помощью точки начала координат и трёх взаимно-перпендикулярных направленных прямых. Прямые занумерованы, задан единичный отрезок. Положение любой точки в пространстве однозначно определено тремя числами: первое число – величина проекции точки на первую ось, второе – величина проекции на вторую ось, третье – на третью.

Билет 9.
Прямая на плоскости. Различные формы уравнения прямой. Простейшие задачи.
| Прямая на плоскости |
Пусть  – заданная точка на прямой – заданная точка на прямой  , ,  – вектор, перпендикулярный прямой – вектор, перпендикулярный прямой  , его называют нормальным вектором прямой, и пусть , его называют нормальным вектором прямой, и пусть  – произвольная точка прямой – произвольная точка прямой  (рис. 20). Тогда (рис. 20). Тогда  , ,  , то есть , то есть
 . (2.12)
(2.12) – уравнение прямой, проходящей через данную точку перпендикулярно данному вектору. . (2.12)
(2.12) – уравнение прямой, проходящей через данную точку перпендикулярно данному вектору.
 Рис. 20
Раскрыв скобки и сгруппировав слагаемые в (2.12), получим
Рис. 20
Раскрыв скобки и сгруппировав слагаемые в (2.12), получим  . Обозначим . Обозначим  , уравнение примет вид , уравнение примет вид
 . (2.13)
(2.13) – общее уравнение прямой на плоскости.
Если в уравнении (2.13) . (2.13)
(2.13) – общее уравнение прямой на плоскости.
Если в уравнении (2.13)  , ,  , ,  , то, перенеся слагаемое С в правую часть и разделив на него обе части уравнения, получим , то, перенеся слагаемое С в правую часть и разделив на него обе части уравнения, получим
 , или , или  . Обозначим . Обозначим  , ,  , тогда уравнение примет вид , тогда уравнение примет вид
 (2.14)
(2.14) – уравнение прямой в отрезках, здесь a и b – отрезки, отсекаемые прямой на осях координат (рис. 21): из уравнения (2.13) при (2.14)
(2.14) – уравнение прямой в отрезках, здесь a и b – отрезки, отсекаемые прямой на осях координат (рис. 21): из уравнения (2.13) при  получим получим 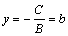 , а при , а при   . .
 Рис. 21
Пусть
Рис. 21
Пусть  – заданная точка на прямой – заданная точка на прямой  , ,  – вектор, параллельный прямой, его называют направляющим вектором прямой, и пусть – вектор, параллельный прямой, его называют направляющим вектором прямой, и пусть  – произвольная точка прямой – произвольная точка прямой  (рис. 22). Тогда (рис. 22). Тогда
 , ,   . (2.15)
(2.15) – каноническое уравнение прямой, или уравнение прямой, проходящей через данную точку параллельно данному вектору.
. (2.15)
(2.15) – каноническое уравнение прямой, или уравнение прямой, проходящей через данную точку параллельно данному вектору.
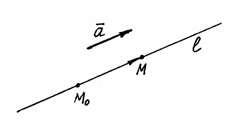 Рис. 22
В частности, если прямая
Рис. 22
В частности, если прямая  параллельна оси параллельна оси  , то ее направляющий вектор , то ее направляющий вектор  , и каноническое уравнение имеет вид , и каноническое уравнение имеет вид  , или , или  . Если . Если  , то , то  , и каноническое уравнение прямой , и каноническое уравнение прямой  , или , или  .
Если в уравнении (2.15) величину отношения положить равной .
Если в уравнении (2.15) величину отношения положить равной  ( (  – параметр, переменная величина, – параметр, переменная величина,  ): ):
 , ,  , то, выразив , то, выразив  и и  из уравнений, получим из уравнений, получим
 , ,  . (2.16)
(2.16) – параметрические уравнения прямой.
Пусть на прямой . (2.16)
(2.16) – параметрические уравнения прямой.
Пусть на прямой  заданы две точки заданы две точки  и и  . Тогда вектор . Тогда вектор  является направляющим вектором прямой и, используя уравнение (2.15), можно записать является направляющим вектором прямой и, используя уравнение (2.15), можно записать
 . (2.17)
(2.17) – уравнение прямой, проходящей через две данные точки.
Пусть . (2.17)
(2.17) – уравнение прямой, проходящей через две данные точки.
Пусть  – заданная точка на прямой – заданная точка на прямой  , ,  – угол наклона прямой к оси – угол наклона прямой к оси  , ,  (рис. 23). В качестве направляющего вектора прямой (рис. 23). В качестве направляющего вектора прямой  возьмем единичный вектор возьмем единичный вектор  . Координаты единичного вектора совпадают с его направляющими косинусами, поэтому . Координаты единичного вектора совпадают с его направляющими косинусами, поэтому  ,но ,но  . Используя уравнение (2.15), получим . Используя уравнение (2.15), получим  , или , или  . Обозначив . Обозначив  ( (  – угловой коэффициент прямой), получим уравнение – угловой коэффициент прямой), получим уравнение
 . (2.18) . (2.18)
 Рис. 23
Выразив из (2.18)
Рис. 23
Выразив из (2.18)  : :  и обозначив и обозначив  , получим , получим
 . (2.19)
(2.18), (2.19) – уравнения прямой с угловым коэффициентом. В уравнении (2.19) . (2.19)
(2.18), (2.19) – уравнения прямой с угловым коэффициентом. В уравнении (2.19)  – ордината точки пересечения прямой с осью – ордината точки пересечения прямой с осью  .
Угол между двумя прямыми. Пусть прямые .
Угол между двумя прямыми. Пусть прямые 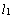 и и 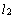 заданы соответственно уравнениями заданы соответственно уравнениями  , ,  , где , где  , ,  . Обозначим . Обозначим  угол между прямыми: угол между прямыми:  (рис. 24). Тогда (рис. 24). Тогда  , ,  . .
 Рис. 24
Таким образом,
Рис. 24
Таким образом,
 . (2.20)
Если . (2.20)
Если  , то , то  , а следовательно, , а следовательно,  , то есть k1= k2.
Если , то есть k1= k2.
Если  , то , то  , , 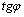 не определен, не определен,  , следовательно, , следовательно,  , или , или  .
Если прямые .
Если прямые 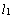 и и 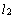 заданы соответственно уравнениями заданы соответственно уравнениями
 , ,  , где , где  , ,  – нормальные векторы прямых, то – нормальные векторы прямых, то 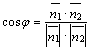 , или , или  .
Если .
Если  , то , то  , следовательно, , следовательно,  .
Если .
Если  , ,  , то есть , то есть  .
Расстояние от точки до прямой. Пусть прямая .
Расстояние от точки до прямой. Пусть прямая  на плоскости задана уравнением на плоскости задана уравнением  и точка и точка  имеет координаты имеет координаты 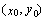 (рис. 25).
Обозначим (рис. 25).
Обозначим  – основание перпендикуляра, опущенного из точки – основание перпендикуляра, опущенного из точки  на прямую на прямую  , ,  , ,  – расстояние от точки – расстояние от точки  до прямой до прямой  . Тогда . Тогда 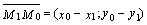 , а , а  – нормальный вектор прямой. Рассмотрим скалярное произведение – нормальный вектор прямой. Рассмотрим скалярное произведение  . С одной стороны, . С одной стороны,  , так как , так как  , следовательно, угол между ними , следовательно, угол между ними  или или  . С другой стороны, . С другой стороны,  , но точка , но точка  , поэтому ее координаты удовлетворяют уравнению , поэтому ее координаты удовлетворяют уравнению  , откуда , откуда  , поэтому , поэтому  . Приравнивая выражения, получим . Приравнивая выражения, получим
 . Тогда . Тогда  или или
 . (2.21) . (2.21)
 Рис. 25
Рис. 25
|
|
|
|
Билет 10.
|
|
|
Плоскость в пространстве. Различные формы уравнения плоскости. Простейшие задачи.
| Плоскость в пространстве | ||||||||
Пусть Мо(хо, уо, zо) – заданная точка в плоскости a,  = (А; В; С) – вектор, перпендикулярный плоскости a, его называют нормальным вектором плоскости, и пусть М(х, у, z) – произвольная точка плоскости (рис. 43). Тогда = (А; В; С) – вектор, перпендикулярный плоскости a, его называют нормальным вектором плоскости, и пусть М(х, у, z) – произвольная точка плоскости (рис. 43). Тогда   то есть то есть
(2.28) – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.
Рис. 43 Раскрыв скобки и сгруппировав слагаемые, получим
(2.29) – общее уравнение плоскости. Если в этом уравнении А, В, С, Д ¹ 0, то его можно привести к виду
(2.30) – уравнение плоскости в отрезках (аналогично (2.14)). Здесь а, в, с – отрезки, отсекаемые плоскостью на осях координат. Пусть заданы три точки в плоскости: М1(х1, у1, z1), М2(х2, у2, z2), М3(х3, у3, z3), и пусть М(х, у, z)–произвольная_точка_плоскости_(рис.44). Тогда
(2.31) – уравнение плоскости, проходящей через три данные точки.
Рис. 44 | ||||||||
| Неполные уравнения плоскостей | ||||||||
Если в уравнении плоскости  какие-либо из коэффициентов равны нулю, то получится неполное уравнение плоскости.
Пусть, например, какие-либо из коэффициентов равны нулю, то получится неполное уравнение плоскости.
Пусть, например,  Уравнение имеет вид Уравнение имеет вид  и определяет плоскость, проходящую через начало координат (координаты точки О(0; 0; 0) удовлетворяют уравнению).
Пусть и определяет плоскость, проходящую через начало координат (координаты точки О(0; 0; 0) удовлетворяют уравнению).
Пусть  Уравнение имеет вид Уравнение имеет вид  и определяет плоскость, параллельную оси Оz или проходящую через ось Оz при и определяет плоскость, параллельную оси Оz или проходящую через ось Оz при  Действительно, тогда Действительно, тогда  то есть то есть  а плоскость а плоскость  Пусть
Пусть  Уравнение имеет вид Уравнение имеет вид  и определяет плоскость, параллельную плоскости Оуz или совпадающую с ней при и определяет плоскость, параллельную плоскости Оуz или совпадающую с ней при  Действительно, Действительно,  то есть то есть  а плоскость а плоскость  или или  Аналогично можно рассмотреть другие случаи.
Аналогично можно рассмотреть другие случаи.
| ||||||||
| Угол между двумя плоскостями | ||||||||
Пусть плоскости a1 и a2 заданы соответственно уравнениями:

 где где   и и  – нормальные векторы этих плоскостей (рис. 45). Очевидно, – нормальные векторы этих плоскостей (рис. 45). Очевидно,  тогда косинус угла между плоскостями тогда косинус угла между плоскостями
Рис. 45
Если Если | ||||||||
Билет 11.
Нормальные уравнения прямой на плоскости и плоскости в пространстве. Отклонение точки от прямой (плоскости). Задачи решаемые с помощью отклонения.
|
|
|





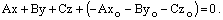 Обозначим
Обозначим 
 уравнение примет вид
уравнение примет вид



 Эти векторы компланарны (лежат в одной плоскости), следовательно, их смешанное произведение равно нулю:
Эти векторы компланарны (лежат в одной плоскости), следовательно, их смешанное произведение равно нулю:  или через координаты
или через координаты



 то
то  – условие параллельности плоскостей.
– условие параллельности плоскостей. то
то  то есть
то есть  – условие перпендикулярности плоскостей.
– условие перпендикулярности плоскостей.