 |
Основные свойства определителя
|
|
|
|
1. Равноправие строк и столбцов. При транспонировании матрицыее определитель не меняется.
2. Если все элементы какого-либо столбца (строки) определителя равны нулю, то определитель также равен нулю. Это свойство очевидно, так как каждое слагаемое содержит по одному и только одному сомножителю из каждого столбца (строки).
3. Антисимметрия. При перестановке двух любых столбцов (строк) определителя его знак меняется на противоположный, а абсолютная величина остается неизменной.
Доказательство свойств 1 и 3 основано на правиле расстановки знаков членов определителя.
Определитель с двумя одинаковыми столбцами (строками) равен нулю.
Действительно, при перестановке, например, двух одинаковых столбцов определитель не изменяется, но вместе с тем он в силу третьего свойства меняет знак на обратный, т. е.
, откуда 
или 
.
5. Линейность. Если j- й столбец 
(i -я строка A 
) определителя det A является линейной комбинацией A 
λ B + μ C (A λ B + μ C) двух произвольных столбцов (строк) В и С, то и сам определитель оказывается линейной комбинацией det A det A (λ B+ μ C) λdet A (B) + μ det A (C) определителей det A (B) и detA (C). Здесь det A (B) (det A (C)) – определитель, полученный из определителя det А заменой в нем j -го столбца A на столбец В(столбец С).
6. Общий множитель всех элементов какого-либо столбца (строки) определителя можно вынести за его знак. Отсюда следует, что если какой-либо столбец (строку) определителя умножить на число λ, то сам определитель умножится на это число.
Если какой-либо столбец (строка) определителя является линейной комбинацией других его столбцов (строк), то определитель равен нулю.
Свойства 6 и 7 вытекают из пятого свойства.
|
|
|
Определитель не изменится, если к любому его столбцу (строке) прибавить произвольную линейную комбинацию его столбцов (строк).
Действительно, в силу линейности определитель равен сумме исходного определителя и определителя с двумя одинаковыми столбцами (строками).
9. Определитель суммы двух квадратных матриц одного и того же порядка n A 
и В 
, i, j = 
равен сумме всех различных определителей порядка n, которые могут получиться, если часть строк (столбцов) брать совпадающими с соответствующими строками (столбцами) матрицы А, а оставшуюся часть – совпадающими с соответствующими строками (столбцами) матрицы В.
Доказательство следует из свойства линейности определителя.
10. Определитель произведения двух матриц равен произведению их определителей det (AВ) det A×det B.
Билет 30.
Дополнительный минор элемента определителя и алгебраическое дополнение. Теорема о разложении определителя по столбцу (строке).
Дополнительный минор 
квадратной матрицы 
порядка 
(
) — определитель матрицы, полученной из исходной вычеркиванием 
строк и 
столбцов.
Иногда дополнительным минором называют не определитель, а саму матрицу, полученную из исходной вышеуказанным способом.
Дополнительный минор произвольного элемента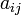 
квадратной матрицы — дополнительный минор 
. Каждый элемент квадратной матрицы имеет свой дополнительный минор.
Имеет место разложение по строке:
Определитель матрицы равен 
, где 
— дополнительный минор к элементу 
.
Алгебраическим дополнением элемента 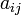матрицы называется число
,
где 
— дополнительный минор, определитель матрицы, получающейся из исходной матрицы путем вычёркивания i -й строки и j -го столбца.
Свойства
Название «алгебраическое дополнение» связано с формулами разложения определителя матрицы по строке (по столбцу):
|
|
|
